MengerMesh[n]
gives a mesh region representing the n![]() -step Menger sponge.
-step Menger sponge.
MengerMesh[n,d]
gives the n![]() -step Menger sponge in dimension d.
-step Menger sponge in dimension d.




MengerMesh
MengerMesh[n]
gives a mesh region representing the n![]() -step Menger sponge.
-step Menger sponge.
MengerMesh[n,d]
gives the n![]() -step Menger sponge in dimension d.
-step Menger sponge in dimension d.
Details and Options

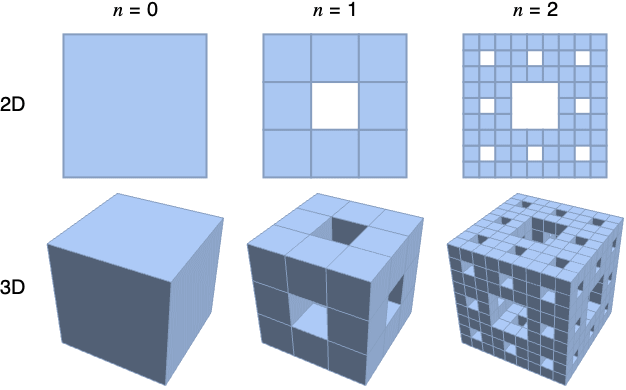
- MengerMesh is also known as Sierpiński carpet.
- MengerMesh[n] is generated from a unit square by repeatedly removing the middle square of the subsequent cells. »
- MengerMesh[n] is equivalent to MengerMesh[n,2].
- MengerMesh takes the same options as MeshRegion, with the following additions:
-
DataRange Automatic the range of mesh coordinates to generate
Examples
open all close allBasic Examples (2)
Options (12)
DataRange (1)
DataRange allows you to specify the range of mesh coordinates to generate:
MeshCellHighlight (2)
MeshCellHighlight allows you to specify highlighting for parts of a MengerMesh:
Individual cells can be highlighted using their cell indices:
MeshCellLabel (2)
MeshCellLabel can be used to label parts of a MengerMesh:
MeshCellMarker (1)
MeshCellMarker can be used to assign values to parts of a MengerMesh:
Use MeshCellLabel to show the markers:
MeshCellShapeFunction (2)
MeshCellShapeFunction can be used to assign values to parts of a MengerMesh:
MeshCellStyle (2)
MeshCellStyle allows you to specify styling for parts of a MengerMesh:
Individual cells can be highlighted using their cell indices:
Applications (1)
Properties & Relations (7)
The output of MengerMesh is always a full-dimensional MeshRegion:
MengerMesh consists of rectangles in 2D:
Find the area of the Menger mesh in 2D at each stage:
Find the volume of the Menger mesh in 3D at each stage:
Each face of the MengerMesh in 3D (Menger sponge) is a MengerMesh in 2D (Sierpiński carpet):
Find the boundary mesh region of MengerMesh:
DataRange->range is equivalent to using RescalingTransform[{...},range]:
Use RescalingTransform:
Possible Issues (1)
MengerMesh can be too large to generate:
Related Guides
History
Text
Wolfram Research (2017), MengerMesh, Wolfram Language function, https://reference.wolfram.com/language/ref/MengerMesh.html.
CMS
Wolfram Language. 2017. "MengerMesh." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MengerMesh.html.
APA
Wolfram Language. (2017). MengerMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MengerMesh.html
BibTeX
@misc{reference.wolfram_2025_mengermesh, author="Wolfram Research", title="{MengerMesh}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/MengerMesh.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_mengermesh, organization={Wolfram Research}, title={MengerMesh}, year={2017}, url={https://reference.wolfram.com/language/ref/MengerMesh.html}, note=[Accessed: 06-February-2026]}