Minors
更多信息

- 对一个
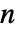 ×
×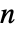 矩阵,Minors[m] 的
矩阵,Minors[m] 的 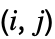 元素为去掉 m 的第
元素为去掉 m 的第 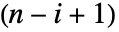 行和第
行和第 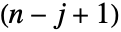 列后得到的矩阵的行列式. »
列后得到的矩阵的行列式. » - Reverse[Minors[m],{1,2}] 使得第
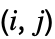
 个元素对应删除矩阵 m 的第
个元素对应删除矩阵 m 的第 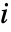
 行和第
行和第 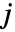
 列. »
列. » - Minors[m] 等价于 Minors[m,Min[Dimensions[m]]-1]. »
- Minors[m,k] 给出通过从 m 中选取每组可能的 k 行和 k 列得到的 k×k 子矩阵的行列式.
- 结果中的每个元素对应于在特定位置列表选取的行和列. 元素的排序方式是使得在读出最后矩阵时,连续位置列表具有按字典排序的方式.
- 对于一个
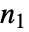 ×
×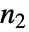 矩阵,Minors[m,k] 给出一个
矩阵,Minors[m,k] 给出一个 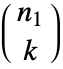 ×
×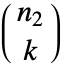 矩阵.
矩阵.
范例
打开所有单元关闭所有单元范围 (14)
指定子式大小 (4)
特殊矩阵 (4)
应用 (5)
可视化用来计算方阵的 Minors[m] 的行列式:
从两个层级上反向排列 m,获取删除第 ![]() 行和第
行和第 ![]() 列后得到第
列后得到第 ![]()
![]() 项元素:
项元素:
与 Adjugate 返回的结果相比较:
阶是满足 Minors[mat,k] 包含非零项的最大 k:
用 MatrixRank 检测这个阶等于 2:
用 Sylvester 标准测试 Hermitian 矩阵是否为正定矩阵:
由于所有的顺序主子式 (leading principle minor) 都是正的,所以矩阵是正定的:
用 PositiveDefiniteMatrixQ 确认结果:
属性和关系 (11)
对于一个 ![]() 矩阵,Minors[m] 是通过删除第
矩阵,Minors[m] 是通过删除第 ![]() 行和第
行和第 ![]() 列得到的行列式矩阵:
列得到的行列式矩阵:
Reverse[Minors[m],{1,2}] 是通过删除 m 的第 ![]() 行和第
行和第 ![]() 列得到的行列式矩阵:
列得到的行列式矩阵:
当 r=Reverse[Minors[m],{1,2}] 时,可以表达为 ![]() :
:
Minors[m] 等价于 Minors[m]==Minors[m,Min[Dimensions[m]]-1]:
对于方阵 m,Minors[m,Length[m]] 等于 {{Det[m]}}:
根据定义,Minors[m,0] 即是 {{1}}:
维数高于 MatrixRank 的 Minors 为零:
一个 ![]() ×
×![]() 矩阵的
矩阵的 ![]() 次子式的 Dimensions 是
次子式的 Dimensions 是 ![]() ×
×![]() :
:
方阵的 Minors 为另一个单位矩阵:
方形对角矩阵的 Minors 为另一个对角矩阵:
Minors 等价于从矩阵中提取的行和列的外积:
文本
Wolfram Research (1988),Minors,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Minors.html (更新于 2022 年).
CMS
Wolfram 语言. 1988. "Minors." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2022. https://reference.wolfram.com/language/ref/Minors.html.
APA
Wolfram 语言. (1988). Minors. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Minors.html 年