ModularLambda

ModularLambda[τ]

モジュラ・ラムダ楕円関数 TemplateBox[{tau}, ModularLambda]を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • ModularLambdaは，複素 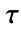平面の上半平面において定義される．実数 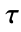に対しては定義されない．
  • 引数 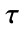はワイエルシュトラスの半周期の比 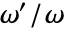である．
  • ModularLambdaは，楕円関数に対して，m=TemplateBox[{tau}, ModularLambda]に従った 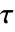によるパラメータ 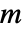を与える．
  • ModularLambdaは，式 TemplateBox[{tau}, ModularLambda]=TemplateBox[{2, 0, q}, EllipticTheta]^4/TemplateBox[{3, 0, q}, EllipticTheta]^4を介しEllipticThetaに関連している．ただし，ノーム 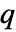は 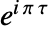で与えられるものとする．
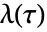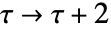  • は，と 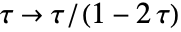のモジュラ変換のいかなる組合せにおいても不変である． »
  • 特別な引数の場合，ModularLambdaは，自動的に厳密値を計算する．
  • ModularLambdaは任意の数値精度で評価できる．
  • ModularLambdaはCenteredIntervalオブジェクトに使うことができる． »
  • ModularLambdaは自動的にりストに縫い込まれる． »

例題

すべて開くすべて閉じる

例  (3)

数値的に評価する：

実数の部分集合上でプロットする：

原点における級数展開：

スコープ  (23)

数値評価  (5)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

高精度で効率的に評価する：

自動縫込みを使って配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のModularLambda関数を計算することもできる：

ModularLambdaはCenteredIntervalオブジェクトに使うことができる：

特定の値  (2)

固定点における値：

ModularLambda[x+I]の最初の正の最小値を求める：

可視化  (3)

ModularLambdaの実部をプロットする：

ModularLambdaの絶対値をプロットする：

ModularLambda関数の実部をプロットする：

ModularLambda関数の虚部をプロットする：

関数の特性  (9)

ModularLambdaは上半平面で定義される：

ModularLambdaは周期関数である：

ModularLambdaは要素単位でリストに縫い込まれる：

ModularLambdaはその定義域上で解析関数である：

したがって，そこでは特異点と不連続点のどちらも持たない：

Re(TemplateBox[{{x, +, ⅈ}}, ModularLambda])は非減少でも非増加でもない：

Re(TemplateBox[{{x, +, ⅈ}}, ModularLambda])は単射ではない：

Re(TemplateBox[{{x, +, ⅈ}}, ModularLambda])は非負でも非正でもない：

Re(TemplateBox[{{x, +, ⅈ}}, ModularLambda])は凸でも凹でもない：

TraditionalFormによる表示：

微分  (2)

z についての一次導関数：

z についての高次導関数：

z についての高次導関数をプロットする：

級数展開  (2)

Seriesを使ってテイラー(Taylor)展開を求める：

の周りの最初の3つの近似をプロットする：

生成点におけるテイラー展開：

アプリケーション  (4)

ModularLambdaのモジュラ属性の中には自動的に適用されるものがある：

より複雑な恒等式を数値的に証明する：

ModularLambdaはモジュラ関数である．モジュラ方程式のansatzを作る：

方程式の過剰決定系を作り，これを解く：

これは二次のモジュラ方程式である：

Darboux–Halphen系の解：

検証する：

複素平面上で実部をプロットする：

特性と関係  (2)

導関数を求める：

数値根を求める：

考えられる問題  (2)

機械精度の入力では正しい答を得るには不十分である：

厳密な入力だと正しい答が得られる：

ModularLambdaは解析性の領域外では未評価のまま残される：

Wolfram Research (1996), ModularLambda, Wolfram言語関数， https://reference.wolfram.com/language/ref/ModularLambda.html （2021年に更新）.

テキスト

Wolfram Research (1996), ModularLambda, Wolfram言語関数， https://reference.wolfram.com/language/ref/ModularLambda.html （2021年に更新）.

CMS

Wolfram Language. 1996. "ModularLambda." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ModularLambda.html.

APA

Wolfram Language. (1996). ModularLambda. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ModularLambda.html

BibTeX

@misc{reference.wolfram_2024_modularlambda, author="Wolfram Research", title="{ModularLambda}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/ModularLambda.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_modularlambda, organization={Wolfram Research}, title={ModularLambda}, year={2021}, url={https://reference.wolfram.com/language/ref/ModularLambda.html}, note=[Accessed: 21-November-2024 ]}