Modulus
Modulusn
is an option that can be given in certain algebraic functions to specify that integers should be treated modulo n.
Details
- Modulus appears as an option in Solve, Reduce, Factor, PolynomialGCD, and PolynomialLCM, as well as in linear algebra functions such as Inverse, LinearSolve, and Det.
- Arithmetic is usually done over the full ring
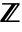 of integers; setting the option Modulus specifies that arithmetic should instead be done in the finite ring
of integers; setting the option Modulus specifies that arithmetic should instead be done in the finite ring 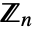 .
. - The setting Modulus->0 specifies the full ring
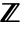 of integers.
of integers. - Some functions require that Modulus be set to a prime, or a power of a prime.
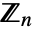 is a finite field when
is a finite field when 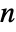 is prime.
is prime. - Equations for Modulus can be given in Eliminate and related functions.
Examples
open allclose allScope (6)
Compute PolynomialGCD over the integers modulo 2:
Factor a polynomial over the integers modulo 3:
Find a GroebnerBasis over the integers modulo 5:
Reduce equations over the integers modulo 7:
Compute the determinant of a matrix modulo 8:
Find a modulus for which a system of equations has a solution:
Text
Wolfram Research (1988), Modulus, Wolfram Language function, https://reference.wolfram.com/language/ref/Modulus.html.
CMS
Wolfram Language. 1988. "Modulus." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Modulus.html.
APA
Wolfram Language. (1988). Modulus. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Modulus.html