

OrderedQ
Details

- OrderedQ[{e,e}] gives True.
- By default, OrderedQ uses canonical order as described in the notes for Sort. This is equivalent to specifying Order as the ordering function p. »
- The ordering function p applied to a pair of elements e1, e2 may return either 1, 0,
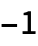 or True, False. The value of p[e1,e2] is interpreted as follows:
or True, False. The value of p[e1,e2] is interpreted as follows: -
1 e1 comes before e2 0 e1 and e2 should be treated as identical -1 e1 comes after e2 True e1 and e2 are in order False e1 and e2 are out of order - If the ordering function p returns a value p[e1,e2] other than the preceding ones, then e1 and e2 are effectively treated as being in order. »
Examples
open all close allBasic Examples (4)
Scope (8)
OrderedQ works with any expression:
OrderedQ works with any head, not just List:
Check whether the values of an association are in order:
Specify Greater as the ordering function:
Use GreaterEqual to allow repeated elements:
Use NumericalOrder to allow complex numbers and number-like expressions:
Sort according to the rules of a particular language with AlphabeticOrder:
Define a custom ordering function that puts symbols ahead of numbers:
Properties & Relations (7)
OrderedQ[expr] is equivalent to OrderedQ[expr,Order]:
Comparisons are stopped as soon as it is determined that a pair is out of order:
For explicit numbers, OrderedQ is effectively equivalent to LessEqual:
For any association, OrderedQ[assoc,…]==OrderedQ[Values[assoc],…]:
OrderedQ[expr] gives True when Sort[expr]===expr:
Sort by default effectively sorts using OrderedQ:
OrderedQ uses non-strict order by default:
Check for strict canonical order by adding UnsameQ to the ordering function:
Alternatively, check whether Order gives 1:
Possible Issues (2)
OrderedQ by default works structurally, not by numerical value:
Numericize elements or use NumericalOrder to compare by numerical value:
Unrecognized values of the ordering function are interpreted as elements being in order:
Use TrueQ to interpret failed comparisons as being out of order:
Tech Notes
Related Guides
History
Introduced in 1988 (1.0) | Updated in 2017 (11.1)
Text
Wolfram Research (1988), OrderedQ, Wolfram Language function, https://reference.wolfram.com/language/ref/OrderedQ.html (updated 2017).
CMS
Wolfram Language. 1988. "OrderedQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/OrderedQ.html.
APA
Wolfram Language. (1988). OrderedQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/OrderedQ.html
BibTeX
@misc{reference.wolfram_2025_orderedq, author="Wolfram Research", title="{OrderedQ}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/OrderedQ.html}", note=[Accessed: 23-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_orderedq, organization={Wolfram Research}, title={OrderedQ}, year={2017}, url={https://reference.wolfram.com/language/ref/OrderedQ.html}, note=[Accessed: 23-January-2026]}