UnsameQ

lhs=!=rhs

yields True if the expression lhs is not identical to rhs, and yields False otherwise.

Details

Background & Context

  • UnsameQ[expr1,expr2] returns True if expr1 is not identical expr2 and otherwise returns False. In particular, UnsameQ[expr1,expr2] returns False if and only if SameQ[expr1,expr2] returns True (i.e. if there is exact correspondence between the underlying FullForm representations of expressions expr1 and expr2, with the exception that real numbers are considered SameQ if they differ only in their last binary digit). UnsameQ[expr1,expr2] may be input as expr1=!=expr2. The multiple-argument form UnsameQ[expr1,expr2,…], which may also be input as expr1=!=expr2=!=…, returns True if no two of the expressions expri are identical.
  • Different input forms of expressions will not be UnsameQ if their underlying representations are identical; for example, n! =!=Factorial[n] returns False. On the other hand, UnsameQ differentiates between representations of numbers that are numerically equal but that do not have identical representations. For example, UnsameQ[1,1.] and UnsameQ[1.,1.+0.I] both return True. This behavior is expressly different from that exhibited by Unequal, which performs equality testing and remains unevaluated in cases that cannot be resolved.
  • UnsameQ is related to a number of other symbols. Unequal[expr1,expr2] (which may be input as expr1!=expr2 or expr1≠expr2) returns True if expr1 and expr2 are numerically unequal. SameQ (which may be input as expr1===expr2) is the converse of UnsameQ.
  • PossibleZeroQ can be used to indicate if a given expression has value 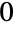in some cases where UnsameQ returns True. For example, UnsameQ[Erf[Log[4]+2Log[Sin[Pi/8]]]-Erf[Log[2-Sqrt[2]]],0] returns True, whereas calling PossibleZeroQ on its first argument indicates it is equal to zero by returning True (together with an informative message indicating that a zero value could not be rigorously established). Symbolic simplifiers like Simplify, FullSimplify and RootReduce can sometimes also be used to rigorously establish equality (including in the example just given) when UnsameQ and Unequal (or SameQ and Equal) cannot.

Examples

open allclose all

Basic Examples  (2)

Test whether two expressions are not identically the same:

!= remains symbolic unless literal values are given:

Full form:

Scope  (3)

Test equivalence of strings:

Numbers in different representations are not the same:

!= nevertheless treats them as equal:

Test whether multiple expressions are all distinct:

Applications  (1)

Construct the permanent analog of the totally antisymmetric tensor:

1 appears at positions corresponding to permutations:

Properties & Relations  (4)

UnsameQ accepts any number of arguments:

UnsameQ[expr1,expr2,…] gives True if UnsameQ[expri,exprj] is True for all i and j:

If one of the expressions is the same as another, then UnsameQ gives False:

UnsameQ[expr1,expre2] is equivalent to !SameQ[expr1,expr2]:

UnsameQ[…] and !SameQ[…] are not equivalent for an argument count other than two:

UnsameQ[] and UnsameQ[expr] always give True:

Wolfram Research (1991), UnsameQ, Wolfram Language function, https://reference.wolfram.com/language/ref/UnsameQ.html.

Text

Wolfram Research (1991), UnsameQ, Wolfram Language function, https://reference.wolfram.com/language/ref/UnsameQ.html.

CMS

Wolfram Language. 1991. "UnsameQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/UnsameQ.html.

APA

Wolfram Language. (1991). UnsameQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/UnsameQ.html

BibTeX

@misc{reference.wolfram_2024_unsameq, author="Wolfram Research", title="{UnsameQ}", year="1991", howpublished="\url{https://reference.wolfram.com/language/ref/UnsameQ.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_unsameq, organization={Wolfram Research}, title={UnsameQ}, year={1991}, url={https://reference.wolfram.com/language/ref/UnsameQ.html}, note=[Accessed: 21-November-2024 ]}