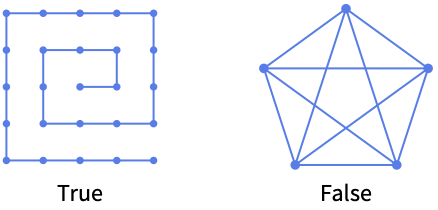
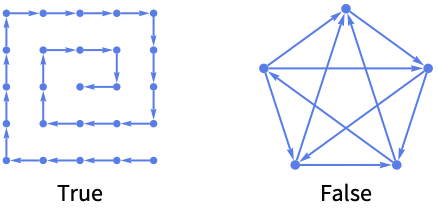
PathGraphQ

PathGraphQ[g]

yields True if the graph g is a path and False otherwise.

Details

  • An undirected path graph is a connected graph where each vertex has at most degree two.
  • A directed path graph is a connected graph where each vertex has at most in-degree one and at most out-degree one.

Examples

open allclose all

Basic Examples  (2)

Test whether a graph is a path:

The vertex degree is at most 2:

A complete graph is not a path:

The vertex degree is greater than 2:

Scope  (6)

PathGraphQ works with undirected graphs:

Directed graphs:

Multigraphs:

Mixed graphs:

PathGraphQ gives False for anything that is not a path graph:

Test large graphs:

Properties & Relations  (8)

A path graph is loop-free if it has more than one vertex:

A path graph does not necessarily have edges:

A path graph that starts and ends in the same vertex is a cycle graph:

A path graph with no repeated vertices is a tree:

An acyclic path graph is simple:

And also bipartite:

GridGraph[{1,…,1,k,1,…,1}] are all path graphs:

A path graph is connected and each vertex has at most degree 2:

The line graph of a path is isomorphic to :

Possible Issues  (1)

PathGraphQ gives False for non-explicit graphs:

Wolfram Research (2010), PathGraphQ, Wolfram Language function, https://reference.wolfram.com/language/ref/PathGraphQ.html.

Text

Wolfram Research (2010), PathGraphQ, Wolfram Language function, https://reference.wolfram.com/language/ref/PathGraphQ.html.

CMS

Wolfram Language. 2010. "PathGraphQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PathGraphQ.html.

APA

Wolfram Language. (2010). PathGraphQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PathGraphQ.html

BibTeX

@misc{reference.wolfram_2024_pathgraphq, author="Wolfram Research", title="{PathGraphQ}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PathGraphQ.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_pathgraphq, organization={Wolfram Research}, title={PathGraphQ}, year={2010}, url={https://reference.wolfram.com/language/ref/PathGraphQ.html}, note=[Accessed: 21-November-2024 ]}