WOLFRAM

Wolfram Language & System Documentation Center

PhaseMargins[lsys]

gives the phase margins of the linear time-invariant system lsys.

Details and Options
Details and Options Details and Options
Examples  
Basic Examples  
Generalizations & Extensions  
Properties & Relations  
See Also
Related Guides
History
Cite this Page

PhaseMargins

PhaseMargins[lsys]

gives the phase margins of the linear time-invariant system lsys.

Details and Options

  • The system lsys can be a TransferFunctionModel or a StateSpaceModel.
  • The phase margins are phase lags needed to make the phase 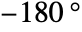at the gain crossover frequencies.
  • At the gain crossover frequencies, the gain of lsys is unity.
  • PhaseMargins returns {{ωg1,p1},{ωg2,p2},…}, where ωgi are the gain crossover frequencies, and pi are the phase margins in radians.
  • PhaseMargins has the same options as GainPhaseMargins.
  • PhaseMargins has the attribute Listable.

    • List of all options

Examples

open all close all

Basic Examples  (4)

The phase margins of a continuous-time system:

The phase margin in degrees:

A discrete-time system:

A system specified as a transfer-function model:

A time-delay system:

Generalizations & Extensions  (1)

PhaseMargins[TransferFunctionModel[g,var]] is equivalent to PhaseMargins[g]:

Properties & Relations  (1)

The phase margin increases with damping:

A plot of the phase margin as the damping increases:

Wolfram Research (2010), PhaseMargins, Wolfram Language function, https://reference.wolfram.com/language/ref/PhaseMargins.html.

Text

Wolfram Research (2010), PhaseMargins, Wolfram Language function, https://reference.wolfram.com/language/ref/PhaseMargins.html.

CMS

Wolfram Language. 2010. "PhaseMargins." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PhaseMargins.html.

APA

Wolfram Language. (2010). PhaseMargins. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PhaseMargins.html

BibTeX

@misc{reference.wolfram_2025_phasemargins, author="Wolfram Research", title="{PhaseMargins}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PhaseMargins.html}", note=[Accessed: 15-August-2025]}

BibLaTeX

@online{reference.wolfram_2025_phasemargins, organization={Wolfram Research}, title={PhaseMargins}, year={2010}, url={https://reference.wolfram.com/language/ref/PhaseMargins.html}, note=[Accessed: 15-August-2025]}