PhaseMargins

PhaseMargins[lsys]

線形時不変系 lsys の位相余裕を与える．

詳細とオプション

  • 系 lsys はTransferFunctionModelあるいはStateSpaceModelである．
  • 位相余裕は，ゲイン交差周波数で位相を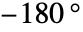にするのに必要な位相遅れである．
  • ゲイン交差周波数で lsys のゲインは単位元である．
  • PhaseMarginsは{{ωg1,p1},{ωg2,p2},…}を返す．ただし，ωgi はゲイン交差周波数であり，pi は位相余裕（ラジアン）である．
  • PhaseMarginsにはGainPhaseMarginsと同じオプションが使える．
  • PhaseMarginsは属性Listableを有する．

    • 全オプションのリスト

例題

すべて開くすべて閉じる

例  (4)

連続時間系の位相余裕：

位相余裕を度で：

離散時間系：

伝達関数モデルとして指定された系：

時間遅延系：

一般化と拡張  (1)

PhaseMargins[TransferFunctionModel[g,var]]はPhaseMargins[g]と等価である：

特性と関係  (1)

位相余裕は減衰とともに増加する：

Wolfram Research (2010), PhaseMargins, Wolfram言語関数， https://reference.wolfram.com/language/ref/PhaseMargins.html.

テキスト

Wolfram Research (2010), PhaseMargins, Wolfram言語関数， https://reference.wolfram.com/language/ref/PhaseMargins.html.

CMS

Wolfram Language. 2010. "PhaseMargins." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PhaseMargins.html.

APA

Wolfram Language. (2010). PhaseMargins. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PhaseMargins.html

BibTeX

@misc{reference.wolfram_2024_phasemargins, author="Wolfram Research", title="{PhaseMargins}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PhaseMargins.html}", note=[Accessed: 03-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_phasemargins, organization={Wolfram Research}, title={PhaseMargins}, year={2010}, url={https://reference.wolfram.com/language/ref/PhaseMargins.html}, note=[Accessed: 03-December-2024 ]}