Pi

Pi

円周率 を表し，その数値は約である．

詳細

  • NumericQには数値として，Dには定数として扱われる数学定数である．
  • PiはNを使って任意精度で評価できる．
  • PiはStandardFormやInputFormで，π，pi，p，\[Pi]と入力できる．
  • StandardFormでは，Piは π と表示される．

予備知識

  • Piは，数学定数 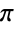を表す記号である．これは，∖[Pi]としても入力できる．Piは，円周の直径に対する比として定義され，数値ではと表す．Piは，三角法の式，特殊関数の値，和，積，積分の数学的計算，さまざまな数学と科学の分野における式に現れる．
  • Piは，記号として使われた場合は厳密な数量として伝えられる．Piを含む多くの式（例：Cos[Pi/10]）は，自動的により単純な関数に展開されるが，Piを含むより複雑な式（例：Cos[Pi/15]）の展開と簡約にはFunctionExpandやFullSimplifyのような関数の使用が必要なことがある．
  • Piは無理かつ超越的である，すなわち整数の比としても任意の整数多項式の根としても表すことができないとして知られている．Piが任意の基底について正規数（基底 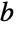の展開による各桁の数字が均等に分布している）かどうかは未知であるが，既知の各桁の数字は非常に一様に分布している．
  • Piは，Nを使ったChudnovsky公式を通して，任意数値精度に評価することができる．実際，最新のデスクトップコンピュータを使うと，Piの最初の100万桁も1秒かからずに計算することができる．RealDigitsを使ってPiの各桁の数字を返したり，ContinuedFractionを使って連分数展開の項を得たりすることができる．
  • Wolfram言語で角度に関する関数のほとんどは，その引数にラジアンの測定値を取り，結果としてラジアン値を返す．このため記号Degree（Pi/180に等しい）は，角度の測定値（例：Cos[30 Degree]）を入力する際には，乗数として使うことができる．

例題

すべて開くすべて閉じる

例  (3)

パイはpで入力できる：

任意の精度まで評価する：

厳密な数値計算を行う：

スコープ  (1)

10を底とした の100万桁目の数字を求める：

アプリケーション  (5)

円の面積を求める：

底10での の最初の20桁：

三角関数の引数はラジアンである：

を含む結果を返す数学関数や演算はたくさんある：

特性と関係  (2)

さまざまな記号関係が自動的に使われる：

Piは微分で定数として扱われる：

おもしろい例題  (2)

π のバイナリ桁数に呼応したウォーク：

連分数の項：

Wolfram Research (1988), Pi, Wolfram言語関数， https://reference.wolfram.com/language/ref/Pi.html （1996年に更新）.

テキスト

Wolfram Research (1988), Pi, Wolfram言語関数， https://reference.wolfram.com/language/ref/Pi.html （1996年に更新）.

CMS

Wolfram Language. 1988. "Pi." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/Pi.html.

APA

Wolfram Language. (1988). Pi. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Pi.html

BibTeX

@misc{reference.wolfram_2024_pi, author="Wolfram Research", title="{Pi}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Pi.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_pi, organization={Wolfram Research}, title={Pi}, year={1996}, url={https://reference.wolfram.com/language/ref/Pi.html}, note=[Accessed: 21-November-2024 ]}