PowerSymmetricPolynomial
指数が r の形式的なベキ対称式を表す.
PowerSymmetricPolynomial[{r1,r2,…}]
指数が r1, r2, … の多変量の形式的なベキ対称式を表す.
PowerSymmetricPolynomial[rspec,data]
data におけるベキ対称式を返す.
詳細
- PowerSymmetricPolynomial[r,{x1,x2,…,xn}]は
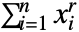 によって与えられる.
によって与えられる. - PowerSymmetricPolynomial[{r1,r2,…},{{x11,x12,…},…,{xn 1,xn 2,…}}]は
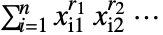 によって与えられる.
によって与えられる. - PowerSymmetricPolynomial[rspec]を使ってモーメント推定で使われる形式的なベキ和を表すことができる.
- MomentConvertを使ってPowerSymmetricPolynomialオブジェクトによるモーメント推定量を生成することができる.
- MomentEvaluateを使ってデータ集合についての形式的なPowerSymmetricPolynomialオブジェクトについての多項式を評価することができる.
例題
すべて開くすべて閉じる例 (1)
スコープ (3)
位数0のPowerSymmetricPolynomialは事実上データ点の数である:
MomentEvaluateを使ってデータについての形式的なベキ対称式を評価する:
TraditionalFormによる表示:
アプリケーション (1)
AugmentedSymmetricPolynomialを使ってベキ対称式を線形化する:
特性と関係 (1)
PowerSymmetricPolynomial は1個の指数の場合, AugmentedSymmetricPolynomial と同じである:
テキスト
Wolfram Research (2010), PowerSymmetricPolynomial, Wolfram言語関数, https://reference.wolfram.com/language/ref/PowerSymmetricPolynomial.html.
CMS
Wolfram Language. 2010. "PowerSymmetricPolynomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PowerSymmetricPolynomial.html.
APA
Wolfram Language. (2010). PowerSymmetricPolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PowerSymmetricPolynomial.html