ProductLog

ProductLog[z]

における w の主要解を与える．

ProductLog[k,z]

第 k 解を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • 複数ある解は虚部の順に並べられる．
  • のとき，ProductLog[z]は実数である．
  • ProductLog[z]は，微分方程式 を満たす．
  • 特別な引数の場合，ProductLogは自動的に厳密値を計算する．
  • ProductLogは任意の数値精度で評価できる．
  • ProductLogは自動的にリストに縫い込まれる． »
  • ProductLog[z]は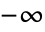，と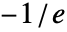 の間の複素平面 z に分枝切断線を持つ．
  • ProductLog[k,z]の k は 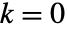が主要解に相当するような整数でよい．
  • ProductLog[k,z]は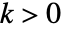，なる整数に対して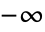，と0の間に分枝切断線を持つ．
  • ProductLogはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例  (6)

数値的に評価する：

実数の部分集合上でプロットする：

複素数の部分集合上でプロットする：

原点における級数展開：

Infinityにおける漸近展開：

特異点における漸近展開：

スコープ  (36)

数値評価  (6)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素数入力：

高精度で効率的に評価する：

自動縫込みを使って配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のProductLog関数を計算することもできる：

ProductLogはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる：

特定の値  (4)

固定点におけるProductLogの値：

ゼロにおける値：

無限大における値：

FindRootを使ってProductLog[x]=0.5となるような x の値を求める：

可視化  (3)

ProductLog関数をプロットする：

の実部をプロットする：

の虚部をプロットする：

による極プロット：

関数の特性  (10)

ProductLogは，区間[-,∞)からのすべての実数値について定義される：

ProductLogは，すべての複素値について定義される：

2引数の形のでは は整数で でなければならない：

実数範囲：

ProductLogは解析関数ではない：

有理型でもない：

ProductLogは実領域で増加する：

ProductLogは単射である：

ProductLogは全射ではない：

ProductLogは非負でも非正でもない：

ProductLogは(-∞,-]に特異点と不連続点の両方を持つ：

ProductLogは実領域で凹である：

TraditionalFormによる表示：

微分  (3)

z についての一次導関数：

z についての高次導関数：

高次導関数を z についてプロットする：

ネストした対数関数の導関数：

積分  (3)

Integrateを使って不定積分を計算する：

不定積分を確かめる：

ProductLogの定積分：

その他の積分例：

級数展開  (5)

Seriesを使ってテイラー(Taylor)展開を求める：

の周りの最初の3つの近似のプロット：

2引数形式を展開する：

SeriesCoefficientを使った級数展開の一般項：

Infinityにおける級数展開を求める：

分岐点と分枝切断線における級数展開を求める：

無限大における級数展開はネストした対数を含んでいる：

関数の恒等式と簡約  (2)

ProductLogは，以下の方程式の解を与える：

実変数 x および y を仮定して展開する：

一般化と拡張  (3)

異なるリーマン面において数値的に評価する：

分岐点と分枝切断線における級数展開を求める：

では分岐点と分枝切断線が異なる：

アプリケーション  (11)

方程式をProductLogを使って解く：

ProductLogの実部と虚部をプロットする：

ProductLogのリーマン面をプロットする：

の極限を計算する：

の明示的な反復と厳密な結果とを比較する：

母関数からラベルの付いた根のない木の数を判断する：

ロトカ・ヴォルテラ(Lotka–Volterra)方程式を解く：

Planckの黒体のスペクトルの最高値の周波数を求める：

Haissinski方程式を解く：

マッチが点けられると，結果の炎の球は半径 から始まって特定のサイズになっるまで急速に大きくな理，その後その大きさを保つ．これは，炎の球の中で燃焼によって消費される酸素と表面からの供給量とのバランスが取れるからである．炎の伝播をモデル化する関数を定義する：

この関数が単純な非線形微分方程式を満足することを示す：

簡約された炎の伝播モデルを の範囲で可視化する．になるまで徐々に大きくなり，短期間の急速な成長の後徐々に減少することが分かる：

平板コンデンサの等電位曲線：

Gram pointsを計算する：

連続する点でRiemannSiegelZの符号が変わる，よいGram pointを示す：

悪いGram pointを示す：

特性と関係  (5)

ProductLogは の逆関数である：

逆関数を使った構成にはPowerExpandが必要かもしれない：

FullSimplifyを使ってProductLogを含む式を簡約する：

超越関数を解く：

積分：

考えられる問題  (2)

一般に である：

分枝切断線上では，機械精度の入力では誤った答が与えられることがある：

任意精度演算を使って正しい結果を得る：

おもしろい例題  (2)

ネストした導関数：

ネストした積分：

Wolfram Research (1996), ProductLog, Wolfram言語関数， https://reference.wolfram.com/language/ref/ProductLog.html （2022年に更新）.

テキスト

Wolfram Research (1996), ProductLog, Wolfram言語関数， https://reference.wolfram.com/language/ref/ProductLog.html （2022年に更新）.

CMS

Wolfram Language. 1996. "ProductLog." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/ProductLog.html.

APA

Wolfram Language. (1996). ProductLog. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ProductLog.html

BibTeX

@misc{reference.wolfram_2024_productlog, author="Wolfram Research", title="{ProductLog}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ProductLog.html}", note=[Accessed: 20-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_productlog, organization={Wolfram Research}, title={ProductLog}, year={2022}, url={https://reference.wolfram.com/language/ref/ProductLog.html}, note=[Accessed: 20-November-2024 ]}