ProductLog
ProductLog[z]
给出 ![]() 关于 w 的主解.
关于 w 的主解.
ProductLog[k,z]
给出第 k![]() 个解.
个解.
更多信息

- 数学函数,适合符号和数值运算.
- 根据解的虚部对解排序.
- 对于
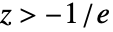 ,ProductLog[z] 是实数.
,ProductLog[z] 是实数. - ProductLog[z] 满足微分方程
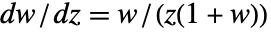 .
. - 对某些特定参数,ProductLog 自动运算出精确值.
- ProductLog 可求任意数值精度的值.
- ProductLog 逐项作用于列表的各个元素. »
- ProductLog[z] 在定义域从
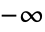 到
到 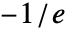 的复平面 z 上有一个分支线.
的复平面 z 上有一个分支线. - ProductLog[k,z] 允许 k 为任意整数,其中
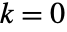 对应于主解.
对应于主解. - 当整数
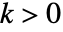 ,ProductLog[k,z] 在
,ProductLog[k,z] 在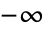 到 0 有一个分支线.
到 0 有一个分支线. - ProductLog 可与 Interval 和 CenteredInterval 对象一起使用. »
范例
打开所有单元关闭所有单元基本范例 (6)
范围 (36)
数值计算 (6)
或用 MatrixFunction 计算矩阵形式的 ProductLog 函数:
ProductLog 可与 Interval 和 CenteredInterval 对象一起使用:
特殊值 (4)
可视化 (3)
函数的属性 (10)
ProductLog 对于所有在区间 [-![]() ,∞) 的实数由定义:
,∞) 的实数由定义:
ProductLog 为所有复数定义:
ProductLog 不是解析函数:
ProductLog 在实定义域上递增:
ProductLog 是单射函数:
ProductLog 不是满射函数:
ProductLog 既不是非负,也不是非正:
ProductLog 在 (-∞,-![]() ] 内有奇点和断点:
] 内有奇点和断点:
ProductLog 在它的实数域上是凹函数:
TraditionalForm 格式:
积分 (3)
级数展开 (5)
函数恒等与简化 (2)
应用 (11)
利用 ProductLog 求解方程:
绘制 ProductLog 的黎曼面:
当一根火柴点燃时,产生的火焰球从半径为 ![]() 开始,迅速增长直到达到一定大小,并保持这种状态,因为火焰球内部燃烧消耗的氧气量与表面的氧气量相平衡. 定义一个模拟火焰传播的函数:
开始,迅速增长直到达到一定大小,并保持这种状态,因为火焰球内部燃烧消耗的氧气量与表面的氧气量相平衡. 定义一个模拟火焰传播的函数:
在 ![]() 范围内可视化简化的火焰传播模型,该模型在
范围内可视化简化的火焰传播模型,该模型在 ![]() 之前显示出适度的增长,然后在短暂的快速增长之后逐渐减弱:
之前显示出适度的增长,然后在短暂的快速增长之后逐渐减弱:
计算 Gram 点:
显示好的 Gram 点,即 RiemannSiegelZ 在连续点上改变符号:
属性和关系 (5)
文本
Wolfram Research (1996),ProductLog,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ProductLog.html (更新于 2022 年).
CMS
Wolfram 语言. 1996. "ProductLog." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2022. https://reference.wolfram.com/language/ref/ProductLog.html.
APA
Wolfram 语言. (1996). ProductLog. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ProductLog.html 年