ProductLog

ProductLog[z]

gives the principal solution for w in .

ProductLog[k,z]

gives the k^(th) solution.

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • The solutions are ordered according to their imaginary parts.
  • For 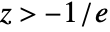, ProductLog[z] is real.
  • ProductLog[z] satisfies the differential equation .
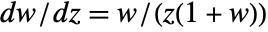  • For certain special arguments, ProductLog automatically evaluates to exact values.
  • ProductLog can be evaluated to arbitrary numerical precision.
  • ProductLog automatically threads over lists. »
  • ProductLog[z] has a branch cut discontinuity in the complex z plane running from 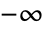to .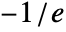
  • ProductLog[k,z] allows k to be any integer, with 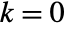corresponding to the principal solution.
  • ProductLog[k,z] for integer 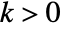has a branch cut discontinuity from 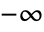to 0.
  • ProductLog can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (6)

Evaluate numerically:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Series expansion at the origin:

Asymptotic expansions at Infinity:

Asymptotic expansions at a singular point:

Scope  (36)

Numerical Evaluation  (6)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number input:

Evaluate efficiently at high precision:

Compute the elementwise values of an array using automatic threading:

Or compute the matrix ProductLog function using MatrixFunction:

ProductLog can be used with Interval and CenteredInterval objects:

Specific Values  (4)

Values of ProductLog at fixed points:

Values at zero:

Values at infinity:

Find a value of x for which the ProductLog[x]=0.5 using FindRoot:

Visualization  (3)

Plot the ProductLog function:

Plot the real part of :

Plot the imaginary part of :

Polar plot with :

Function Properties  (10)

ProductLog is defined for all real values from the interval [-,∞):

ProductLog is defined for all complex values:

The two-argument form requires that be an integer and :

The real range:

ProductLog is not an analytic function:

Nor is it meromorphic:

ProductLog is increasing on its real domain:

ProductLog is injective:

ProductLog is not surjective:

ProductLog is neither non-negative nor non-positive:

ProductLog has both singularity and discontinuity in (-∞,-]:

ProductLog is concave on its real domain:

TraditionalForm formatting:

Differentiation  (3)

The first derivative with respect to z:

Higher derivatives with respect to z:

Plot the higher derivatives with respect to z:

Derivative of a nested logarithmic function:

Integration  (3)

Compute the indefinite integral using Integrate:

Verify the anti-derivative:

Definite integral of ProductLog:

More integrals:

Series Expansions  (5)

Find the Taylor expansions using Series:

Plots of the first three approximations around :

Expand the two-argument form:

The general term in the series expansion using SeriesCoefficient:

Find the series expansion at Infinity:

Find series expansions at branch points and branch cuts:

The series expansion at infinity contains nested logarithms:

Function Identities and Simplifications  (2)

ProductLog gives the solution for the following equation:

Expand assuming real variables x and y:

Generalizations & Extensions  (3)

Evaluate numerically on different sheets of the Riemann surface:

Find series expansions at branch points and branch cuts:

The branch points and branch cuts are different for :

Applications  (11)

Solve an equation in terms of ProductLog:

Plot the real and imaginary parts of ProductLog:

Plot the Riemann surface of ProductLog:

Calculate the limit of :

Compare the exact result with explicit iterations for :

Determine the number of labeled unrooted trees from the generating function:

Solve the Lotka–Volterra equations:

Find the frequency of the maximum of the Planck blackbody spectrum:

Solve the Haissinski equation:

When a match is lit, the resulting ball of flame starts with a radius of , grows rapidly until it reaches a certain size and stays that way, because the amount of oxygen being consumed by the combustion within the ball of flame is balanced by the amount available from the surface. Define a function modeling the flame propagation:

Show that the function satisfies a simple nonlinear differential equation:

Visualize the simplified flame propagation model over the range , which shows modest growth until and then tapers off after a short interval of rapid growth:

Equipotential curves of a plate capacitor:

Compute Gram points:

Show good Gram points, where RiemannSiegelZ changes sign for consecutive points:

Show a bad Gram point:

Properties & Relations  (5)

ProductLog is the inverse function of :

Compositions with the inverse function may need PowerExpand:

Use FullSimplify to simplify expressions containing ProductLog:

Solve a transcendental equation:

Integrals:

Possible Issues  (2)

Generically :

On branch cuts, machine‐precision inputs can give numerically wrong answers:

Use arbitrary‐precision arithmetic to get correct results:

Neat Examples  (2)

Nested derivatives:

Nested integrals:

Wolfram Research (1996), ProductLog, Wolfram Language function, https://reference.wolfram.com/language/ref/ProductLog.html (updated 2022).

Text

Wolfram Research (1996), ProductLog, Wolfram Language function, https://reference.wolfram.com/language/ref/ProductLog.html (updated 2022).

CMS

Wolfram Language. 1996. "ProductLog." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/ProductLog.html.

APA

Wolfram Language. (1996). ProductLog. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ProductLog.html

BibTeX

@misc{reference.wolfram_2025_productlog, author="Wolfram Research", title="{ProductLog}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ProductLog.html}", note=[Accessed: 11-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_productlog, organization={Wolfram Research}, title={ProductLog}, year={2022}, url={https://reference.wolfram.com/language/ref/ProductLog.html}, note=[Accessed: 11-May-2025 ]}