RamanujanTauZ
给出 Ramanujan τ Z 函数 ![]() .
.
更多信息

- 数学函数,适合于符号和数值处理.
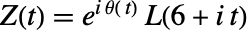 ,其中
,其中 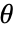 是 Ramanujan τ θ 函数,
是 Ramanujan τ θ 函数,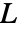 是 Ramanujan τ L 函数.
是 Ramanujan τ L 函数.- 当
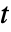 为实数时,
为实数时,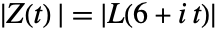 .
. - 除了虚轴上
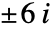 到
到 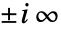 的分支切割外,
的分支切割外,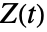 是
是 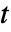 的解析函数.
的解析函数. - 对于某些特定自变量,RamanujanTauZ 自动求解精确值.
- RamanujanTauZ 可以计算到任意数值精度.
- RamanujanTauZ 自动逐项作用于列表.
范例
打开所有单元关闭所有单元范围 (22)
数值计算 (6)
用 Around 计算普通的统计区间:
或用 MatrixFunction 计算矩阵形式的 RamanujanTauZ 函数:
特殊值 (3)
可视化 (2)
函数属性 (9)
所有实数有 RamanujanTauZ 定义:
RamanujanTauZ 的近似函数范围:
RamanujanTauZ 线性作用于列表:
RamanujanTauZ 是 x 的解析函数:
RamanujanTauZ 既不是非递增,也不是非递减:
RamanujanTauZ 不是单射函数:
RamanujanTauZ 既不是非负,也不是非正:
RamanujanTauZ 没有奇点或断点:
RamanujanTauZ 既不凸,也不凹:
级数展开 (2)
应用 (4)
绘制 RamanujanTauZ 的绝对值的图形:
On the critical line, RamanujanTauL splits:
显示 Sin[RamanujanTauTheta[t]] 和 RamanujanTauZ[t]] 的根的交错关系:
属性和关系 (3)
在临界线,RamanujanTauZ 是 RamanujanTauL 的模,最多差一个符号:
RamanujanTauZ 可以用 RamanujanTauL 和 RamanujanTauTheta 来表示:
文本
Wolfram Research (2007),RamanujanTauZ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RamanujanTauZ.html.
CMS
Wolfram 语言. 2007. "RamanujanTauZ." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/RamanujanTauZ.html.
APA
Wolfram 语言. (2007). RamanujanTauZ. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RamanujanTauZ.html 年