Rationalize
Rationalize[x]
converts an approximate number x to a nearby rational with small denominator.
Rationalize[x,dx]
yields the rational number with smallest denominator that lies within dx of x.
Details
- Rationalize[x,dx] works with exact numbers x.
- Rationalize[x] yields x unchanged if there is no rational number close enough to x to satisfy the condition
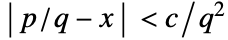 , with
, with 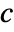 chosen to be
chosen to be 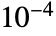 .
. - Rationalize[x,0] converts any inexact number x to rational form. »
Examples
open allclose allScope (5)
Find rational approximations to within a given tolerance:
Rationalize works with exact numbers:
Rationalize all numbers in an expression:
No rational number is by default considered "close enough" to N[Pi]:
Applications (3)
Properties & Relations (3)
If Rationalize returns a rational number ![]() , then
, then ![]() :
:
When Rationalize[x] returns x unchanged, there is no rational number satisfying this:
Get the rational approximations with smallest denominator error dx through machine precision:
The residual of the inequality is positive for all of these rational approximations:
SetPrecision[x,∞] and Rationalize[x,0] both give rational approximations for real x:
Rationalize[x,0] gives a rational that is equivalent to x up to the precision of x:
SetPrecision[x,∞] gets a rational directly from the bitwise representation of x:
Rationalize and RootApproximant both give exact quantities approximating real x:
RootApproximant[x] gives an algebraic number equivalent to x up to the precision of x:
Rationalize[x,0] gives a rational number equivalent to x up to the precision of x:
Text
Wolfram Research (1988), Rationalize, Wolfram Language function, https://reference.wolfram.com/language/ref/Rationalize.html (updated 1999).
CMS
Wolfram Language. 1988. "Rationalize." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1999. https://reference.wolfram.com/language/ref/Rationalize.html.
APA
Wolfram Language. (1988). Rationalize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Rationalize.html