LatticeReduce

LatticeReduce[{v1,v2,…}]

gives a reduced basis for the set of vectors vi.

Details

  • The elements of the vi can be integers, Gaussian integers, or Gaussian rational numbers.

Examples

open allclose all

Basic Examples  (1)

Find the reduced norm basis for a lattice:

Applications  (3)

Starting with trivial integer linear relationships, LatticeReduce can produce more interesting ones:

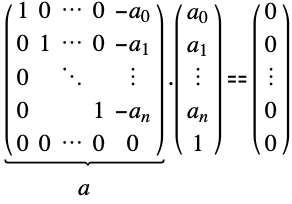
Find integer linear relationships for and of the form :

LatticeReduce preserves linear relationships, and the third row provides , , and :

Find polynomial relationships for :

The trivial initial relationships:

The reduced relationships:

The first relationship:

Find linear relationships x0+x1 ArcTan[1]+x2 ArcTan[1/5]+x3 ArcTan[1/239]==0:

Initial trivial relationships:

Reduced relationships:

The first relationship:

Properties & Relations  (2)

LatticeReduce produces a new reduced basis for the same lattice:

The product of the norms will decrease:

The determinant or volume of the generator cell is preserved:

The lattice is generated by {v1,v2}, but also by {w1,w2} produced by LatticeReduce:

The original cell is pink, and the one produced by LatticeReduce is cyan:

Possible Issues  (1)

The set of vectors must have rational or Gaussian rational coefficients:

Wolfram Research (1988), LatticeReduce, Wolfram Language function, https://reference.wolfram.com/language/ref/LatticeReduce.html.

Text

Wolfram Research (1988), LatticeReduce, Wolfram Language function, https://reference.wolfram.com/language/ref/LatticeReduce.html.

CMS

Wolfram Language. 1988. "LatticeReduce." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LatticeReduce.html.

APA

Wolfram Language. (1988). LatticeReduce. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LatticeReduce.html

BibTeX

@misc{reference.wolfram_2024_latticereduce, author="Wolfram Research", title="{LatticeReduce}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/LatticeReduce.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_latticereduce, organization={Wolfram Research}, title={LatticeReduce}, year={1988}, url={https://reference.wolfram.com/language/ref/LatticeReduce.html}, note=[Accessed: 21-December-2024 ]}