FindIntegerNullVector

FindIntegerNullVector[{x1,x2,…,xn}]

finds a list of integers such that .

FindIntegerNullVector[{x1,x2,…,xn},d]

finds a list of integers with TemplateBox[{{{, {{a, _, 1}, ,, ..., ,, {a, _, n}}, }}}, Norm]<=d such that .

Details and Options

  • FindIntegerNullVector is also known as PSLQ or number identification.
  • Not all ai are zero. The numbers xi can be real or complex. For complex numbers xi the numbers ai are Gaussian integers.
  • In FindIntegerNullVector[{x1,x2,…},d] no integer null vector may exist with the given norm bound. The input is then returned unevaluated.
  • The following options can be given:
  • WorkingPrecision Automaticprecision to use in internal computation
    ZeroTest Automaticmethod to test whether a number is zero
  • The setting ZeroTest->Automatic automatically determines the method to test the integer relation .
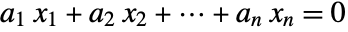  • For inexact numbers xi, the relation found holds up to the precision of the input. For exact numbers xi, the relation found is validated using PossibleZeroQ.
  • For inexact numbers xi and WorkingPrecision->Automatic the precision is taken to be the precision of the input.
  • For exact numbers xi and WorkingPrecision->Automatic the precision is taken to start with MachinePrecision and use up to $MaxExtraPrecision extra precision when searching for an integer null vector when no norm bound d is specified. In the case of a norm bound d, enough precision is used to either find a null vector or prove that none exist.

Examples

open allclose all

Basic Examples  (3)

Exact input:

Inexact input:

Exact input with norm bound:

There is no null vector with norm less than or equal to 2:

Scope  (6)

This finds an integer null vector for a vector of exact real numbers:

This proves that there is no null vector with norm less than or equal to 8:

For a bound close to the norm of a null vector you may not get proof that no null vector exists:

The returned null vector does not satisfy the norm bound:

FindIntegerNullVector cannot prove that numbers are linearly independent over the integers:

It can prove that there is no integer null vector with norm less than or equal to a given bound:

For inexact input, the relation is true up to the precision of the input:

No null vector exists for the given norm bound:

Here no null vector is found, but nonexistence of a null vector is proven only for a smaller norm bound:

This finds a null vector for a 20-digit approximation of :

The result is not a null vector for the exact vector :

A null vector found for a higher-precision approximation of is also a null vector for :

This gives a Gaussian integer null vector for a vector of exact complex numbers:

This finds a Gaussian integer null vector for a vector of approximate complex numbers:

Options  (2)

WorkingPrecision  (1)

By default, precision of at most $MachinePrecision+$MaxExtraPrecision digits is used:

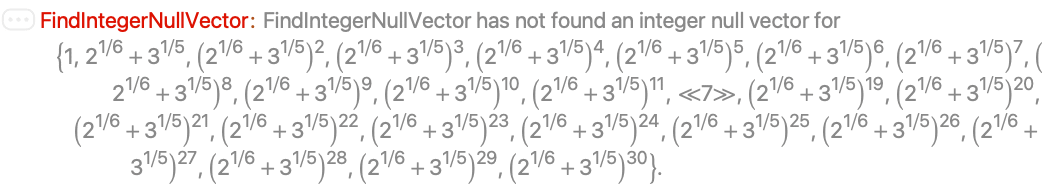
Using a higher WorkingPrecision allows you to find a null vector:

ZeroTest  (1)

By default, PossibleZeroQ with Method->"ExactAlgebraics" is used to prove relations:

This uses exact methods to prove the relation:

This uses a high-precision numeric test instead:

Applications  (3)

Find coefficients of the minimal polynomial of an algebraic number:

This finds the minimal polynomial using symbolic methods:

Find a relation between transcendental numbers:

Find the coefficients in Machin's formula for computing approximations of :

Properties & Relations  (3)

FindIntegerNullVector returns an integer null vector for the given vector:

An integer null vector is a nontrivial integer solution of a homogeneous linear equation:

Use FindInstance to find solutions of equations:

Find coefficients of the minimal polynomial of an algebraic number using its approximation:

Use RootApproximant to find an algebraic number using its approximation:

Possible Issues  (2)

The precision of an approximation may not be sufficient to find a relation between numbers:

Using a higher-precision approximation, you get a true relation:

Numeric zero testing used for nonalgebraic numbers may allow results that are not null vectors:

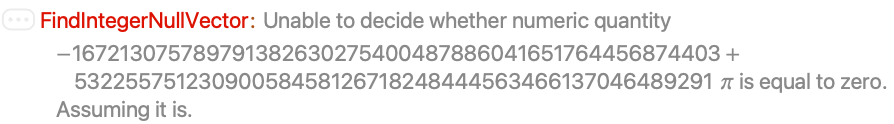
This gives the precision used in zero testing when no symbolic zero-testing method applies:

With a higher zero-testing precision, FindIntegerNullVector correctly rejects the vector:

Reset the system option to the original value:

Wolfram Research (2010), FindIntegerNullVector, Wolfram Language function, https://reference.wolfram.com/language/ref/FindIntegerNullVector.html.

Text

Wolfram Research (2010), FindIntegerNullVector, Wolfram Language function, https://reference.wolfram.com/language/ref/FindIntegerNullVector.html.

CMS

Wolfram Language. 2010. "FindIntegerNullVector." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FindIntegerNullVector.html.

APA

Wolfram Language. (2010). FindIntegerNullVector. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindIntegerNullVector.html

BibTeX

@misc{reference.wolfram_2024_findintegernullvector, author="Wolfram Research", title="{FindIntegerNullVector}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/FindIntegerNullVector.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findintegernullvector, organization={Wolfram Research}, title={FindIntegerNullVector}, year={2010}, url={https://reference.wolfram.com/language/ref/FindIntegerNullVector.html}, note=[Accessed: 21-November-2024 ]}