Rationalize

Rationalize[x]

选取 x 的有理近似值，并把它们转换成有理数.

Rationalize[x,dx]

当 x 的误差小于 dx 时，转换为具有最小分母的有理数.

更多信息

  • Rationalize[x,dx] 对精确数 x 起作用.
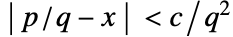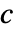  • 如果没有有理数足够接近 x 并满足条件 （其中 为 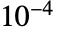），Rationalize[x] 产生的 x 保持不变.
  • Rationalize[x,0] 把任何不精确数 x 转换成有理格式. »

范例

打开所有单元关闭所有单元

基本范例  (1)

转化为一个有理数：

范围  (5)

在给定的公差下求有理近似值：

Rationalize 对于精确数起作用：

在一个表达式中，将所有数转换为有理数：

缺省下没有有理数被认为足够接近 N[Pi]：

指定一个有理近似值：

应用  (3)

的连续有理近似值：

与 的有理近似值比较，逐步绘制误差会更合理：

与 的有理近似值比较，逐步绘制误差会更合理：

创建一个有近似数值系数的多项式：

求关于有理数的一个近似值：

提取因子：

属性和关系  (3)

如果 Rationalize 返回一个有理数 ，则 ：

当 Rationalize[x] 返回 x 的不变化的形式，表示没有有理数满足条件：

获得有理近似值，其最小公分母的误差 dx 在机器精度内：

不等式的余式对所有这些有理近似值是正的：

SetPrecision[x,∞] 和 Rationalize[x,0] 同时给出关于实数 x 的有理近似值：

Rationalize[x,0] 给出等价于 x 的有理数，其精度取决于 x：

SetPrecision[x,∞] 从 x 的按位表示中直接获得有理数：

Rationalize 和 RootApproximant 给出近似于实数 x 的明确数：

RootApproximant[x] 给出等价于 x 的代数数，其精度取决于 x：

Rationalize[x,0] 给出等价于 x 的有理数，其精度取决于 x：

Wolfram Research (1988)，Rationalize，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Rationalize.html （更新于 1999 年）.

文本

Wolfram Research (1988)，Rationalize，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Rationalize.html （更新于 1999 年）.

CMS

Wolfram 语言. 1988. "Rationalize." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 1999. https://reference.wolfram.com/language/ref/Rationalize.html.

APA

Wolfram 语言. (1988). Rationalize. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Rationalize.html 年

BibTeX

@misc{reference.wolfram_2024_rationalize, author="Wolfram Research", title="{Rationalize}", year="1999", howpublished="\url{https://reference.wolfram.com/language/ref/Rationalize.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rationalize, organization={Wolfram Research}, title={Rationalize}, year={1999}, url={https://reference.wolfram.com/language/ref/Rationalize.html}, note=[Accessed: 21-November-2024 ]}