RollPitchYawAngles

RollPitchYawAngles[r]

gives the roll-pitch-yaw angles {α,β,γ} corresponding to the rotation matrix r.

RollPitchYawAngles[r,{a,b,c}]

gives the roll-pitch-yaw angles {α,β,γ} corresponding to rotation order {a,b,c}.

Details

  • RollPitchYawAngles is used to decompose into fixed axis-oriented rotations.
  • RollPitchYawAngles[r,{a,b,c}] gives angles {α,β,γ} such that RollPitchYawMatrix[{α,β,γ},{a,b,c}]r.
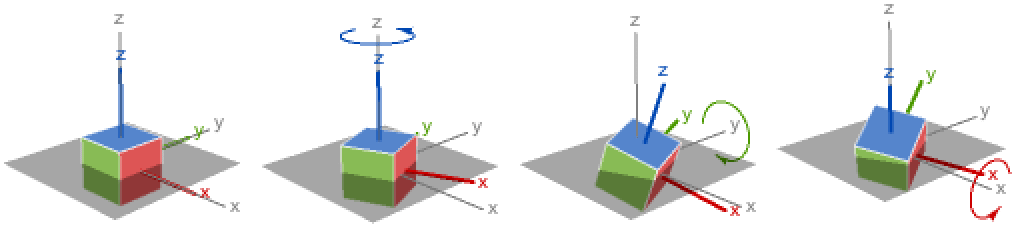
  • RollPitchYawAngles[r] is equivalent to RollPitchYawAngles[r,{3,2,1}], the z-y-x rotation.
  • The default z-y-x angles RollPitchYawAngles[r,{3,2,1}] decompose rotation into three steps:
  • The rotation axes a, b, and c can be any integer 1, 2, or 3, but there are only twelve combinations that are general enough to be able to specify any 3D rotation.
  • Rotations with the first and last axis repeated:
  • {3,2,3}z-y-z rotation
    {3,1,3}z-x-z rotation
    {2,3,2}y-z-y rotation
    {2,1,2}y-x-y rotation
    {1,3,1}x-z-x rotation
    {1,2,1}x-y-x rotation
  • Rotations with all three axes different:
  • {1,2,3}x-y-z rotation
    {1,3,2}x-z-y rotation
    {2,1,3}y-x-z rotation
    {2,3,1}y-z-x rotation
    {3,1,2}z-x-y rotation
    {3,2,1}z-y-x rotation (default)
  • Rotations with subsequent axes repeated may not be invertible since these are not capable of representing all possible rotations in 3D.

Examples

open allclose all

Basic Examples  (2)

Get roll-pitch-yaw angles from the rotation matrix:

Get roll-pitch-yaw angles from the rotation matrix with the given rotation order:

Scope  (2)

Get roll-pitch-yaw angles from a rotation matrix:

Get roll-pitch-yaw angles from a rotation matrix with the given rotation order:

Properties & Relations  (1)

RollPitchYawAngles returns angles for which RollPitchYawMatrix gives the same rotation matrix:

The angles need not be the same:

However, both sets of angles produce the same rotation matrix:

Possible Issues  (1)

RollPitchYawMatrix allows equal consecutive axes, and this generates a rotation matrix:

However, RollPitchYawAngles requires consecutive axes to be distinct:

This is because with consecutive axes equal, some rotation matrices cannot be represented:

Wolfram Research (2015), RollPitchYawAngles, Wolfram Language function, https://reference.wolfram.com/language/ref/RollPitchYawAngles.html.

Text

Wolfram Research (2015), RollPitchYawAngles, Wolfram Language function, https://reference.wolfram.com/language/ref/RollPitchYawAngles.html.

CMS

Wolfram Language. 2015. "RollPitchYawAngles." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RollPitchYawAngles.html.

APA

Wolfram Language. (2015). RollPitchYawAngles. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RollPitchYawAngles.html

BibTeX

@misc{reference.wolfram_2024_rollpitchyawangles, author="Wolfram Research", title="{RollPitchYawAngles}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/RollPitchYawAngles.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rollpitchyawangles, organization={Wolfram Research}, title={RollPitchYawAngles}, year={2015}, url={https://reference.wolfram.com/language/ref/RollPitchYawAngles.html}, note=[Accessed: 21-November-2024 ]}