WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

SourcePDETerm

SourcePDETerm[vars,f]

ソース係数，モデル変数 vars のソース項を表す．

SourcePDETerm[vars,f,pars]

モデルパラメータ pars を使う．

詳細

ソース項は，熱力学，音響学，物理学，流体力学のような数多くの分野で使用される．
ソースは，一般に，ソースあるいはシンクのモデル化に使われる．
ソース係数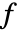にソースを加えることは，以下でモデルにエネルギーを加えたりモデルからエネルギーを除去したりする過程である．

SourcePDETermは，偏微分方程式の一部として使われる微分演算子項を返す．

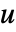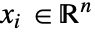SourcePDETermを使って，方程式中のソースが，従属変数，独立変数，時間変数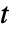でモデル化できる．
定常モデル変数 vars は vars={u[x₁,…,x_n],{x₁,…,x_n}}である．
時間依存モデル変数 vars は vars={u[t,x₁,…,x_n],{x₁,…,x_n}}または vars={u[t,x₁,…,x_n],t,{x₁,…,x_n}}である．
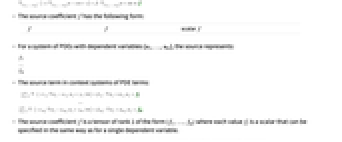
他のPDE項との関連におけるソース項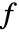は以下で与えられる．

ソース係数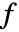は次の形式である．
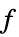
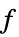
スカラー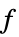
従属変数{u₁,…,u_m}がある偏微分方程式系については，ソースは以下を表す．

次は，PDE項の系の関連におけるソース項である．

ソース係数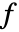は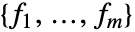の形をした階数1のテンソルである．各値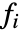は単独の従属変数と同じように指定できるスカラーである．
ソース係数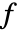は，時間，空間，パラメータ，従属変数に依存することがある．
係数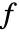はNeumannValueの意味に影響しない．
与えられた独立変数に明示的に依存しない数量はすべて，ゼロ偏微分を持つものとみなされる．

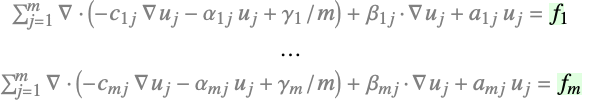
例題

すべて開くすべて閉じる

例 (3)

時間非依存のソース項を定義する：

時間依存のソース項を定義する：

拡散項とソース項で構築されたポアソン方程式を解く：

スコープ (6)

記号的なソース項を定義する：

2Dの定常ソース項を定義する：

複数の従属変数についてのソース項を定義する：

ソース項があるポアソン(Poisson)方程式を解く：

拡散項とソース項から構築されたポアソン方程式の固有値を計算する：

ヘルムホルツ(Helmholtz)モデルを定義する：

ソース項があるヘルムホルツ方程式を解く：

解を可視化する：

トップへ