StateResponse

StateResponse[sys,u,{t,tmin,tmax}]

入力 u に対する状態空間モデル sys の数値状態応答を tmin≤t≤tmaxについて与える．

StateResponse[sys,{u[0],u[1],…}]

入力数列 u[i]に対する離散時間状態空間モデル ssm の応答を与える．

StateResponse[sys,u,t]

記号状態応答を時間 t の関数として与える．

StateResponse[sys,{u1,…,um},…]

複数の入力 uiへの状態応答を与える．

StateResponse[{sys,{x10,x20,…,xn0}},…, …]

初期条件 xi0の応答を与える．

詳細

  • StateResponseは，与えられた入力 u について状態微分方程式あるいは状態差分方程式を解く．
  • 状態空間モデル sys は，StateSpaceModel，連続時間AffineStateSpaceModelあるいは連続時間NonlinearStateSpaceModelである．
  • 線形StateSpaceModel sys もまた，ディスクリプタで遅延系であり得る．
  • 初期状態 xi0は，他に指定がない限り，sys の状態操作値であるとみなされる．
  • ディスクリプタ系については，初期状態が矛盾してはならない．
  • 遅延系については，初期状態は履歴を含み，t≤0について xi0[t]として与えることができる． »

例題

すべて開くすべて閉じる

例  (4)

単位ステップ入力に対する連続時間系の状態応答：

初期条件が{1,-1}の離散時間系の応答：

ディラックデルタ入力に対する系の状態応答：

時間遅延系のステップ応答：

スコープ  (26)

連続時間系  (16)

単位ステップに対する単一入力系の状態応答：

初期条件は0であるとみなされる：

一般的な連続時間系の状態応答：

単位ステップ入力に対する応答：

ディスクリプタStateSpaceModelの応答：

代数方程式で：

正弦波入力に対する数値応答：

{0.2,0.1}を初期状態値として指定する：

二入力系の入力信号{SquareWave[t],Sin[t]}に対する応答：

入力{Sin[t],Cos[t],Cos[t]}に対する三入力系の状態応答：

応答をプロットする：

入力信号数が系の入力数より少ない場合，残りの入力は0であるとみなされる：

多入力系についてスカラー入力信号が指定された場合，信号は各入力に対して順番に適用される：

StateResponse[…,{t,tmin,tmax}]は結果を補間関数オブジェクトで与える：

応答をプロットする：

特異ディスクリプタ系のステップ応答：

特異ディスクリプタ系への記号応答：

応答をプロットする：

UnitStep入力へのAffineStateSpaceModelの状態応答：

応答をプロットする：

非零の初期条件からの応答：

NonlinearStateSpaceModelの正弦波入力への状態応答：

応答をプロットする：

離散時間系  (10)

単一入力系の単位ステップ入力への状態応答：

応答を8ステップ分プロットする：

一般的な離散時間系の応答：

単位ステップ列に対する応答：

記号ディスクリプタ系への応答：

サンプルの正弦曲線に対する状態応答：

ゼロ次ホールドで応答をプロットする：

2つのランダムにサンプル入力に対する二入力系の状態応答：

ランダムな入力数列に対する応答：

二入力状態空間モデル：

1つの入力信号だけが与えられると，残りの入力は0に設定される：

2番目と4番目の状態は2番目の入力が0であるために励起されていない：

多入力系に単一入力列が与えられた場合，これは各入力に順番に適用される：

離散時間時間遅延系は k0までの時間ステップの履歴を受容する：

一般化と拡張  (3)

初期時間は，指定されていない場合は0であるとみなされる：

状態遅延系の初期状態は履歴を含むことができる：

遅延をともなう離散時間系では，初期状態は数列で与えることができる：

アプリケーション  (4)

動いている台車の上の安定した倒立振子のモデルは，振子の角位置 θ と速度 ω および台車の変位 d と速度 v を状態変数として持つ：

StateResponseを使って得られた台車の速度と振子の角速度を微分して台車の加速 a と振子の角加速 α を計算する：

結果をプロットする：

多入力系の各制御入力に対する状態の応答を分析する：

所望の生産速度と販売速度を入力とし実際の生産速度と在庫レベルを状態とした，生産と在庫の管理システムの状態空間モデル：

与えられた生産速度についての応答と最初の均衡条件から10%販売がアップする応答を求める：

特定の初期条件についての応答をプロットする：

Clohessy–Wiltshire方程式は中心体の軌道を回る2つの衛星間の相対運動をモデル化する：

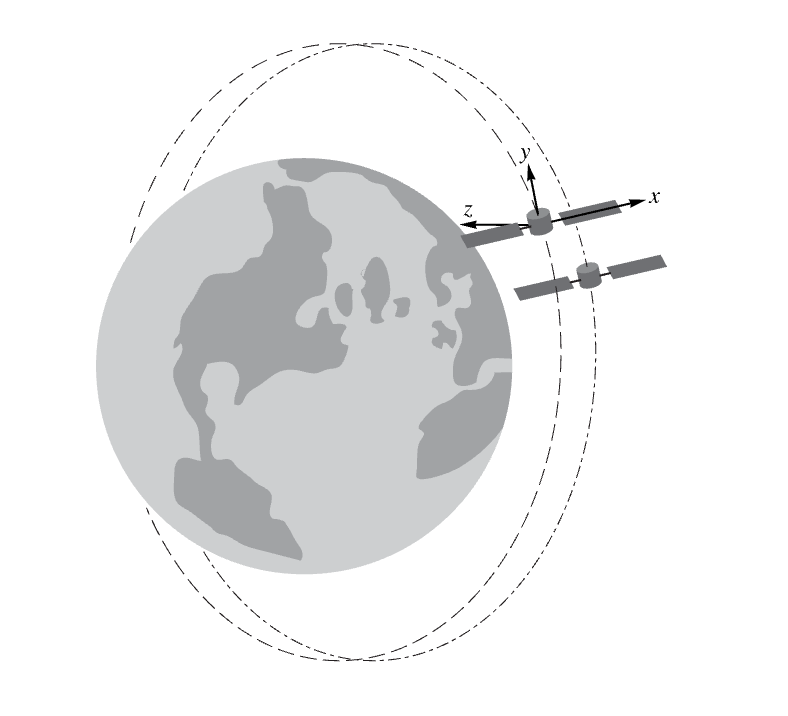
StateResponseを使って特定の打ち上げ条件群から閉じた相対軌道を得る：

特性と関係  (3)

StateResponseとOutputResponseの結果は状態出力については等しい：

出力行列が恒等行列で伝送行列が0の場合に状態出力が起る：

自然応答は系の極によって決定される：

これは同じようなどの変換でも変わらない：

最初の状態：

ディスクリプタ系の初期状態は入力と矛盾がないように選ばれる：

第2状態は入力の導関数に等しい：

矛盾する条件が与えられると，それらは置き換えられる：

KroneckerModelDecompositionにおける遅い部分系に依存する矛盾しない初期状態：

連続時間系では，初期条件は で与えられる：

考えられる問題  (2)

記号状態応答は時間遅延をサポートしない：

数値によるシミュレーションを試みる：

ディスクリプタ系では，解は何らかの λ についてDet[λ e - a]≠0のときにのみ存在する：

Wolfram Research (2010), StateResponse, Wolfram言語関数， https://reference.wolfram.com/language/ref/StateResponse.html （2014年に更新）.

テキスト

Wolfram Research (2010), StateResponse, Wolfram言語関数， https://reference.wolfram.com/language/ref/StateResponse.html （2014年に更新）.

CMS

Wolfram Language. 2010. "StateResponse." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/StateResponse.html.

APA

Wolfram Language. (2010). StateResponse. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StateResponse.html

BibTeX

@misc{reference.wolfram_2024_stateresponse, author="Wolfram Research", title="{StateResponse}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/StateResponse.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_stateresponse, organization={Wolfram Research}, title={StateResponse}, year={2014}, url={https://reference.wolfram.com/language/ref/StateResponse.html}, note=[Accessed: 17-November-2024 ]}