StateResponse
StateResponse[sys,u,{t,tmin,tmax}]
gives the numeric state response of the state-space model sys to input u for tmin≤t≤tmax.
StateResponse[sys,{u[0],u[1],…}]
gives the response of the discrete-time state-space model sys to the input sequence u[i].
StateResponse[sys,u,t]
gives the symbolic state response as a function of time t.
StateResponse[sys,{u1,…,um},…]
gives the state response for multiple inputs ui.
StateResponse[{sys,{x10,x20,…,xn0}},…, …]
gives the response with initial states xi0.
Details
- StateResponse solves the state differential or difference equations for the given input u.
- The state-space model sys can be a StateSpaceModel, a continuous-time AffineStateSpaceModel, or a continuous-time NonlinearStateSpaceModel.
- A linear StateSpaceModel sys can also be a descriptor and delay system.
- The initial states xi0 are taken to be the state operating values of sys unless specified.
- For descriptor systems, the initial states need to be consistent.
- For delay systems, the initial states include history and can be given as xi0[t] for t≤0. »
Examples
open allclose allBasic Examples (4)
Scope (26)
Continuous-Time Systems (16)
The state response of a single-input system to a unit step:
The initial conditions are assumed to be zero:
The state response for a generic continuous-time system:
The response to a unit step input:
The response of a descriptor StateSpaceModel:
The numeric response to a sinusoidal input:
Specify {0.2,0.1} as the initial state values:
The response of a two-input system to input signals {SquareWave[t],Sin[t]}:
The state response of a three-input system to inputs {Sin[t],Cos[t],Cos[t]}:
If there are fewer input signals than inputs, the remaining inputs are assumed to be zero:
If a scalar input signal is given for a multiple-input system, it is applied to each input in turn:
StateResponse[…,{t,tmin,tmax}] gives the result in terms of interpolating function objects:
The step response of a singular descriptor system:
The symbolic response for a singular descriptor system:
The state response of an AffineStateSpaceModel to a UnitStep input:
The response from nonzero initial conditions:
The state response of a NonlinearStateSpaceModel to a sinusoidal input:
Discrete-Time Systems (10)
The state response of a single-input system to a unit step input:
Plot the response for eight steps:
The response for a generic discrete-time system:
The response to a unit step sequence:
The response for a symbolic descriptor system:
The state response to a sampled sinusoid:
Plot the response with a zero-order hold:
The state response of a two-input system to two randomly sampled inputs:
The response to a random input sequence:
A two-input state-space model:
When only one input signal is given, the remaining inputs are set to zero:
The second and fourth states are not excited because the second input is zero:
If a single-input sequence is given to a multi-input system, it is applied to each input in turn:
Discrete-time time-delay systems accept a history for time steps before k0:
Generalizations & Extensions (3)
Applications (4)
The model of a stabilized inverted pendulum on a moving cart has the cart displacement d and velocity v, together with the pendulum's angular position θ and velocity ω as the state variables:
Compute the acceleration a of the cart and the angular acceleration α of the pendulum by differentiating the cart's velocity and the pendulum's angular velocity obtained using StateResponse:
Analyze the response of the states to each control input for a multi-input system:
The state-space model of a production and inventory control system with desired production rate and sales rate as inputs and actual production rate and inventory level as states:
Determine the response for a given production rate and 10% jump in sales from the initial equilibrium condition:
Plot the response for specific initial conditions:
The Clohessy–Wiltshire equations model the relative motion between two satellites orbiting a central body:
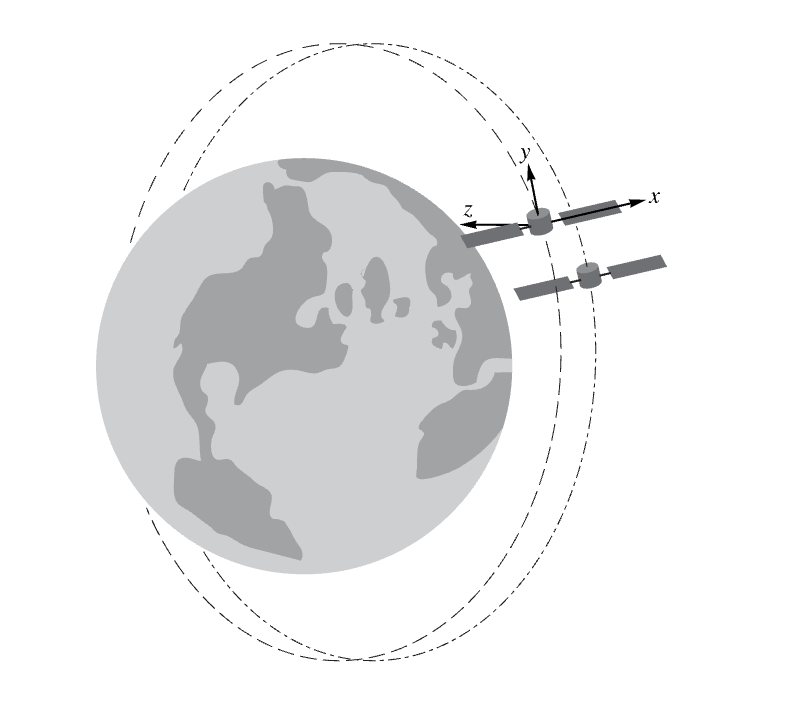
Use StateResponse to obtain the closed relative orbits from a particular set of launch conditions:
Properties & Relations (3)
The results of StateResponse and OutputResponse match for state output:
State output occurs when the output matrix is identity and the transmission matrix is zero:
The natural response is determined by the poles of the system:
It is invariant under any similarity transformation:
The initial states for a descriptor system are chosen to be consistent for the inputs:
The second state equals the derivative of the input:
When inconsistent conditions are given, they are replaced:
Consistent initial states depend on the slow subsystem in KroneckerModelDecomposition:
For continuous-time systems, the initial conditions are given by 
:
Possible Issues (2)
Symbolic state responses do not support time delays:
For descriptor systems, solutions only exist when Det[λ e - a]≠0 for some λ:
Text
Wolfram Research (2010), StateResponse, Wolfram Language function, https://reference.wolfram.com/language/ref/StateResponse.html (updated 2014).
CMS
Wolfram Language. 2010. "StateResponse." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/StateResponse.html.
APA
Wolfram Language. (2010). StateResponse. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StateResponse.html