StateResponse[sys,u,{t,tmin,tmax}]
给出状态-空间模型 sys 对于输入 u 在 tmin≤t≤tmax 时间段内的数字状态响应.
StateResponse[sys,{u[0],u[1],…}]
给出离散时间状态-空间模型 sys 对输入序列 u[i] 的响应.
StateResponse[sys,u,t]
给出作为时间 t 的函数的符号状态响应.
StateResponse[sys,{u1,…,um},…]
给出对多个输入 ui 的状态响应.
StateResponse[{sys,{x10,x20,…,xn0}},…, …]
初始状态为 xi0,给出响应.


StateResponse
StateResponse[sys,u,{t,tmin,tmax}]
给出状态-空间模型 sys 对于输入 u 在 tmin≤t≤tmax 时间段内的数字状态响应.
StateResponse[sys,{u[0],u[1],…}]
给出离散时间状态-空间模型 sys 对输入序列 u[i] 的响应.
StateResponse[sys,u,t]
给出作为时间 t 的函数的符号状态响应.
StateResponse[sys,{u1,…,um},…]
给出对多个输入 ui 的状态响应.
StateResponse[{sys,{x10,x20,…,xn0}},…, …]
初始状态为 xi0,给出响应.
更多信息
- StateResponse 对给定输入 u,求解微分或差分方程.
- 状态-空间模型 sys 可以是 StateSpaceModel、连续时间 AffineStateSpaceModel、或连续时间 NonlinearStateSpaceModel.
- 线性 StateSpaceModel sys 还可以是描述器或延迟系统.
- 除非另行指定,初始值 xi0 被认为是 sys 的状态工作值.
- 描述器系统的初始状态应该是恒定的.
- 延迟系统的初始状态包含历史状态,当 t≤0 时,可以给定为 xi0[t].
范例
打开所有单元 关闭所有单元范围 (25)
连续时间系统 (15)
描述器 StateSpaceModel 的响应:
对输入信号 {SquareWave[t],Sin[t]},双输入系统的响应:
输入为 {Sin[t],Cos[t],Cos[t]} 的三输入系统的状态响应:
如果对多输入系统给出一个标量输入信号,它依次应用于每个输入:
StateResponse[…,{t,tmin,tmax}] 以插值函数对象的结果给出:
AffineStateSpaceModel 对 UnitStep 输入的状态响应:
NonlinearStateSpaceModel 对正弦输入的状态响应:
应用 (4)
在移动车上的稳定倒立摆的模型具有车位移 d 和速度 v,摆的角度位置 θ 和速度 ω 作为稳定变量:
通过微分由 StateResponse 获得的车的速度和摆的角速度,计算车的加速度 a 和摆的角加速度 α:
一个产品和库存控制系统的状态-空间模型,其中所需的产品率和销售率作为输入,实际上的产品率和库存率作为状态:
The Clohessy–Wiltshire equations model the relative motion between two satellites orbiting a central body:
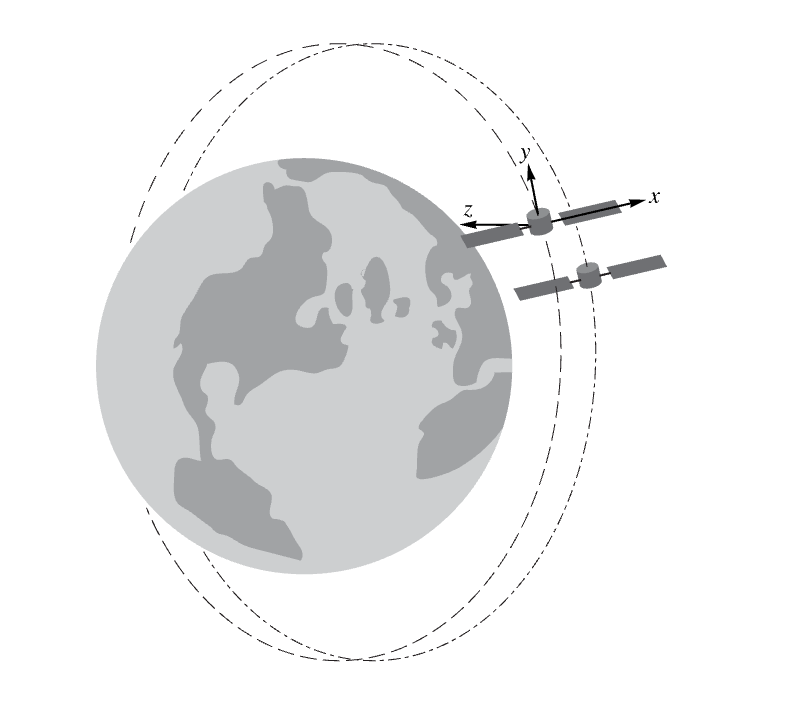
Use StateResponse to obtain the closed relative orbits from a particular set of launch conditions:
属性和关系 (2)
StateResponse 和 OutputResponse 的结果与状态输出匹配:
可能存在的问题 (2)
文本
Wolfram Research (2010),StateResponse,Wolfram 语言函数,https://reference.wolfram.com/language/ref/StateResponse.html (更新于 2014 年).
CMS
Wolfram 语言. 2010. "StateResponse." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/StateResponse.html.
APA
Wolfram 语言. (2010). StateResponse. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/StateResponse.html 年
BibTeX
@misc{reference.wolfram_2025_stateresponse, author="Wolfram Research", title="{StateResponse}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/StateResponse.html}", note=[Accessed: 12-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_stateresponse, organization={Wolfram Research}, title={StateResponse}, year={2014}, url={https://reference.wolfram.com/language/ref/StateResponse.html}, note=[Accessed: 12-March-2026]}