StirlingS1

StirlingS1[n,m]

给出第一类 TemplateBox[{n, m}, StirlingS1] 的 Stirling 数.

更多信息

  • 整数型数学函数，同时适合符号和数值运算.
  • StirlingS1 定义为从离散微积分的 FactorialPower 到连续微积分 TemplateBox[{x, m}, FactorialPower]=sum_(m=1)^n TemplateBox[{n, m}, StirlingS1]x^m 的 Power 的转换矩阵，其中 m,n in TemplateBox[{}, PositiveIntegers].
  • (-1)^(n-m)TemplateBox[{n, m}, StirlingS1] 给出恰好包含 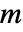个循环的 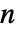个元素置换的个数. »
  • StirlingS1 自动线性作用于列表.

范例

打开所有单元关闭所有单元

基本范例  (1)

计算第一类斯特灵数：

计算多个斯特灵数：

范围  (2)

StirlingS1 按元素线性作用于列表：

TraditionalForm 格式：

应用  (5)

绘制对数尺度下第一类的 Stirling 数：

模 2 斯特灵数：

生成 n 个元素的所有排列的不相交循环表示：

计算具有 1、2、… n 个不相交循环的排列的数量：

第一类无符号斯特林数可计算不相交循环的数量：

绘制对称的组元素中循环的平均数：

在无限序列中的、独立的、恒等分布的连续随机变量的第 个记录的位置的分布：

可视化第二个记录的概率质量函数：

编码来找出给定向量中的第 个位置，如果有：

计算随机指数序列中的第二个记录的位置并将它们的直方图与期望的概率值两函数：

属性和关系  (5)

从普通生成函数生成值：

从指数生成函数生成值：

第一类的 Stirling 数是第二类 Stirling 数的逆：

用柯西定理计算第一类最大的 Stirling 数：

第一类的斯特灵数（ Stirling numbers）由有正负号变化的阶乘自变量的半贝尔多项式给出：

可能存在的问题  (2)

StirlingS1 对适度大小的参数可以有较大的值：

在 的值定义为 1：

巧妙范例  (2)

绘制数字和：

含有斯特林数项的矩阵的行列式：

与解析形式相比较：

Wolfram Research (1988)，StirlingS1，Wolfram 语言函数，https://reference.wolfram.com/language/ref/StirlingS1.html.

文本

Wolfram Research (1988)，StirlingS1，Wolfram 语言函数，https://reference.wolfram.com/language/ref/StirlingS1.html.

CMS

Wolfram 语言. 1988. "StirlingS1." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/StirlingS1.html.

APA

Wolfram 语言. (1988). StirlingS1. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/StirlingS1.html 年

BibTeX

@misc{reference.wolfram_2024_stirlings1, author="Wolfram Research", title="{StirlingS1}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/StirlingS1.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_stirlings1, organization={Wolfram Research}, title={StirlingS1}, year={1988}, url={https://reference.wolfram.com/language/ref/StirlingS1.html}, note=[Accessed: 21-December-2024 ]}