SystemModelSimulateSensitivity[model,{p1,p2,…}]
仿真 model 及其在实验条件设置下对参数 pi 的敏感度.
SystemModelSimulateSensitivity[model,tmax,{p1,p2,…}]
从 0 到 tmax 进行仿真.
SystemModelSimulateSensitivity[model,{tmin,tmax},{p1,p2,…}]
从 tmin 到 tmax 进行仿真.
SystemModelSimulateSensitivity[model,vars,{tmin,tmax},{p1,p2,…}]
只保存变量 vars 的仿真数据.


SystemModelSimulateSensitivity
SystemModelSimulateSensitivity[model,{p1,p2,…}]
仿真 model 及其在实验条件设置下对参数 pi 的敏感度.
SystemModelSimulateSensitivity[model,tmax,{p1,p2,…}]
从 0 到 tmax 进行仿真.
SystemModelSimulateSensitivity[model,{tmin,tmax},{p1,p2,…}]
从 tmin 到 tmax 进行仿真.
SystemModelSimulateSensitivity[model,vars,{tmin,tmax},{p1,p2,…}]
只保存变量 vars 的仿真数据.
更多信息和选项



- 在对系统模型中的参数值进行修改时,可用 SystemModelSimulateSensitivity 来估计仿真结果的变化.
- model 可采用以下形式:
-
SystemModel[…] 通用系统模型 StateSpaceModel[…] 状态空间模型 TransferFunctionModel[…] 传递函数模型 AffineStateSpaceModel[…] 仿射状态空间模型 NonlinearStateSpaceModel[…] 非线性状态空间模型l DiscreteInputOutputModel[…] 离散输入-输出模型l - SystemModelSimulateSensitivity 返回一个 SystemModelSimulationData 对象.
- 对于 SystemModel model,SystemModelSimulateSensitivity 针对所有变量
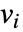 生成解
生成解 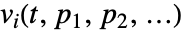 ,为所有状态
,为所有状态 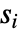 生成导数
生成导数 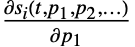 、
、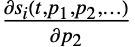 、…,其中
、…,其中 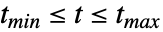 .
. - 对于其他类型的模型,SystemModelSimulateSensitivity 针对所有变量
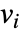 生成解
生成解 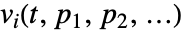 和导数
和导数 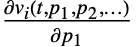 、
、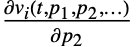 、…,其中
、…,其中 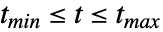 .
. - 可通过 sd["SensitivityNames"] 在 SystemModelSimulationData 对象 sd 中列出敏感度.
- 保存的仿真变量 vars 可以取下列值:
-
Automatic 自动选择要保存的变量 {v1,v2,…} 只保存变量 vi All 保存所有变量 - SystemModelSimulateSensitivity[…,spec] 用 Association spec 来指定初值、参数和输入:
-
"ParameterValues" {p1val1,…} 参数 pi 取值 vali "InitialValues" {v1val1,…} 变量 vi 取初值 vali "Inputs" {in1fun1,…} 输入 ini 在时间点 t 取值 funi[t] - 将 "ParameterValues" 或 "InitialValues" 设为 {pi->{c1,c2,…},…} 以并行方式运行仿真,pi 取值 cj.
- "InitialValues" 对应于 Modelica 模型中的 start 属性.
- 可以给出以下选项:
-
InterpolationOrder Automatic 事件之间的输出的连续性程度 Method Automatic 使用何种仿真方法 ProgressReporting $ProgressReporting 控制进度显示 - 选项设置 Automatic 通常表示设置是从 model 中获取的或为实验设置.
- 对于 SystemModel model,可用 Method->{"opt1"->val1} 控制使用何种 CVODES 求解器 .
- CVODES 方法可能的子选项包括:
-
"InterpolationPoints" Automatic 插值点的数目 "Tolerance" 10-6 自适应步长的容差
范例
打开所有单元 关闭所有单元基本范例 (3)
范围 (16)
模型 (3)
仿真 NonlinearStateSpaceModel 时对变量和敏感度进行计算:
计算 AffineStateSpaceModel 参数扫描的敏感度:
计算 DiscreteInputOutputModel 的敏感度:
选项 (3)
Method (1)
仿真一个 SystemModel,使用模型设置的插值点数量计算灵敏度:
ProgressReporting (1)
用 ProgressReporting 控制进度报告:
应用 (5)
10% 敏感度范围显示 "integrator3.y" 对频率参数最敏感:
用 SystemModelSimulateSensitivity 获取梯度:
属性和关系 (4)
使用 SystemModelPlot:
在图中进行比较,10% 的变化给出的轨迹位于计算所得界限范围之外:
将 SystemModelParametricSimulate 应用于一个可对不同的值进行计算的函数:
文本
Wolfram Research (2018),SystemModelSimulateSensitivity,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SystemModelSimulateSensitivity.html.
CMS
Wolfram 语言. 2018. "SystemModelSimulateSensitivity." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SystemModelSimulateSensitivity.html.
APA
Wolfram 语言. (2018). SystemModelSimulateSensitivity. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SystemModelSimulateSensitivity.html 年
BibTeX
@misc{reference.wolfram_2025_systemmodelsimulatesensitivity, author="Wolfram Research", title="{SystemModelSimulateSensitivity}", year="2018", howpublished="\url{https://reference.wolfram.com/language/ref/SystemModelSimulateSensitivity.html}", note=[Accessed: 10-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_systemmodelsimulatesensitivity, organization={Wolfram Research}, title={SystemModelSimulateSensitivity}, year={2018}, url={https://reference.wolfram.com/language/ref/SystemModelSimulateSensitivity.html}, note=[Accessed: 10-February-2026]}