Threshold
詳細


- 閾値処理は,特定の領域の値をゼロに設定し場合によっては領域外の値を減少させる数学的分割操作である.
- Thresholdは,任意階数のデータ配列や2Dおよび3Dの画像に使うことができる.
- Threshold[data]はThreshold[data,{"Hard",10-10}]に等しい.
- 閾値指定 tspec は{tfun,pars}の形式で行う.
- tfun の可能な名前と位置
- 以下は使用可能な閾値関数 tfun およびそのパラメータ(入力データ
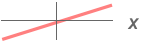 を使用する)である:
を使用する)である: -
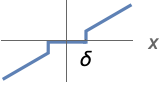
{"Hard",δ} ![ 0 TemplateBox[{x}, Abs]<=delta; x TemplateBox[{x}, Abs]>delta; 0 TemplateBox[{x}, Abs]<=delta; x TemplateBox[{x}, Abs]>delta;](Files/Threshold.ja/3.png)
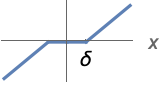
{"Soft",δ} ![ 0 TemplateBox[{x}, Abs]<=delta; sgn(x) (TemplateBox[{x}, Abs]-delta) TemplateBox[{x}, Abs]>delta; 0 TemplateBox[{x}, Abs]<=delta; sgn(x) (TemplateBox[{x}, Abs]-delta) TemplateBox[{x}, Abs]>delta;](Files/Threshold.ja/5.png)
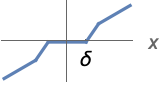
{"Firm",δ,r,p} ![ 0 TemplateBox[{x}, Abs]<=delta-delta p r; 1/(delta r)sgn(x) (delta+delta r-delta p r) (TemplateBox[{x}, Abs]-delta+delta p r) delta-delta p r<TemplateBox[{x}, Abs]<=delta+delta (-p) r+delta r; x TemplateBox[{x}, Abs]>delta+delta (-p) r+delta r; 0 TemplateBox[{x}, Abs]<=delta-delta p r; 1/(delta r)sgn(x) (delta+delta r-delta p r) (TemplateBox[{x}, Abs]-delta+delta p r) delta-delta p r<TemplateBox[{x}, Abs]<=delta+delta (-p) r+delta r; x TemplateBox[{x}, Abs]>delta+delta (-p) r+delta r;](Files/Threshold.ja/7.png)
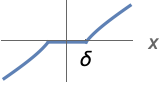
{"PiecewiseGarrote",δ} ![0 TemplateBox[{x}, Abs]<=delta; x-(delta^2)/x TemplateBox[{x}, Abs]>delta 0 TemplateBox[{x}, Abs]<=delta; x-(delta^2)/x TemplateBox[{x}, Abs]>delta](Files/Threshold.ja/9.png)
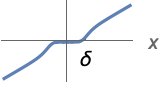
{"SmoothGarrote",δ,n} 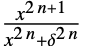
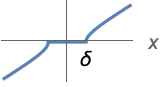
{"Hyperbola", 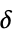 }
}![ 0 TemplateBox[{x}, Abs]<=delta; sgn(x) sqrt(x^2-delta^2) TemplateBox[{x}, Abs]>delta; 0 TemplateBox[{x}, Abs]<=delta; sgn(x) sqrt(x^2-delta^2) TemplateBox[{x}, Abs]>delta;](Files/Threshold.ja/14.png)
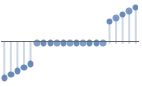
{"LargestValues",k} 最大 k データ点を保持する - すべての場合で
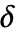 は正の数あるいは
は正の数あるいは 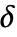 を計算するための閾値化関数 tfunc であると考えられる.各 tfunc[data]は正の数を返す.
を計算するための閾値化関数 tfunc であると考えられる.各 tfunc[data]は正の数を返す. - "Firm"のパラメータ条件は
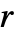 が正の実数で
が正の実数で 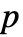 が0から1までの実数というものである.
が0から1までの実数というものである. - "SmoothGarrote"のパラメータ条件は
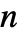 が正の機械整数というものである.
が正の機械整数というものである. - 閾値
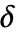 は次のメソッドを使って自動的に計算される.
は次のメソッドを使って自動的に計算される. -
{"BlackFraction",b} すべての画素を b の割合で黒くする "Cluster" クラスタ分散の最大化(大津アルゴリズム) "Entropy" ヒストグラムエントロピーの最大化(Kapurメソッド) "Mean" 平均レベルを閾値として使う "Median" 中央値の画素レベルを閾値として使う "MinimumError" Kittler–Illingworthの最小誤差閾値化法
例題
すべて開く すべて閉じるスコープ (14)
データ (7)
特性と関係 (7)
"Hard"閾値化は,絶対値が特定の閾値 ![]() より小さいデータ値をすべて0に設定する:
より小さいデータ値をすべて0に設定する:
"Hard"閾値化はChopに似ている:
"Firm"閾値化は"Hard"閾値化と"Soft"閾値化を折衷したものである:
"Firm"閾値化は"Hard"閾値化より分散が一様に小さい:
極限 β->∞では,"Firm"閾値化は"Soft"閾値化を行う:
極限 β->η では,"Firm"閾値化は"Hard"閾値化を行う:
これは"Firm"閾値化に似ており,パラメータが1つ(![]() )である利点がある:
)である利点がある:
テキスト
Wolfram Research (2010), Threshold, Wolfram言語関数, https://reference.wolfram.com/language/ref/Threshold.html (2012年に更新).
CMS
Wolfram Language. 2010. "Threshold." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/Threshold.html.
APA
Wolfram Language. (2010). Threshold. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Threshold.html
BibTeX
@misc{reference.wolfram_2025_threshold, author="Wolfram Research", title="{Threshold}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/Threshold.html}", note=[Accessed: 11-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_threshold, organization={Wolfram Research}, title={Threshold}, year={2012}, url={https://reference.wolfram.com/language/ref/Threshold.html}, note=[Accessed: 11-February-2026]}

