WaveletThreshold[dwd]
thresholds the detail wavelet coefficients in the DiscreteWaveletData object dwd.
WaveletThreshold[dwd,tspec]
thresholds the coefficients using the thresholding specification tspec.
WaveletThreshold[dwd,tspec,wind]
thresholds the wavelet coefficients given by the wavelet indices wind.


WaveletThreshold
WaveletThreshold[dwd]
thresholds the detail wavelet coefficients in the DiscreteWaveletData object dwd.
WaveletThreshold[dwd,tspec]
thresholds the coefficients using the thresholding specification tspec.
WaveletThreshold[dwd,tspec,wind]
thresholds the wavelet coefficients given by the wavelet indices wind.
Details


- WaveletThreshold[dwd] is effectively WaveletThreshold[dwd,"Universal"].
- WaveletThreshold[dwd,tspec,wind] indicates which wavelet coefficients to threshold, using the same index convention as described for DiscreteWaveletData.
- By default, thresholding is performed on detail coefficients at each refinement level.
- The threshold specification tspec can be of the form: tfun, {tfun,pars}.
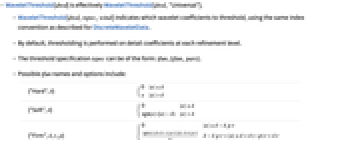
- Possible tfun names and options include:
-
{"Hard",δ} ![0 TemplateBox[{x}, Abs]<=delta; x TemplateBox[{x}, Abs]>delta 0 TemplateBox[{x}, Abs]<=delta; x TemplateBox[{x}, Abs]>delta](Files/WaveletThreshold.en/1.png)
{"Soft",δ} ![ 0 TemplateBox[{x}, Abs]<=delta; sgn(x) (TemplateBox[{x}, Abs]-delta) TemplateBox[{x}, Abs]>delta; 0 TemplateBox[{x}, Abs]<=delta; sgn(x) (TemplateBox[{x}, Abs]-delta) TemplateBox[{x}, Abs]>delta;](Files/WaveletThreshold.en/2.png)
{"Firm",δ,r,p} ![ 0 TemplateBox[{x}, Abs]<=delta-delta p r; (sgn(x) (delta+delta r-delta p r) (TemplateBox[{x}, Abs]-delta+delta p r))/(delta r) delta-delta p r<TemplateBox[{x}, Abs]<=delta+delta (-p) r+delta r; x TemplateBox[{x}, Abs]>delta+delta (-p) r+delta r; 0 TemplateBox[{x}, Abs]<=delta-delta p r; (sgn(x) (delta+delta r-delta p r) (TemplateBox[{x}, Abs]-delta+delta p r))/(delta r) delta-delta p r<TemplateBox[{x}, Abs]<=delta+delta (-p) r+delta r; x TemplateBox[{x}, Abs]>delta+delta (-p) r+delta r;](Files/WaveletThreshold.en/3.png)
{"PiecewiseGarrote",δ} ![0 TemplateBox[{x}, Abs]<=delta; x-(delta^2)/x TemplateBox[{x}, Abs]>delta 0 TemplateBox[{x}, Abs]<=delta; x-(delta^2)/x TemplateBox[{x}, Abs]>delta](Files/WaveletThreshold.en/4.png)
{"SmoothGarrote",δ,n} 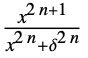
{"Hyperbola", 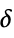 }
}![ 0 TemplateBox[{x}, Abs]<=delta; sgn(x) sqrt(x^2-delta^2) TemplateBox[{x}, Abs]>delta; 0 TemplateBox[{x}, Abs]<=delta; sgn(x) sqrt(x^2-delta^2) TemplateBox[{x}, Abs]>delta;](Files/WaveletThreshold.en/7.png)
{"LargestCoefficients",k} keep the largest k coefficients - In all cases
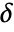 is assumed to be a positive number or a thresholding function tfunc to compute
is assumed to be a positive number or a thresholding function tfunc to compute 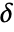 . Each tfunc[coefi,windi] should return a positive number.
. Each tfunc[coefi,windi] should return a positive number. - The parameter conditions for "Firm" are that
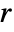 is a positive real and
is a positive real and 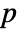 a positive real number between 0 and 1.
a positive real number between 0 and 1. - The parameter conditions for "SmoothGarrotte" are to have
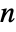 be a positive real number.
be a positive real number. - The threshold
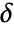 can be automatically computed using the following methods:
can be automatically computed using the following methods: -
Automatic "Universal" thresholding value {"FDR",α} false discovery rate at significance level α "GCV" minimizes generalized cross-validation function "GCVLevel" "GCV" performed at each level "SURE" Stein's unbiased risk estimate "SUREHybrid" combination of "SURE" and "Universal" thresholding "SURELevel" "SURE" performed at each level "Universal" Donoho and Johnstone's universal threshold "UniversalLevel" "Universal" performed at each level - The parameter conditions for {"FDR",α} are that α should be a number between 0 and 1. By default "FDR" is equivalent to {"FDR",0.05}.
- The following short tspec forms can be used:
-
"FDR" {"Soft",{"FDR",0.05}} "GCV" {"Soft","GCV"} "GCVLevel" {"Soft","GCVLevel"} "SURE" {"Hard","SURE"} "SURELevel" {"Hard","SURELevel"} "SUREShrink" {"Soft","SURE"} "Universal" {"Hard","Universal"} "UniversalLevel" {"Hard","UniversalLevel"} "VisuShrink" {"Soft","Universal"} "VisuShrinkLevel" {"Soft","UniversalLevel"}
Examples
open all close allBasic Examples (2)
DiscreteWaveletTransform of noisy data:
Smooth data by thresholding wavelet coefficients:
Compare original and smoothed data:
Remove noise from a color image:
Threshold wavelet coefficients:
Synthesize smoothed image using InverseWaveletTransform and compare with original:
Scope (12)
Basic Uses (4)
WaveletThreshold operates on a DiscreteWaveletData object:
The result is a new DiscreteWaveletData object representing thresholded coefficients:
Use specific threshold function:
Also specify how to choose threshold value:
Inverse transform and compare:
Visualize the effect on wavelet coefficients:
Compare using WaveletListPlot:
Perform thresholding on specific wavelet indexes:
By default only the detail coefficients are thresholded:
Use Automatic to threshold coefficients used in the inverse transform:
Use All to threshold all coefficients:
Use {wind1,wind2,…} to fully control which coefficients to threshold:
Thresholding Methods (8)
Smooth noisy data using automatic thresholding methods:
Compare all named automatic thresholding methods tspec:
Choose specific thresholding function tfun to apply:
Reconstruct data from thresholded coefficients with automatically chosen threshold value:
Use a named method to automatically compute the threshold value ![]() :
:
Reconstruct data after "Soft" thresholding with various threshold value selection methods:
Use a specific numerical threshold value ![]() :
:
The best smoothing occurs for threshold values ![]() that are similar to the scale of the noise:
that are similar to the scale of the noise:
Use a function to compute a threshold value ![]() :
:
Threshold all coefficients below the standard deviation:
Plot the effect of thresholding function tfun on coefficient values ranging from -0.5 to 0.5:
Apply thresholding separately at each refinement level to data varying on different scales:
Different methods for selecting separate threshold values at each level:
Compare with methods that choose one threshold value for all levels:
Perform thesholding by specifying a function and wavelet index to compute ![]() :
:
Threshold all detail coefficients below the standard deviation:
Generalizations & Extensions (1)
Use FindThreshold to compute thresholding values:
Specifying a thresholding function computes level-dependent thresholding values:
Applications (8)
Automatic Denoising (2)
Image Effects (1)
Benchmarking Thresholding Methods (2)
Plot the noise subtracted by different thresholding functions tfun with automatic threshold value:
Subtract smoothed data from original data (giving a noise model):
Compare performance of automatic thresholding methods when smoothing noisy data:
Quantify performance using SNR (signal-to-noise ratio) and peak SNR in decibels (dB):
Smooth by applying thresholding method th to detail coefficients {___,1}:
Compare all named automatic thresholding methods; higher value is better:
Computing Thresholding Values (3)
"Universal" thresholding value:
Perform a LiftingWaveletTransform:
The mean absolute deviation is computed using detail coefficients at first refinement level {1}:
Compute universal threshold value ![]() as
as ![]() and perform a "Hard" threshold:
and perform a "Hard" threshold:
Use WaveletThreshold to compute the "Universal" threshold value:
Perform a LiftingWaveletTransform:
Compute "SURE" threshold values ![]() :
:
Use WaveletThreshold to compute "SURE" threshold value:
Perform a LiftingWaveletTransform:
For each wavelet coefficient ![]() , find its two-sided
, find its two-sided ![]() -value
-value ![]() :
:
Order the ![]() according to their size
according to their size ![]() . Find
. Find ![]() , where
, where ![]() is the significance level:
is the significance level:
Use WaveletThreshold to compute "FDR" threshold value:
Properties & Relations (9)
Thresholding functions approach Identity for small threshold values ![]() :
:
"Hard" thresholding is similar to Chop:
Data values with absolute value below threshold ![]() are set to 0:
are set to 0:
"Soft" thresholding performs a shrinking operation:
Data values below a certain threshold ![]() are set to 0; those above
are set to 0; those above ![]() are "shrunk" by
are "shrunk" by ![]() :
:
Parameter ![]() (
(![]() ) controls the range over which firm thresholding interpolates between 0 and Identity. Parameter
) controls the range over which firm thresholding interpolates between 0 and Identity. Parameter ![]() (
(![]() ) controls where
) controls where ![]() lies between
lies between ![]() and
and ![]() , with
, with ![]() by default:
by default:
"Firm" thresholding is a compromise between "Hard" and "Soft" thresholding:
"Firm" thresholding has uniformly smaller variance than "Hard" thresholding:
In the limit ![]() , "Firm" threshold performs "Soft" thresholding:
, "Firm" threshold performs "Soft" thresholding:
In the limit ![]() , "Firm" threshold performs "Hard" thresholding:
, "Firm" threshold performs "Hard" thresholding:
"PiecewiseGarrote" thresholding:
This is similar to "Firm" thresholding with the advantage of having a single parameter ![]() :
:
In the limit ![]() , "SmoothGarotte" goes to "Hard" thresholding:
, "SmoothGarotte" goes to "Hard" thresholding:
Use WaveletMapIndexed to perform "Hard" thresholding:
Possible Issues (3)
Using "Hard" thresholding function with "GCV" thresholding value:
Noise coefficients may pass through "Hard" thresholding:
"Soft" thresholding function shrinks these spurious peaks:
The noise estimate is computed based on first-level detail coefficients:
A warning is generated if the estimated noise level is 0:
WaveletThreshold does not operate on non-numeric wavelet coefficients:
Related Guides
History
Text
Wolfram Research (2010), WaveletThreshold, Wolfram Language function, https://reference.wolfram.com/language/ref/WaveletThreshold.html.
CMS
Wolfram Language. 2010. "WaveletThreshold." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletThreshold.html.
APA
Wolfram Language. (2010). WaveletThreshold. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaveletThreshold.html
BibTeX
@misc{reference.wolfram_2025_waveletthreshold, author="Wolfram Research", title="{WaveletThreshold}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WaveletThreshold.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_waveletthreshold, organization={Wolfram Research}, title={WaveletThreshold}, year={2010}, url={https://reference.wolfram.com/language/ref/WaveletThreshold.html}, note=[Accessed: 28-February-2026]}