StationaryWaveletTransform[data]
gives the stationary wavelet transform (SWT) of an array of data.
StationaryWaveletTransform[data,wave]
gives the stationary wavelet transform using the wavelet wave.
StationaryWaveletTransform[data,wave,r]
gives the stationary wavelet transform using r levels of refinement.




StationaryWaveletTransform
StationaryWaveletTransform[data]
gives the stationary wavelet transform (SWT) of an array of data.
StationaryWaveletTransform[data,wave]
gives the stationary wavelet transform using the wavelet wave.
StationaryWaveletTransform[data,wave,r]
gives the stationary wavelet transform using r levels of refinement.
Details and Options



- StationaryWaveletTransform is similar to DiscreteWaveletTransform except that no subsampling occurs at any refinement level and the resulting coefficient arrays all have the same dimensions as the original data.
- StationaryWaveletTransform gives a DiscreteWaveletData object.
- Properties of the DiscreteWaveletData dwd can be found using dwd["prop"], and a list of available properties can be found using dwd["Properties"].
- The data can be any of the following:
-
list arbitrary-rank numerical array image arbitrary Image object audio an Audio or sampled Sound object - The possible wavelets wave include:
-
BattleLemarieWavelet[…] Battle–Lemarié wavelets based on B-spline BiorthogonalSplineWavelet[…] B-spline-based wavelet CoifletWavelet[…] symmetric variant of Daubechies wavelets DaubechiesWavelet[…] the Daubechies wavelets HaarWavelet[…] classic Haar wavelet MeyerWavelet[…] wavelet defined in the frequency domain ReverseBiorthogonalSplineWavelet[…] B-spline-based wavelet (reverse dual and primal) ShannonWavelet[…] sinc function-based wavelet SymletWavelet[…] least asymmetric orthogonal wavelet - The default wave is HaarWavelet[].
- With higher settings for the refinement level r, larger-scale features are resolved.
- The default refinement level r is given by
![TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor] TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor]](Files/StationaryWaveletTransform.en/1.png) , where
, where 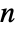 is the minimum dimension of data. »
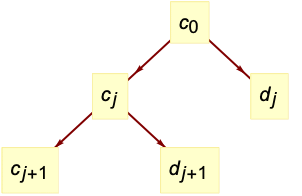
is the minimum dimension of data. » - The tree of wavelet coefficients at level
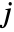 consists of coarse coefficients
consists of coarse coefficients 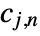 and detail coefficients
and detail coefficients 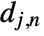 , with
, with 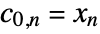 representing the input data.
representing the input data. - The forward transform is given by
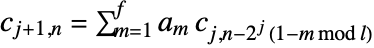 and
and 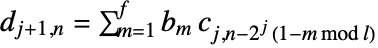 , where
, where 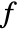 is the filter length for the corresponding wspec and
is the filter length for the corresponding wspec and 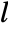 is the length of input data. »
is the length of input data. » - The inverse transform is given by
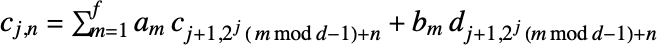 . »
. » - The
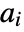 are lowpass filter coefficients and
are lowpass filter coefficients and 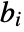 are highpass filter coefficients that are defined for each wavelet family.
are highpass filter coefficients that are defined for each wavelet family. - The dimensions of
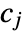 and
and 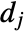 are the same as input data dimensions.
are the same as input data dimensions. - The following options can be given:
-
Method Automatic method to use WorkingPrecision MachinePrecision precision to use in internal computations - StationaryWaveletTransform uses periodic padding of data.
- InverseWaveletTransform gives the inverse transform.
Examples
open all close allBasic Examples (3)
Compute a stationary wavelet transform using the HaarWavelet:
Use Normal to view all coefficients:
Use dwd[…,"Audio"] to extract coefficient signals:
Verify lengths of all coefficient signals:
Compute the inverse transform:
Transform an Image object:
Scope (34)
Basic Uses (6)
Compute a stationary wavelet transform:
The resulting DiscreteWaveletData represents a tree of transform coefficients:
The inverse transform reconstructs the input:
Useful properties can be extracted from the DiscreteWaveletData object:
Get a full list of properties:
Get data and coefficient dimensions:
Use Normal to get all wavelet coefficients explicitly:
Also use All as an argument to get all coefficients:
Use Automatic to get only the coefficients used in the inverse transform:
Use the "TreeView" or "IndexMap" to find out what wavelet coefficients are available:
Extract specific coefficient arrays:
Extract several wavelet coefficients corresponding to the list of wavelet index specifications:
Extract all coefficients whose wavelet indexes match a pattern:
The Automatic coefficients are used by default in functions like WaveletListPlot:
Use a higher refinement level to increase the frequency resolution:
With a smaller refinement level, more of the signal energy is left in {0,0,0}:
With further refinement, {0,0,0} is resolved into further components:
Wavelet Families (10)
Compute the stationary wavelet transform using different wavelet families:
Use different families of wavelets to capture different features:
HaarWavelet (default):
Vector Data (6)
Plot the coefficients over a common horizontal axis using WaveletListPlot:
Plot against a common vertical axis:
Visualize coefficients as a function of time and refinement level using WaveletScalogram:
The coefficient indexes appear as tooltips when the mouse pointer is moved over a coefficient:
All coefficients are small except coarse coefficients {0,0,…}:
Data oscillating at the highest resolvable frequency (Nyquist frequency):
Only the first detail coefficient {1} is nonzero:
Data with large discontinuities:
Coarse coefficients {0,…} have the same large-scale structure as the data:
Detail coefficients are sensitive to discontinuities:
Data with both spatial and frequency structure:
Coarse coefficients {0,…} track the local mean of the data:
The first detail coefficient identifies the oscillatory region:
Matrix Data (5)
Compute a two-dimensional stationary wavelet transform:
View the tree of wavelet coefficients:
Inverse transform to get back the original signal:
Use dwd[…,"MatrixPlot"] to visualize each coefficient as a MatrixPlot:
Visualize wavelet coefficients at higher refinement levels:
In two dimensions, the vector of filtering operations in each direction can be computed:
Interpreting these vectors as binary digit expansions, you get wavelet index numbers:
Get the lowpass and highpass filters for a Haar wavelet:
The resulting 2D filters are outer products of filters in the two directions:
Wavelet transform of step data:
Data with a vertical discontinuity:
Only the vertical detail coefficients, wavelet index {…,1}, are nonzero:
Data with horizontal discontinuity:
Only the horizontal detail coefficients, wavelet index {…,2}, are nonzero:
Array Data (2)
Compute a three-dimensional stationary wavelet transform:
Tree view of all coefficients:
Inverse transform to get back the original signal:
Wavelet transform of a three-dimensional cross array:
Visualize wavelet coefficients:
Energy of the original data is conserved within the transformed coefficients:
Image Data (2)
Transform an Image object:
The inverse transform yields a reconstructed Image object:
Wavelet coefficients are normally given as arrays of data for each image channel:
Number of channels and dimensions of the original image are the same:
Get all coefficients as Image objects instead of arrays of data:
Get raw Image objects with no rescaling of color levels:
Get the inverse transform of the {0,1} coefficient as an Image object:
Sound Data (3)
Transform a Sound object:
The inverse transform yields a reconstructed Sound object:
By default, coefficients are given as lists of data for each sound channel:
Number of channels and data length in the original sound are the same:
Get the {0,1} coefficient as a Sound object:
Inverse transform of {0,0,1} coefficient as a Sound object:
Browse all coefficients using a MenuView:
Generalizations & Extensions (3)
StationaryWaveletTransform works on arrays of symbolic quantities:
Inverse transform recovers the input exactly:
Specify any internal working precision:
Options (3)
WorkingPrecision (3)
By default, WorkingPrecision->MachinePrecision is used:
Use higher-precision computation:
Use WorkingPrecision->∞ for exact computation:
Applications (3)
Inverse Halftoning (1)
A simple wavelet-based inverse halftoning:
Apply GaussianFilter on the detail coefficients:
Numerical Differentiation (1)
Differentiate noisy data using wavelet transform:
Translation-Rotation-Transform (TRT) is used to reduce boundary effects by subtracting a linear component from the input signal:
Since HaarWavelet has one vanishing moment, choose it to perform a wavelet transform on ![]() :
:
Detail coefficients give the differentiation of the data. Coefficients at refinement level 4 are chosen to minimize noise:
Rescale the differentiated values:
Compare wavelet-based numerical differentiation with exact differentiation:
Compare with standard Wolfram Language numerical differentiation:
Image Fusion (1)
Add texture to an existing image:
Perform wavelet transform on both images:
Combine detail coefficients of the two images by taking their mean:
Append the coarse coefficient of the first image:
Construct a new DiscreteWaveletData of the combined wavelet coefficients:
Properties & Relations (12)
StationaryWaveletPacketTransform computes the full tree of wavelet coefficients:
StationaryWaveletTransform computes a subset of the full tree of coefficients:
DiscreteWaveletTransform coefficients halve in length with each level of refinement:
Rotated data gives different coefficients:
StationaryWaveletTransform coefficients have the same length as the original data:
Rotated data gives rotated coefficients:
The default refinement is given by ![]() :
:
The energy norm is conserved for orthogonal wavelet families:
The energy norm is approximately conserved for biorthogonal wavelet families:
The mean of the data is captured at the maximum refinement level of the transform:
Extract the coefficient for the maximum refinement level:
The sum of inverse transforms from individual coefficient arrays gives the original data:
Individually inverse transform each wavelet coefficient array:
The sum gives the original data:
Compute stationary wavelet coefficients for periodic data:
Coarse coefficients at level ![]() are given by
are given by ![]() :
:
Detail coefficients at level ![]() are given by
are given by ![]() :
:
Compute partial stationary inverse wavelet transform:
Coarse coefficients at level ![]() are given:
are given:
Detail coefficients at level ![]() are given:
are given:
Inverse wavelet transform at level ![]() is given by
is given by ![]() :
:
Reconstruct coarse coefficients {0,0} at refinement level ![]() :
:
Reconstruct coarse coefficients {0} at refinement level ![]() :
:
Compute a Haar stationary wavelet transform in one dimension:
Compute {0} and {1} wavelet coefficients:
Compare with DiscreteWaveletPacketTransform:
In two dimensions, a separate filter is applied in each dimension:
Lowpass and highpass filters for a Haar wavelet:
Haar wavelet transform of matrix data:
Compare with DiscreteWaveletPacketTransform using HaarWavelet:
Image channels are transformed individually:
Combine {0} coefficients of separately transformed image channels:
Compare with {0} coefficient of StationaryWaveletTransform of the original image:
Related Guides
Text
Wolfram Research (2010), StationaryWaveletTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/StationaryWaveletTransform.html (updated 2017).
CMS
Wolfram Language. 2010. "StationaryWaveletTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/StationaryWaveletTransform.html.
APA
Wolfram Language. (2010). StationaryWaveletTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StationaryWaveletTransform.html
BibTeX
@misc{reference.wolfram_2025_stationarywavelettransform, author="Wolfram Research", title="{StationaryWaveletTransform}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/StationaryWaveletTransform.html}", note=[Accessed: 13-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_stationarywavelettransform, organization={Wolfram Research}, title={StationaryWaveletTransform}, year={2017}, url={https://reference.wolfram.com/language/ref/StationaryWaveletTransform.html}, note=[Accessed: 13-January-2026]}