MatrixPlot[m]
generates a plot that gives a visual representation of the values of elements in a matrix.




MatrixPlot
MatrixPlot[m]
generates a plot that gives a visual representation of the values of elements in a matrix.
Details and Options

- MatrixPlot[m] by default arranges successive rows of m down the page and successive columns across, just as a matrix would normally be formatted.
- MatrixPlot by default displays zero values as white, with negative values tending to be bluish and positive values reddish.
- MatrixPlot has the same options as ArrayPlot, with the following changes: [List of all options]
-
ClippingStyle Automatic how to show clipped values Frame True whether to draw a frame around the plot FrameTicks All what ticks to include on the frame MaxPlotPoints Automatic the maximum number of points to include - PlotRange->r specifies that only those aij between -r and +r should be shown.
- With the default setting ColorFunctionScaling->True, scaling is done based on a mixture of relative value and ranking for each matrix element. The final scaled value always lies between 0 and 1, with scaled value 0.5 corresponding to matrix element value 0.
- With the default setting MaxPlotPoints->Automatic, sufficiently large or sparse matrices are downsampled so that their structure is visible in the plot generated by MatrixPlot.
- MatrixPlot works with SparseArray objects.
-
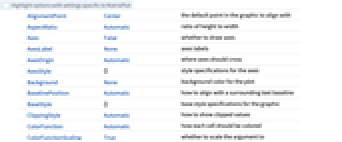
AlignmentPoint Center the default point in the graphic to align with AspectRatio Automatic ratio of height to width Axes False whether to draw axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic ClippingStyle Automatic how to show clipped values ColorFunction Automatic how each cell should be colored ColorFunctionScaling True whether to scale the argument to ColorFunction ColorRules Automatic rules for determining colors from values ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool DataRange All the range of 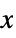 and
and 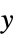 values to assume
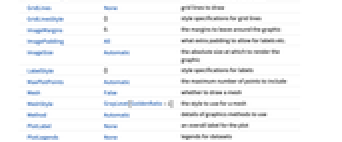
values to assume DataReversed False whether to reverse the order of rows Epilog {} primitives rendered after the main plot FormatType TraditionalForm the default format type for text Frame True whether to draw a frame around the plot FrameLabel None labels for rows and columns FrameStyle {} style specifications for the frame FrameTicks All what ticks to include on the frame FrameTicksStyle {} style specifications for frame ticks GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic LabelStyle {} style specifications for labels MaxPlotPoints Automatic the maximum number of points to include Mesh False whether to draw a mesh MeshStyle GrayLevel[GoldenRatio-1] the style to use for a mesh Method Automatic details of graphics methods to use PlotLabel None an overall label for the plot PlotLegends None legends for datasets PlotRange All the range of values to plot PlotRangeClipping False whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotTheme $PlotTheme overall theme for the plot PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RotateLabel True whether to rotate y labels on the frame TargetUnits Automatic units to display in the plot Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks
List of all options

Examples
open all close allBasic Examples (4)
Scope (19)
Data (10)
Plot a nonrectangular "matrix", with missing entries transparent:
Negative entries are shown in cool colors, positive entries in warm colors, and zeros in white:
Entries near zero are shown in a shade of gray; entries very close to zero may be shown in white:
Complex numbers are shown based on their real parts:
None is interpreted as a missing value and displayed using transparency:
Symbolic values other than None are shown in dark red:
Colors are shown darker for very sparse matrices to make entries more visible:
Show a matrix with irrational and arbitrary-precision entries:
Presentation (9)
Give explicit color directives to specify colors for individual cells:
Use a black-and-white color function to highlight the sparse structure of a matrix:
Use a custom color function with blue colors for negative values and red colors for positive values:
Use ColorRules to color different values:
Use both ColorRules and ColorFunction to color elements, giving priority to ColorRules:
Options (33)
Background (2)
Background is normally visible only around the edges:
The background "shows through" whenever an explicit entry is None:
ClippingStyle (3)
By default, the clipped values are colored vibrant red and blue:
Use explicit colors for the clipped values:
Use None to indicate no style, showing the background in those cells:
ColorFunction (5)
Use an explicit color function:
Use a pure function as the color function:
Use a named color gradient from ColorData:
If the color function is undefined for some value, then a dark red is substituted:
In this case, the color is defined for all the values:
For complex matrices, the real part is used for the color function:
ColorFunctionScaling (4)
By default, a nonlinear scaling of entries is used to differentiate values over a wide range:
With ColorFunctionScaling->False, entries are not scaled:
With ColorFunctionScaling->False, MatrixPlot behaves like ArrayPlot:
ColorFunctionScaling has no effect on ColorRules:
ColorRules (6)
Specify color rules for explicit values or patterns:
Implement a "default color" by adding a rule for _:
The array can contain symbolic values:
Use any patterns in ColorRules:
Rules are used in the order given:
ColorRules can be used together with ColorFunction and has higher priority:
MaxPlotPoints (1)
By default, automatic methods are used to downsample large and/or sparse matrices:
Without downsampling, the entries are less visible:
Explicitly set downsampling values for MaxPlotPoints:
The visual appearance in the resulting plot is also affected by the choice of ColorFunction:
Mesh (3)
PlotRange (3)
Plot only elements with values from 0 to 1; clip the rest:
The first two entries in PlotRange specify the range of rows and columns to include:
Applications (3)
Properties & Relations (6)
MatrixPlot colors negative entries with cool colors and positive entries with warm colors:
ArrayPlot uses gray scale:
MatrixPlot rescales the matrix entries to differentiate values over a wide range:
Without rescaling, fewer elements can be differentiated:
Use ReliefPlot for medical and geographic data:
Use ListDensityPlot for structured or unstructured data sampled from continuous densities:
Use ArrayPlot3D for 3D arrays of data:
Use GraphPlot for visualizing adjacency matrices:
Possible Issues (2)
Using MaxPlotPoints may result in artifacts not actually present in the original data:
With a small MaxPlotPoints option value, all entries become nonzero:
Neat Examples (1)
Plot the Sin function at integer points:
See Also
Related Guides
Text
Wolfram Research (2007), MatrixPlot, Wolfram Language function, https://reference.wolfram.com/language/ref/MatrixPlot.html (updated 2014).
CMS
Wolfram Language. 2007. "MatrixPlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/MatrixPlot.html.
APA
Wolfram Language. (2007). MatrixPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MatrixPlot.html
BibTeX
@misc{reference.wolfram_2025_matrixplot, author="Wolfram Research", title="{MatrixPlot}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MatrixPlot.html}", note=[Accessed: 08-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_matrixplot, organization={Wolfram Research}, title={MatrixPlot}, year={2014}, url={https://reference.wolfram.com/language/ref/MatrixPlot.html}, note=[Accessed: 08-March-2026]}