LiftingWaveletTransform[data]
gives the lifting wavelet transform (LWT) of an array of data.
LiftingWaveletTransform[data,wave]
gives the lifting wavelet transform using the wavelet wave.
LiftingWaveletTransform[data,wave,r]
gives the lifting wavelet transform using r levels of refinement.




LiftingWaveletTransform
LiftingWaveletTransform[data]
gives the lifting wavelet transform (LWT) of an array of data.
LiftingWaveletTransform[data,wave]
gives the lifting wavelet transform using the wavelet wave.
LiftingWaveletTransform[data,wave,r]
gives the lifting wavelet transform using r levels of refinement.
Details and Options
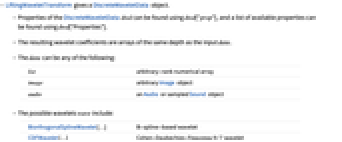


- LiftingWaveletTransform gives a DiscreteWaveletData object.
- Properties of the DiscreteWaveletData dwd can be found using dwd["prop"], and a list of available properties can be found using dwd["Properties"].
- The resulting wavelet coefficients are arrays of the same depth as the input data.
- The data can be any of the following:
-
list arbitrary-rank numerical array image arbitrary Image object audio an Audio or sampled Sound object - The possible wavelets wave include:
-
BiorthogonalSplineWavelet[…] B-spline-based wavelet CDFWavelet[…] Cohen-Daubechies-Feauveau 9/7 wavelet CoifletWavelet[…] symmetric variant of Daubechies wavelets DaubechiesWavelet[…] the Daubechies wavelets HaarWavelet[…] classic Haar wavelet ReverseBiorthogonalSplineWavelet[…] B-spline-based wavelet (reverse dual and primal) SymletWavelet[…] least asymmetric orthogonal wavelet - The default wave is HaarWavelet[].
- With higher settings for the refinement level r, larger scale features are resolved.
- With refinement level r, LiftingWaveletTransform internally pre-pads data so that each dimension is a multiple of
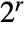 . The padding values used for pre-padding are given by the setting of the Padding option. »
. The padding values used for pre-padding are given by the setting of the Padding option. » - With refinement level Full, r is given by
![TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor] TemplateBox[{{{InterpretationBox[{log, _, DocumentationBuild`Utils`Private`Parenth[2]}, Log2, AutoDelete -> True], (, n, )}, +, {1, /, 2}}}, Floor]](Files/LiftingWaveletTransform.en/2.png) .
. - The default levels of refinement r are given by
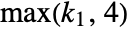 , where
, where 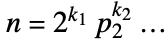 is the integer factorization of the length of data. For multi-dimensional data, the same computation is done for each dimension and the resulting minimum refinement level is used. »
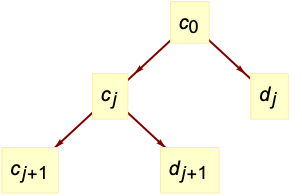
is the integer factorization of the length of data. For multi-dimensional data, the same computation is done for each dimension and the resulting minimum refinement level is used. » - The tree of wavelet coefficients at level
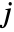 consists of coarse coefficients
consists of coarse coefficients 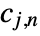 and detail coefficients
and detail coefficients 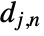 , with
, with 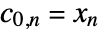 representing the input data.
representing the input data. - The dimensions of
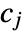 and
and 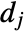 are given by
are given by 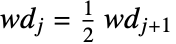 , where
, where 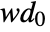 is given by
is given by ![2^r TemplateBox[{{l, /, {2, ^, r}}}, Ceiling] 2^r TemplateBox[{{l, /, {2, ^, r}}}, Ceiling]](Files/LiftingWaveletTransform.en/14.png) , where
, where 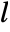 is the input data dimension. »
is the input data dimension. » - The following options can be given:
-
Method Automatic method to use Padding "Periodic" how to extend data beyond boundaries WorkingPrecision MachinePrecision precision to use in internal computations - The settings for Padding include "Periodic" for periodic repetition of the dataset in each dimension and
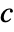 for constant padding.
for constant padding. - With the setting Method->"IntegerLifting", integer data will transform to integer coefficients, in which case input image data of type "Real" is converted to type "Byte".
- InverseWaveletTransform gives the inverse transform.
Examples
open all close allBasic Examples (3)
Compute a lifting wavelet transform using the HaarWavelet:
Use Normal to view all coefficients:
Use dwd[…,"Audio"] to extract coefficient signals:
Compute the inverse transform:
Transform an Image object:
Scope (33)
Basic Uses (7)
Compute a lifting wavelet transform:
The resulting DiscreteWaveletData represents a tree of transform coefficients:
The inverse transform reconstructs the input:
Compute an integer lifting wavelet transform:
Use Normal to view all integer coefficients:
The inverse transform reconstructs the input:
Useful properties can be extracted from the DiscreteWaveletData object:
Get a full list of properties:
Get data and coefficient dimensions:
Use Normal to get all wavelet coefficients explicitly:
Also use All as an argument to get all coefficients:
Use Automatic to get only the coefficients used in the inverse transform:
Use the "TreeView" or "WaveletIndex" to find out what wavelet coefficients are available:
Extract specific coefficient arrays:
Extract several wavelet coefficients corresponding to the list of wavelet index specifications:
Extract all coefficients whose wavelet indexes match a pattern:
The Automatic coefficients are used by default in functions like WaveletListPlot:
Use a higher refinement level to increase the frequency resolution:
With a smaller refinement level, more of the signal energy is left in {0,0,0}:
With further refinement, {0,0,0} is resolved into further components:
Wavelet Families (8)
Compute the discrete wavelet transform using different wavelet families:
Use different families of wavelets to capture different features:
HaarWavelet (default):
ReverseBiorthogonalSplineWavelet:
Use LiftingFilterData as an input to LiftingWaveletTransform:
Vector Data (6)
Plot the coefficients over a common horizontal axis using WaveletListPlot:
Plot against a common vertical axis:
Visualize coefficients as a function of time and refinement level using WaveletScalogram:
The coefficient indexes appear as tooltips when the mouse pointer is moved over a coefficient:
All coefficients are small except coarse coefficients {0,0,…}:
Data oscillating at the highest resolvable frequency (Nyquist frequency):
Only the first detail coefficient {1} is not small:
Data with large discontinuities:
Coarse coefficients {0,…} have the same large scale structure as the data:
Detail coefficients are sensitive to discontinuities:
Data with both spatial and frequency structure:
Coarse coefficients {0,…} track the local mean of the data:
The first detail coefficient identifies the oscillatory region:
Matrix Data (4)
Compute a two-dimensional lifting wavelet transform:
View the tree of wavelet coefficients:
Inverse transform to get back the original signal:
Use WaveletMatrixPlot to visualize the different wavelet coefficients:
In two dimensions, the vector of filtering operations in each direction can be computed:
Interpreting these vectors as binary digit expansions, we get wavelet index numbers:
Wavelet transform of step data:
Data with a vertical discontinuity:
Only the vertical detail coefficients, wavelet index {…,1}, are nonzero:
Data with horizontal discontinuity:
Only the horizontal detail coefficients, wavelet index {…,2}, are nonzero:
Data with diagonal discontinuity:
Only the diagonal detail coefficients, wavelet index {…,3}, are nonzero:
Array Data (2)
Compute a three-dimensional lifting wavelet transform:
Tree view of all coefficients:
Inverse transform to get back the original signal:
Wavelet transform of a three-dimensional cross array:
Visualize wavelet coefficients:
Energy of the original data is conserved within the transformed coefficients:
Image Data (3)
Transform an Image object:
The inverse transform yields a reconstructed Image object:
Wavelet coefficients are normally given as lists of data for each image channel:
Get all coefficients as Image objects instead:
Get raw Image objects with no rescaling of color levels:
Get the inverse transform of the {0,1} coefficient as an Image object:
Plot coefficients used in inverse transform in a hierarchical grid using WaveletImagePlot:
Sound Data (3)
Transform a Sound object:
The inverse transform yields a reconstructed Sound object:
By default, coefficients are given as lists of data for each sound channel:
Get the {1} coefficient as a Sound object:
Inverse transform of {1} coefficient as a Sound object:
Browse all coefficients using a MenuView:
Generalizations & Extensions (3)
LiftingWaveletTransform works on arrays of symbolic quantities:
Inverse transform recovers the input exactly:
Specify any internal working precision:
Options (6)
Method (2)
Padding (1)
WorkingPrecision (3)
By default, WorkingPrecision->MachinePrecision is used:
Use higher-precision computation:
With numbers close to zero, accuracy is the better indicator of the number of correct digits:
Use WorkingPrecision->∞ for exact computation:
Applications (1)
Advanced Image Processing (1)
Preprocess images to improve performance of image processing functions:
Plot transformed image coefficients:
Extract vertical and diagonal components from the wavelet-transformed image and reconstruct:
Threshold image pixel values below 0.5:
With vertical components intensified, apply ImageLines:
Properties & Relations (11)
LiftingWaveletTransform and DiscreteWaveletTransform are closely related:
DWT is similar to LiftingWaveletTransform with extra coefficients needed for padding:
LiftingWaveletTransform coefficients halve in length with each level of refinement:
Rotated data give different coefficients:
StationaryWaveletTransform coefficients have the same length as the original data:
Rotated data give rotated coefficients:
The default refinement level is given by integer factorization of the length of data:
Odd length data is padded with zeros to make it even:
For a specified refinement level r, input data of length l is padded as Ceiling[l,2r]–l:
For input data of length 10 with 4 refinement levels, padding lengths are given:
ArrayPad is used to perform a padding operation:
For data with 10 rows and 15 columns with 3 refinement levels, padding in each dimension is given:
Compute dimensions of wavelet coefficients:
The dimensions of wavelet coefficients are given by ![]() , where
, where ![]() is the input data dimension:
is the input data dimension:
Compare ![]() dimensions with coefficient dimensions in dwd:
dimensions with coefficient dimensions in dwd:
The energy norm is conserved for orthogonal wavelet families:
The energy norm is approximately conserved for biorthogonal wavelet families:
The mean of the data is captured at the maximum refinement level of the transform:
Extract the coefficient for the maximum refinement level:
Compensate for the ![]() normalization at each refinement level:
normalization at each refinement level:
The sum of inverse transforms from individual coefficient arrays gives the original data:
Individually inverse transform each wavelet coefficient array:
The sum gives the original data:
Image channels are transformed individually:
Combine {0} coefficients of separately transformed image channels:
Compare with {0} coefficient of LiftingWaveletTransform of the original image:
Related Guides
Text
Wolfram Research (2010), LiftingWaveletTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/LiftingWaveletTransform.html (updated 2017).
CMS
Wolfram Language. 2010. "LiftingWaveletTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/LiftingWaveletTransform.html.
APA
Wolfram Language. (2010). LiftingWaveletTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LiftingWaveletTransform.html
BibTeX
@misc{reference.wolfram_2025_liftingwavelettransform, author="Wolfram Research", title="{LiftingWaveletTransform}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/LiftingWaveletTransform.html}", note=[Accessed: 07-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_liftingwavelettransform, organization={Wolfram Research}, title={LiftingWaveletTransform}, year={2017}, url={https://reference.wolfram.com/language/ref/LiftingWaveletTransform.html}, note=[Accessed: 07-March-2026]}