Threshold
Threshold[data]
通过将接近零的值替换为零,对 data 进行阈值处理.
Threshold[data,tspec]
使用阈值规范 tspec 对 data 进行阈值处理.
Threshold[image,…]
将 image 中较小的值替换为零.
Threshold[sound,…]
将 sound 中较小的值替换为零.
更多信息


- 阈值处理是一种数学分割运算,用于将特定区域中的值设置为零,有时也会减小区域外的值.
- Threshold 适用于任何阶的数据数组,以及二维和三维图像.
- Threshold[data] 等同于 Threshold[data,{"Hard",10-10}].
- 阈值规范 tspec 的格式可以为 {tfun,pars}.
- 可能的 tfun 名称和选项包括:
- 可用的阈值处理函数 tfun 及其参数有(使用输入数据
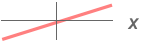 ):
): -
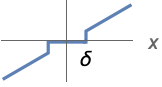
{"Hard",δ} ![ 0 TemplateBox[{x}, Abs]<=delta; x TemplateBox[{x}, Abs]>delta; 0 TemplateBox[{x}, Abs]<=delta; x TemplateBox[{x}, Abs]>delta;](Files/Threshold.zh/3.png)
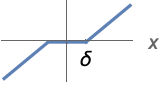
{"Soft",δ} ![ 0 TemplateBox[{x}, Abs]<=delta; sgn(x) (TemplateBox[{x}, Abs]-delta) TemplateBox[{x}, Abs]>delta; 0 TemplateBox[{x}, Abs]<=delta; sgn(x) (TemplateBox[{x}, Abs]-delta) TemplateBox[{x}, Abs]>delta;](Files/Threshold.zh/5.png)
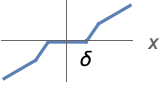
{"Firm",δ,r,p} ![ 0 TemplateBox[{x}, Abs]<=delta-delta p r; 1/(delta r)sgn(x) (delta+delta r-delta p r) (TemplateBox[{x}, Abs]-delta+delta p r) delta-delta p r<TemplateBox[{x}, Abs]<=delta+delta (-p) r+delta r; x TemplateBox[{x}, Abs]>delta+delta (-p) r+delta r; 0 TemplateBox[{x}, Abs]<=delta-delta p r; 1/(delta r)sgn(x) (delta+delta r-delta p r) (TemplateBox[{x}, Abs]-delta+delta p r) delta-delta p r<TemplateBox[{x}, Abs]<=delta+delta (-p) r+delta r; x TemplateBox[{x}, Abs]>delta+delta (-p) r+delta r;](Files/Threshold.zh/7.png)
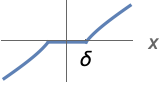
{"PiecewiseGarrote",δ} ![0 TemplateBox[{x}, Abs]<=delta; x-(delta^2)/x TemplateBox[{x}, Abs]>delta 0 TemplateBox[{x}, Abs]<=delta; x-(delta^2)/x TemplateBox[{x}, Abs]>delta](Files/Threshold.zh/9.png)
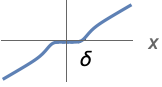
{"SmoothGarrote",δ,n} 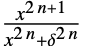
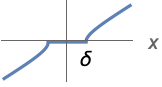
{"Hyperbola", 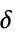 }
}![ 0 TemplateBox[{x}, Abs]<=delta; sgn(x) sqrt(x^2-delta^2) TemplateBox[{x}, Abs]>delta; 0 TemplateBox[{x}, Abs]<=delta; sgn(x) sqrt(x^2-delta^2) TemplateBox[{x}, Abs]>delta;](Files/Threshold.zh/14.png)
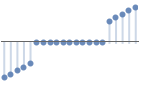
{"LargestValues",k} 保持最大的 k 数据点 - 在所有情况下
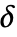 被假设为一个正数或用一个阈值函数 tfunc 来计算
被假设为一个正数或用一个阈值函数 tfunc 来计算 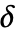 . 每个 tfunc[data] 应返回一个正数.
. 每个 tfunc[data] 应返回一个正数. - "Firm" 的参数条件是
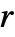 是正实数,
是正实数,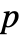 是 0 到 1 之间的实数.
是 0 到 1 之间的实数. - "SmoothGarrote" 的参数条件是
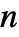 为正的机器整数.
为正的机器整数. - 可使用以下方法自动计算阈值
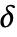 :
: -
{"BlackFraction",b} 将占所有像素比例为 b 的部分像素变为黑色 "Cluster" 聚类方差最大化(大津-Otsu 算法) "Entropy" 直方图熵最小化(Kapur 方法) "Mean" 使用均值作为阈值 "Median" 使用中位数像素级作为阈值 "MinimumError" Kittler–Illingworth 最小误差阈值方法
范例
打开所有单元关闭所有单元范围 (14)
Data (7)
属性和关系 (7)
"Hard" 阈值化将绝对值低于某个阈值 ![]() 的所有数据值设为 0:
的所有数据值设为 0:
"Hard" 阈值化类似于 Chop:
"Firm" 阈值化是 "Hard" 和 "Soft" 阈值化的一个折衷:
"Firm" 阈值化具有比 "Hard" 阈值化更小的方差:
当极限 β->∞,"Firm" 阈值化执行的是 "Soft" 阈值化:
当极限 β->η,"Firm" 阈值化执行的是 "Hard" 阈值化:
文本
Wolfram Research (2010),Threshold,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Threshold.html (更新于 2012 年).
CMS
Wolfram 语言. 2010. "Threshold." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2012. https://reference.wolfram.com/language/ref/Threshold.html.
APA
Wolfram 语言. (2010). Threshold. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Threshold.html 年