Tree

Tree[{subtree1,subtree2,…}]

子の部分木 subtreeiのリストがある木を表す．

Tree[key1subtree1,key2subtree2,…|>]

キーが keyiの連想として子を指定する．

Tree[data,subtrees]

根に data を含み子が subtrees で与えられる木を表す．

詳細とオプション

  • Treeオブジェクトは，根があり，順序があり，葉があるラベルが付いた木を表す．標準的な例として，XML，JSON，ファイルシステム，Wolfram言語のノートブックや式等が挙げられる．
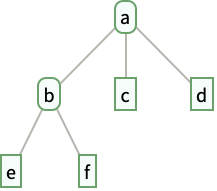
  • Tree[a,…]はノートブック内では根ノードがデータ a を持ち子ノードがデータ b, c, …を持つ木グラフのプロットとして表示される．
  • 木はノードの階層を同時に表現し，各ノードにXMLElement式やCell式のような一般的なデータを格納する．
  • Tree[data,subtrees]の subtrees は葉と解釈される他のTree式か一般的な式である．
  • Tree[…]は常にTree[data,subtrees]の構造を持つ標準形に変換される．
  • Tree[subtrees]はTree[Null,subtrees]に等しい．
  • Treeは，AtomQのような関数には生のオブジェクトとして扱われる．
  • data を含んでいるノードはTree[data,subtrees]として表される．
  • Tree[data,None]の形の木は葉と呼ばれる．その他の木はどれも，子のリストあるいは連想を含む内部ノードに対応するTree[data,{…}]あるいはTree[data,<|…|>]の形である．
  • TreeGraphは大域的に木を異なる頂点間の有向辺のリストとして表すGraphオブジェクトを返す．Treeはそれぞれが独立したデータ式を含むネストした部分木を表す．
  • 次は，個々の木の要素あるいはノードに影響するオプションである．
  • TreeElementLabel部分木の要素のラベル
    TreeElementLabelStyle部分木の要素のラベルのスタイル
    TreeElementLabelFunction部分木の要素のラベルを生成する
    TreeElementStyle部分木の要素のスタイル
    TreeElementStyleFunction部分木の要素のスタイルを生成する
    TreeElementCoordinates部分木の要素のサイズ
    TreeElementSize部分木の要素のサイズを生成する
    TreeElementSizeFunction部分木の要素のグラフィックス形状
    TreeElementShape部分木の要素のグラフィックス形状を生成する
    TreeElementShapeFunction部分木の要素の座標
  • 次は，個々の辺に影響するオプションである．
  • ParentEdgeLabel辺のラベルとその配置
    ParentEdgeLabelStyle辺のラベルのスタイル
    ParentEdgeLabelFunction辺のラベルを生成する
    ParentEdgeStyle辺のスタイル
    ParentEdgeStyleFunction辺のスタイルを生成する
    ParentEdgeShapeFunction辺のグラフィックス形状を生成する
  • 次は，ノードの省略に影響するオプションである．
  • MaxDisplayedChildren表示する子の最大数
  • 次は，木全体に影響するオプションである．
  • TreeLayout部分木と辺のレイアウトの仕方
  • TreeはGraphおよびGraphicsのすべてのオプションを取る．

例題

すべて開くすべて閉じる

例  (5)

2枚の葉がある木：

複数の葉がある木：

葉にデータのみがある木：

データとして別の木を含む木：

名前付きの辺がある木：

スコープ  (4)

子がない葉を表す：

子がない内側のノードを表す：

リストで子を指定する：

子を連想で指定する：

オプション  (11)

個々の木の要素のスタイル付け  (2)

生成された木要素のラベルを指定する：

部分木のラベルとスタイルをその位置によって指定する：

木全体のスタイル付け  (4)

すべての部分木のラベルとスタイルを指定する：

基本スタイルを指定する：

辺と木の両要素の辺のスタイルを指定する：

基本スタイルと個々の木の要素のスタイルを指定する：

木のレイアウトとグラフィックスオプション  (3)

根の向きを指定する：

名前付きの埋込みを指定する：

Graphicsオプションを指定する：

省略  (2)

根ノードのすべての子を表示する：

5つの子ノードを表示する：

すべてのノードについて子ノードを2つずつ表示する：

アプリケーション  (8)

XMLを記号XMLとしてインポートする：

タグ，属性，要素の階層から木を作成する：

XMLの木を記号XMLに変換する：

JSONを記号JSONとしてインポートする：

名前と値の階層から木を作成する：

JSONの木を記号JSONに変換する：

生命の木を作る：

子孫の木を作る：

ディレクトリ内のサブディレクトリとファイルの階層から木を作る：

TextElementオブジェクトを木に変換する関数を定義する：

TextElementの子要素を与える関数を定義する：

TextElementから"GrammaticalUnit"を抽出する関数を定義する：

特性とテキストの階層から木を作成する：

テキストの木をTextElementに変換する：

人口が10万人以上の米国の都市のリストを入手する：

都市をその測地位置によって階層的にクラスタ化したグラフを構築する：

クラスタ化した階層をGraphオブジェクトからTreeオブジェクトに変換する：

各葉について都市の測地位置を階層化クラスタリンググラフの指標から得る：

クラスタを表す各部分木について，子の空間的中央値を含む木を与える：

各葉の都市の位置と各クラスタの位置の空間中央値を使って測地位置の木を入手する：

測地位置の木の辺を米国の地図上に示す：

家系図を作る：

誕生日を与える連想を作る：

2人の人間を比較して第1子を設けた年齢が若い方をその子供と子供が生まれたときの当人の年齢とともに与える関数を定義する：

2人の兄弟を比較して，年長の方，両者の誕生日，彼らの子孫の中で最初に親になった年齢が最年少の者を与える関数を定義する：

ある人の子孫の中で．子が与えられた場合に最初に親になった年齢が最小の者を与える関数を定義する：

木の中で最初に親になった年齢が最小の者を，最初の子とその子が生まれたときの年齢とともに求める：

特性と関係  (6)

木のノードはデータを持たなくてもよい：

RulesTreeはTree式を返す：

頭部がTreeの式が有効なTreeオブジェクトかどうかチェックする：

次は有効なTreeオブジェクトではない：

次は無効なTree式をデータとして持つ子を含む有効なTreeオブジェクトである：

ExpressionTreeでTree式を構築する：

GraphTreeでTree式を構築する：

Wolfram Research (2021), Tree, Wolfram言語関数， https://reference.wolfram.com/language/ref/Tree.html （2022年に更新）.

テキスト

Wolfram Research (2021), Tree, Wolfram言語関数， https://reference.wolfram.com/language/ref/Tree.html （2022年に更新）.

CMS

Wolfram Language. 2021. "Tree." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Tree.html.

APA

Wolfram Language. (2021). Tree. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Tree.html

BibTeX

@misc{reference.wolfram_2024_tree, author="Wolfram Research", title="{Tree}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/Tree.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_tree, organization={Wolfram Research}, title={Tree}, year={2022}, url={https://reference.wolfram.com/language/ref/Tree.html}, note=[Accessed: 17-November-2024 ]}