TriangleWave[x]
gives a triangle wave that varies between ![]() and
and ![]() with unit period.
with unit period.
TriangleWave[{min,max},x]
gives a triangle wave that varies between min and max with unit period.


TriangleWave
TriangleWave[x]
gives a triangle wave that varies between ![]() and
and ![]() with unit period.
with unit period.
TriangleWave[{min,max},x]
gives a triangle wave that varies between min and max with unit period.
Details
- TriangleWave[x] is symmetric about
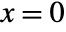 , and has value
, and has value 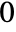 at
at 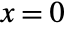 .
. - TriangleWave automatically threads over lists. »
Examples
open all close allBasic Examples (3)
Plot over a subset of the reals:
TriangleWave is a piecewise function over finite domains:
Scope (34)
Numerical Evaluation (5)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
TriangleWave threads over lists in the last argument:
Compute the elementwise values of an array using automatic threading:
Or compute the matrix TriangleWave function using MatrixFunction:
Specific Values (4)
Values of TriangleWave at fixed points:
Find a value of ![]() for which the TriangleWave[x]=0.5:
for which the TriangleWave[x]=0.5:
Visualization (4)
Plot the TriangleWave function:
Visualize scaled TriangleWave functions:
Visualize TriangleWave functions with different maximum and minimum values:
Plot TriangleWave in three dimensions:
Function Properties (11)
Function domain of TriangleWave:
It is restricted to real inputs:
Function range of TriangleWave[x]:
TriangleWave is periodic with period 1:
TriangleWave is an odd function:
The area under one period is zero:
TriangleWave is not an analytic function because it is singular at the half-integers:
TriangleWave[x] is neither nondecreasing nor nonincreasing:
TriangleWave is not injective:
TriangleWave[x] is not surjective:
TriangleWave[x] is neither non-negative nor non-positive:
TriangleWave is neither convex nor concave:
Differentiation and Integration (5)
First derivative with respect to ![]() :
:
Derivative of the two-argument form with respect to ![]() :
:
The second (and higher) derivatives are zero except at points where the derivative does not exist:
If a==b, TriangleWave[{a,b},x] is constant and its derivatives are zero everywhere:
Series Expansions (5)
Since TriangleWave is odd, FourierTrigSeries gives a simpler result:
The two results are equivalent:
FourierCosSeries of a scaled TriangleWave:
Applications (2)
Properties & Relations (3)
Use FunctionExpand to expand TriangleWave in terms of elementary functions:
Use PiecewiseExpand to obtain piecewise representation on an interval:
TriangleWave[x] is both upper and lower semicontinuous, and thus continuous, at the origin:
This is different from SquareWave[x], which is only upper semicontinuous:
As well as SawtoothWave[x], which is only lower semicontinuous:
Possible Issues (1)
TriangleWave is undefined for complex numbers:
Related Guides
Related Links
History
Text
Wolfram Research (2008), TriangleWave, Wolfram Language function, https://reference.wolfram.com/language/ref/TriangleWave.html.
CMS
Wolfram Language. 2008. "TriangleWave." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TriangleWave.html.
APA
Wolfram Language. (2008). TriangleWave. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TriangleWave.html
BibTeX
@misc{reference.wolfram_2025_trianglewave, author="Wolfram Research", title="{TriangleWave}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/TriangleWave.html}", note=[Accessed: 16-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_trianglewave, organization={Wolfram Research}, title={TriangleWave}, year={2008}, url={https://reference.wolfram.com/language/ref/TriangleWave.html}, note=[Accessed: 16-January-2026]}