TuringMachine

TuringMachine[rule,init,t]

指定されたルールで初期条件 init から t ステップ進んだチューリングマシンの進化を表すリストを生成する．

TuringMachine[rule,init]

init を1ステップ進化させた結果を与える．

TuringMachine[rule]

進化の1ステップに相当するTuringMachineの演算子形である．

詳細

  • 一次元のチューリングマシンの場合，TuringMachineで生成された進化の各ステップは{{s,x,dx},{a1,a2,…}}の形で与えられる．ここで，頭部の状態は s であり，テープ上のセルは値 aiを持ち，頭部は aiと相対的な位置 x にあり，初期位置と比べて dx 動いている．
  • dx がチューリングマシンの初期条件から省略された場合，dx は0とみなされる．
  • d 次元のチューリングマシンでは，テープは d 次元の配列で指定され，位置 x と相対的位置 dx は長さ d のリストになる．
  • チューリングマシンのルールは{si,ai}->{spi,api,offi}の形の置換のリストで与えられる．その要素は次のようになる．
  • si頭部の状態
    ai頭部の下のセルの値
    spi頭部の新しい状態
    api頭部の下のセルの新しい値
    offi頭部が動くオフセット
  • 状態とセルの値は整数，パターン，任意の式のいずれでもよい．個々のセルの値はリストにはできない．
  • 一次元では，各オフセット offiは1個の整数である．次元が高くなると整数のリストになる．
  • 状態とセルの値が，それぞれ1から 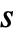s までと0から 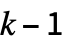k-1までの範囲の整数であるとされる場合，rule として次の形を与えることができる．
  • n数 n の状態が2つで色も2色のマシン
    {n,s}数 n の状態が s 個で色が2色のマシン
    {n,s,k}数 n の状態が s 個で色が k 色のマシン
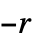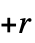    {n,s,k,r}-r から+r の範囲（0を除く）で offiを許容する
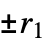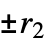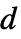    {n,s,k,{r1,r2,…,rd}}オフセット+/-r_(1), +/-r_(2), …の d 次元マシン
    {n,s,k,{{off1},{off2},…}}指定された明示的オフセットを許容するマシン
    {rule,s,k}明示的なルールを与えられたマシン
    rule明示的なルールを与えられたマシン（s と k は推測される）
  • 可能なチューリングマシンルールの数は次の通りである．
  • 2状態2色のマシン4096
    s 状態 k 色のマシン(2 s k)^(s k)
    s 状態 k 色で範囲 r のマシン(2 r s k)^(s k)
    二次元で s 状態 k 色のマシン(8 s k)^(s k)
  • マシンがそれ自身が置かれている構造についてのルールを持たない場合，その構造は変化しない．
  • TuringMachineは，与えられた構成に対してルールが複数の指定を持っている場合はリストの先頭の物を使う．
  • {rule,s,k}の形を使って，指定された構成に対してルールに必ずしも1つの例しかない訳ではない，多方向，非決定性，あるいはその他のチューリングマシンが指定できる．
  • 典型的な初期条件 init の形は次の通りである．
  • {s,{{},0}}頭部の状態 s，0で埋められた一次元テープ上
    {s,{{a1,a2,…},0}}無限テープ上の値 aiで区切られた範囲
    {{s,x},{{a1,a2,…},0}}頭部が最初は位置 xにある有限範囲
    {{s,…},{{a1,…},{b1,…}}}値 biの反復する背景
    {{s,…},{a1,a2,…}}有限テープ，循環を仮定
  • TuringMachine[rule,init,t]は，長さ 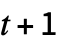t+1の進化リストを生成する．
  • TuringMachine[rule][init]はTuringMachine[rule,init]に等しい．

例題

すべて開くすべて閉じる

例  (5)

初期テープが4つの0からなり3ステップ進化する，2状態，2色のマシン2506：

無限の0のテープの4ステップ進化する，2状態，2色のマシン2506：

テープの連続する形状をプロットする：

チューリングマシンのルールアイコンを表示する：

ヘッドの状態も含め，進化をプロットする：

明示的な遷移で指定されたチューリングマシンのルールアイコンを示す：

頭部の状態も含めて進化をプロットする：

パターンに基づく遷移規則で指定されたチューリングマシン：

スコープ  (17)

一次元ルール  (6)

2状態1色のマシン2506：

進化をプロットする：

ヘッドの状態も含め，進化をプロットする：

3状態2色のマシン2139050：

ルールアイコンを生成する：

範囲が2で2状態2色のマシン16220：

ジャンプのオフセットがと2の，3状態2色のマシン2139050：

明示的な遷移規則を与える：

同じ遷移規則に対して状態数 s と色数 k の値を明示的に指定する：

初期条件  (9)

ヘッドの指定  (4)

ヘッドの状態が1から始まる，2状態2色のマシン2506：

進化：

ヘッドの状態が2から始まる，2状態2色のマシン2506：

進化：

初期テープでヘッドを位置3に置く：

初期テープでヘッドを位置5に置く：

テープの指定  (5)

循環を仮定して，4個の0を持つ有限テープで始める：

最も左のセルの左近傍は最も右のセルであり，逆もまた真である：

0の無限テープで始める：

無限に0がある背景上の1のテープで始める：

0の背景上のブロック211からなるテープで始める：

繰り返される02ブロックの背景上のブロック211で始める：

多次元ルール  (2)

2Dの2状態2色のチューリングマシン977401：

明示的な遷移で指定された二次元チューリングマシン：

アプリケーション  (12)

無限の0のテープからのWolframの単純なユニバーサルチューリングマシンの進化：

明示的な規則を使った別の形式：

2状態2色マシンの連続する進化を示す：

連続する初期条件からのマシンのヘッドの軌跡：

二次元マシンのヘッドでトレースされた進路：

多くのステップを経る二次元マシンのテープを平均する：

連続する初期条件からの連続する状態列：

連続する初期条件の一連の右または左への動き：

片側テープ上で停止する：

片側テープ上で関数を計算する：

ヘッドが新たなセルに達するステップだけを示す：

ヘッドが初期位置に戻るステップだけを示す：

ランダムな初期テープによる因果ネットワーク：

特性と関係  (4)

{n,s,k,…}の形式の規則のときは，ヘッドの状態とセルの値は，それぞれ1から s と0から k-1の整数でよい：

{n,s,k,…}の形式の規則のときは，0から k-1までの範囲外の値を持つセルにヘッドが到達するとマシンの進化が停止する：

進化が停止する別のチューリングマシン：

明示的な規則の集合を使って停止する状態を定義する：

進化をプロットする：

チューリングマシンの進化を生成する：

状態情報をテープの表現に「注入」する：

ヘッドの位置を赤い四角で示す：

RulePlotを使って完全な進化の図を生成する：

Wolfram Research (2007), TuringMachine, Wolfram言語関数， https://reference.wolfram.com/language/ref/TuringMachine.html （2021年に更新）.

テキスト

Wolfram Research (2007), TuringMachine, Wolfram言語関数， https://reference.wolfram.com/language/ref/TuringMachine.html （2021年に更新）.

CMS

Wolfram Language. 2007. "TuringMachine." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/TuringMachine.html.

APA

Wolfram Language. (2007). TuringMachine. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TuringMachine.html

BibTeX

@misc{reference.wolfram_2024_turingmachine, author="Wolfram Research", title="{TuringMachine}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/TuringMachine.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_turingmachine, organization={Wolfram Research}, title={TuringMachine}, year={2021}, url={https://reference.wolfram.com/language/ref/TuringMachine.html}, note=[Accessed: 17-November-2024 ]}