TuringMachine

TuringMachine[rule,init,t]

产生一个列表，表示按指定规则运行的图灵机从初始条件 init 开始，演化 t 步的过程.

TuringMachine[rule,init]

给出将初始条件 init 向前演化一步所得的结果.

TuringMachine[rule]

是 TuringMachine 的运算符形式，相当于向前演化一步.

更多信息

  • 对于一维图灵机 (Turing machine)，TuringMachine 演化的每一步由 {{s,x,dx},{a1,a2,…}} 的形式给出，当读写头处于状态 s 时，带中的格子具有值 ai，读写头的位置在相对于 ai 的 x 处，并相对于它的初始位置已经移动了 dx.
  • 如果图灵机的初始条件中省略了 dx，则会将其视为 0.
  • 对一个 d 维图灵机，带被指定为一个 d 维的数组，并且位置 x 和相对位置 dx 是长度为 d 的列表.
  • 一个图灵机的规则设定可以通过形式为 {si,ai}->{spi,api,offi} 的列表给出，其中的元素为:
  • si读写头的状态
    ai读写头下面格子的值
    spi读写头的新状态
    api读写头下面格子的新值
    offi读写头的偏移
  • 状态和格子的值可以是整数、模式，或其他表达式. 单个格子的值不能是列表.
  • 在一维情况下，每个位移 offi 是一个单一整数；在多维情况下，它是一个整数列表.
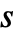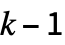  • 当状态和格子的值分别设置为1 到 s 及0到 k-1 范围内的整数时，rule 的替代形式如下所示：
  • n2 态 2 色带有数字 n 的机器
    {n,s}s 状态，2 色带有数字 n 的机器
    {n,s,k}s状态，k 色带有数字 n 的机器
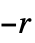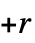    {n,s,k,r}允许位移 offi 在范围 -r 到 +r （不包括 0）
    {n,s,k,{r1,r2,…,rd}}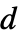d 维机器，带有 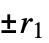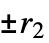+/-r_(1)，+/-r_(2), … 的偏移
    {n,s,k,{{off1},{off2},…}}允许指定位移的机器
    {rule,s,k}带有明确给定规则的机器
    rule给出显式规则（且 s、k 为推断）的机器
  • 可能的图灵机规则的数量为：
  • 2 态 2 色机器4096
    s 态 k 色机器(2 s k)^(s k)
    s 态 k 色范围 r 的机器(2 r s k)^(s k)
    二维 s 态 k 色机器(8 s k)^(s k)
  • 如果机器本身的格局中没有设置任何规则，则它的格局不会发生改变.
  • 如果规则对给定配置有多个规范，TuringMachine 将使用列出的第一个规范.
  • 形式 {rule,s,k} 可用于指定多路图灵机、非确定性图灵机和对于给定配置的规则不一定只有一种情况的其他图灵机.
  • 起始条件 init 的典型形式为:
  • {s,{{},0}}读写头处于状态 s，在一个全部为 0 的一维带上
    {s,{{a1,a2,…},0}}在一个无限带上的限制在 ai 的值的区域
    {{s,x},{{a1,a2,…},0}}开始时读写头处于位置 x 的有限区域
    {{s,…},{{a1,…},{b1,…}}}值 bi 的重复背景
    {{s,…},{a1,a2,…}}假定循环的有限带
  • TuringMachine[rule,init,t] 生成一个长度为 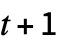t+1 的演化列表.
  • TuringMachine[rule][init] 等价于 TuringMachine[rule,init].

范例

打开所有单元关闭所有单元

基本范例  (5)

初始带 4 个 0 的 2 状态，双色机器 2506，演变为 3 个步骤：

0 的无限带的 2 状态，双色机器 2506，演变为 4 个步骤：

绘制带的连续格局：

显示图灵机的规则图标：

绘制演化，包括标头状态：

显示由显式转换指定的图灵机的规则图标：

绘制演化图，包括头部的状态：

由基于模式的转换规则指定的图灵机：

范围  (17)

一维规则  (6)

两态，两色机器 2506：

绘制演化：

绘制演化，包括标头的状态：

三态，两色机器 2139050：

产生规则图标：

2 态 2 色机器 16220，范围为 2：

三态，两色机器 2139050，跳跃补偿 和 2：

给出明确的过渡规则：

显式指定相同转换规则的状态数 s 和颜色数 k 的值：

初始条件  (9)

标头规范  (4)

两态，两色机器 2506，标头初始化在状态 1：

演化：

两态，两色机器 2506，标头初始化在状态 2：

演化：

包标头放在初始带的位置 3：

把标头放在初始带的位置 5：

带规范  (5)

开始于 4 个 0 的有限带，假设循环的：

最左原胞的左邻是最右原胞，反之亦然：

开始于 0 的无穷带：

开始于 0 的无限背景的 1 带：

开始于包含 0 的背景上的块 211 的带：

开始于重复的 02 块的背景上的块 211：

多维规则  (2)

2D 两态，两色图灵机器 977401：

由明确过渡指定的 2D 图灵机：

应用  (12)

来自于 0 的无限带的 Wolfram 最简单图灵机的演化：

使用明确规则的其他格式：

显示两态，两色机器序列的演化：

来自于连续初始条件的机器标头的轨迹：

由 2D 机器标头追踪的路径：

许多阶上 2D 机器的平均带：

来自于连续初始条件的连续状态序列：

连续初始条件的左或右移动序列：

停在单边带上：

单边带上的计算函数：

只显示标头达到新原胞的步骤：

只显示标头返回其初始位置的步骤：

来自于随机初始带的随意网络：

属性和关系  (4)

对于格式为 {n,s,k,…} 的规则，标头状态和原胞值可以分别为范围 1 到 s 和 0 到 k-1 的整数：

对于格式为 {n,s,k,…} 的规则，如果标头到达原胞的值不在范围 0 到 k-1，机器演化会停止：

其他演化停止的图灵机：

使用规则的明确集合定义停止状态：

绘制演化：

产生图灵机演化：

把状态信息“注入”带的表示：

用红方块显示标头的位置：

使用 RulePlot 产生完整的演化图：

Wolfram Research (2007)，TuringMachine，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TuringMachine.html （更新于 2021 年）.

文本

Wolfram Research (2007)，TuringMachine，Wolfram 语言函数，https://reference.wolfram.com/language/ref/TuringMachine.html （更新于 2021 年）.

CMS

Wolfram 语言. 2007. "TuringMachine." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/TuringMachine.html.

APA

Wolfram 语言. (2007). TuringMachine. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TuringMachine.html 年

BibTeX

@misc{reference.wolfram_2024_turingmachine, author="Wolfram Research", title="{TuringMachine}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/TuringMachine.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_turingmachine, organization={Wolfram Research}, title={TuringMachine}, year={2021}, url={https://reference.wolfram.com/language/ref/TuringMachine.html}, note=[Accessed: 17-November-2024 ]}