"HashSet" (データ構造)

"HashSet"

メンバが一般式であり，ハッシュ関数を使ってメンバシップが計算される集合を表す．

詳細

  • ハッシュ集合は，効率的な挿入と削除だけでなく，メンバシップの検証にも役立つ．
  • CreateDataStructure["HashSet"]新しい空の"HashSet"を作成する
    CreateDataStructure["HashSet",elems]elems を含む新しい"HashSet"を作成する
    Typed[x,"HashSet"]x に"HashSet"型を与える
  • "HashSet"型のデータ構造には，以下の演算が使える．
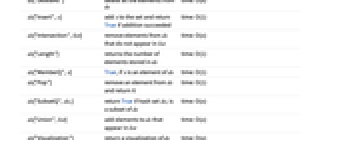
  • ds["Complement",list]list に現れる要素を ds から削除するtime: O(n)
    ds["Copy"]ds のコピーを返すtime: O(n)
    ds["Delete",x]x を ds から削除し，x が実際に要素である場合にTrueを返すtime: O(1)
    ds["DeleteAll"]ds からすべての要素を削除するtime: O(n)
    ds["Elements"]ds の要素のリストを返すtime: O(n)
    ds["EmptyQ"]ds が要素を持たない場合はTruetime: O(1)
    ds["Insert",x]x を集合に加え，追加に成功した場合にはTrueを返すtime: O(1)
    ds["Intersection",list]list に現れない要素を ds から削除するtime: O(n)
    ds["Length"]ds に保存される要素の数を返すtime: O(1)
    ds["MemberQ",x] x が ds のメンバである場合はTruetime: O(1)
    ds["Pop"]ds から要素を削除し，それを返すtime: O(1)
    ds["SubsetQ",ds1]ハッシュ集合 ds1が ds の部分集合である場合にはTrueを返すtime: O(n)
    ds["Union",list]list に現れる要素を ds に加えるtime: O(n)
    ds["Visualization"]ds の可視化を返すtime: O(n)
  • 以下の関数もサポートする．
  • dsi===dsjdsi が dsj に等しい場合はTrue
    FullForm[ds]ds の完全形
    Information[ds]ds についての情報
    InputForm[ds]ds の入力形
    Normal[ds]ds を通常の式に変換する

例題

すべて開くすべて閉じる

例  (2)

新しい"HashSet"は，CreateDataStructureを使って作成できる：

集合に挿入する：

集合には要素が1つ含まれる：

式が保存されているかどうかを検証する：

式が保存されていない場合には，Falseが返される：

要素を集合から削除する．何かが実際に削除された場合には，Trueを返す：

式バージョンの ds を返す：

要素は素早く挿入できる：

データ構造の可視化を生成することができる：

スコープ  (2)

情報  (1)

新しい"HashSet"は，CreateDataStructureを使って作成することができる：

データ構造 ds についての情報：

集合の演算  (1)

"HashSet"は，中心的な集合の演算のいくつかをサポートする．新しい空の"HashSet"は，CreateDataStructureを使って作成することができる：

要素を ds に挿入する：

"Union"の演算は，もともとデータ構造になかった要素を加える：

"Complement"の演算は，データ構造から要素を削除する：

"Intersection"の演算は，共通要素をデータ構造に残す：

アプリケーション  (1)

文字列集合  (1)

組込みの集合の演算は，機械数字の矩形配列を使う場合に便利である．データ構造の演算は，文字列等の数字ではないデータの集合に役立つ．1000000個の文字列のリストを作成する：

"Complement"が役に立つことを示す同様の例：

おもしろい例題  (1)

最大公約数の計算  (1)

2つの約数集合の共通集合を求めると，最大のものが求めやすくなる：

最大の結果は3である：

これは最大公約数に等しい：