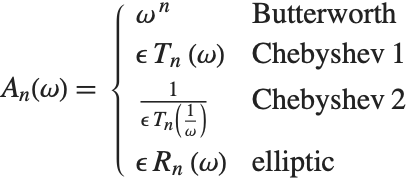アナログフィルタ設計

アナログフィルタ変換関数出力応答
アナログフィルタの極と零点異なるタイプのアナログフィルタ
アナログフィルタの周波数応答
Wolfram言語はアナログフィルタを設計するための包括的な方法をいくつも提供している．
アナログフィルタ変換関数
BiquadraticFilterModel
双二次フィルタモデル
ButterworthFilterModel
バターワースフィルタモデル
Chebyshev1FilterModel
第一種チェビシェフフィルタモデル
Chebyshev2FilterModel
第二種チェビシェフフィルタモデル
EllipticFilterModel
楕円フィルタモデル
BesselFilterModel
ベッセルフィルタモデル
アナログフィルタ設計方法
古典的フィルタはどれも特定の関数 により定義されている．ここで はフィルタの次数を定義する．
ここで は次数 の第一種チェビシェフ多項式であり， はチェビシェフ有理関数である． ベッセルフィルタは有理多項式で定式化された人気の高いアナログフィルタである．.
TransferFunctionModel
アナログフィルタの伝達関数
TransferFunctionExpand
展開された伝達関数
TransferFunctionFactor
因数分解された伝達関数
アナログフィルタの表現
以下は，カットオフ周波数が の二次バターワースフィルタモデルである：
次数5のバーターワースフィルタの伝達関数の大きさをプロットする：
指定された次数のローパスアナログフィルタの伝達関数である：
指定された次数のローパスアナログフィルタの伝達関数の大きさをプロットする：
アナログフィルタの極と零点
TransferFunctionPoles
アナログフィルタの極を抽出する
TransferFunctionZeros
アナログフィルタの零点を抽出する
アナログフィルタの極と零点
バターワースフィルタの極を表示する：
楕円フィルタの極と零点：
アナログフィルタの周波数応答
二次バターワースフィルタの周波数応答の平方：
周波数応答の平方の大きさをプロットする：
フィルタのボード線図：
指定された次数のローパスアナログフィルタのボード線図：
出力応答
バターワースフィルタの記号的ステップ応答：
数値的に計算されたフィルタのステップ応答：
ステップ応答をプロットする：
周波数の関数としての，バターワースフィルタの正弦波応答：
高周波正弦波をフィルタで除去する：
低周波正弦波をフィルタで除去する：
異なるタイプのアナログフィルタ

異なるタイプのフィルタを作成する

通過域端周波数が500ヘルツで減衰が1dB，阻止域端周波数が1000ヘルツで減衰が20dBのローパスバターワースフィルタを作成する：
通過域端周波数が500ヘルツで減衰が1dB，阻止域端周波数が1000ヘルツで減衰が20dBのハイパスバターワースフィルタを作成する：
通過域端周波数が500ヘルツで減衰が1dB，阻止域端周波数が1000ヘルツで減衰が20dBのバンドパスバターワースフィルタを作成する：
通過域端周波数が500ヘルツで減衰が1dB，阻止域端周波数が1500ヘルツで減衰が20dBのバンドストップバターワースフィルタを作成する：

フィルタタイプ間の変換

TransferFunctionTransform
変換関数を変換する
異なるフィルタタイプ間の変換
ローパスのアナログプロトタイプをハイパス，バンドパス，バンドストップに変換する：