Introduction to Constrained Optimization in the Wolfram Language
Optimization Problems
Constrained optimization problems are problems for which a function ![]() is to be minimized or maximized subject to constraints
is to be minimized or maximized subject to constraints ![]() . Here
. Here ![]() is called the objective function and
is called the objective function and ![]() is a Boolean-valued formula. In the Wolfram Language the constraints
is a Boolean-valued formula. In the Wolfram Language the constraints ![]() can be an arbitrary Boolean combination of equations
can be an arbitrary Boolean combination of equations ![]() , weak inequalities
, weak inequalities ![]() , strict inequalities
, strict inequalities ![]() , and
, and ![]() statements. The following notation will be used.
statements. The following notation will be used.
stands for "minimize ![]() subject to constraints
subject to constraints ![]() ", and
", and
stands for "maximize ![]() subject to constraints
subject to constraints ![]() ".
".
You say a point ![]() satisfies the constraints
satisfies the constraints ![]() if
if ![]() is true.
is true.
The following describes constrained optimization problems more precisely, restricting the discussion to minimization problems for brevity.
Global Optimization
A point ![]() is said to be a global minimum of
is said to be a global minimum of ![]() subject to constraints
subject to constraints ![]() if
if ![]() satisfies the constraints and for any point
satisfies the constraints and for any point ![]() that satisfies the constraints,
that satisfies the constraints, ![]() .
.
A value ![]() is said to be the global minimum value of
is said to be the global minimum value of ![]() subject to constraints
subject to constraints ![]() if for any point
if for any point ![]() that satisfies the constraints,
that satisfies the constraints, ![]() .
.
The global minimum value ![]() exists for any
exists for any ![]() and
and ![]() . The global minimum value
. The global minimum value ![]() is attained if there exists a point
is attained if there exists a point ![]() such that
such that ![]() is true and
is true and ![]() . Such a point
. Such a point ![]() is necessarily a global minimum.
is necessarily a global minimum.
If ![]() is a continuous function and the set of points satisfying the constraints
is a continuous function and the set of points satisfying the constraints ![]() is compact (closed and bounded) and nonempty, then a global minimum exists. Otherwise a global minimum may or may not exist.
is compact (closed and bounded) and nonempty, then a global minimum exists. Otherwise a global minimum may or may not exist.
Local Optimization
A point ![]() is said to be a local minimum of
is said to be a local minimum of ![]() subject to constraints
subject to constraints ![]() if
if ![]() satisfies the constraints and, for some
satisfies the constraints and, for some ![]() , if
, if ![]() satisfies
satisfies ![]() , then
, then ![]() .
.
A local minimum may not be a global minimum. A global minimum is always a local minimum.
Solving Optimization Problems
The methods used to solve local and global optimization problems depend on specific problem types. Optimization problems can be categorized according to several criteria. Depending on the type of functions involved there are linear and nonlinear (polynomial, algebraic, transcendental, ...) optimization problems. If the constraints involve ![]() , you have integer and mixed integer-real optimization problems. Additionally, optimization algorithms can be divided into numeric and symbolic (exact) algorithms.
, you have integer and mixed integer-real optimization problems. Additionally, optimization algorithms can be divided into numeric and symbolic (exact) algorithms.
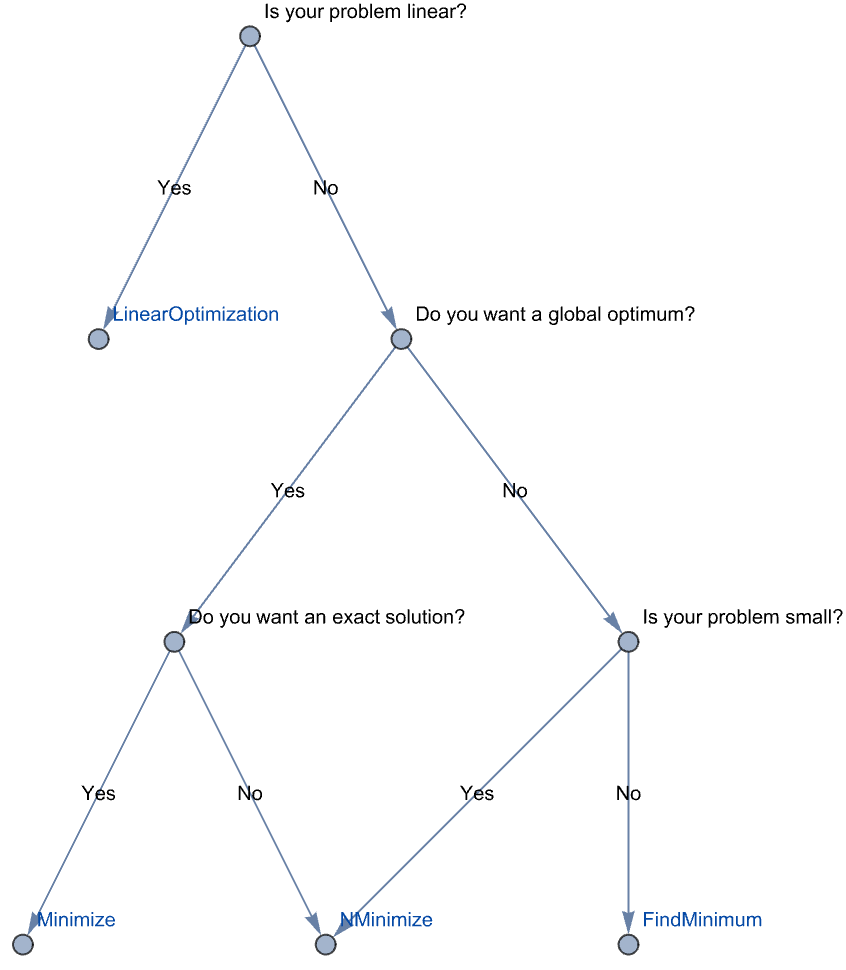
Wolfram Language functions for constrained optimization include Minimize, Maximize, NMinimize, and NMaximize for global constrained optimization, FindMinimum for local constrained optimization, and LinearOptimization for efficient and direct access to linear optimization methods. The following table briefly summarizes each of the functions.
Function | Solves | Algorithms |
| FindMinimum,FindMaximum | numeric local optimization | linear programming methods, nonlinear interior point algorithms, utilize second derivatives |
| NMinimize,NMaximize | numeric global optimization | linear programming methods, Nelder-Mead, differential evolution, simulated annealing, random search |
| Minimize,Maximize | exact global optimization | linear programming methods, cylindrical algebraic decomposition, Lagrange multipliers and other analytic methods, integer linear programming |
| LinearOptimization | linear optimization | linear optimization methods (simplex, revised simplex, interior point) |
Summary of constrained optimization functions.
Here is a decision tree to help in deciding which optimization function to use.