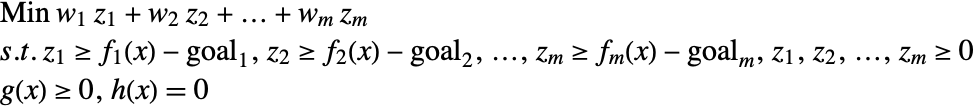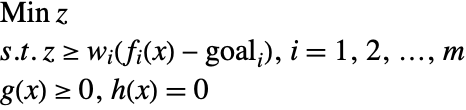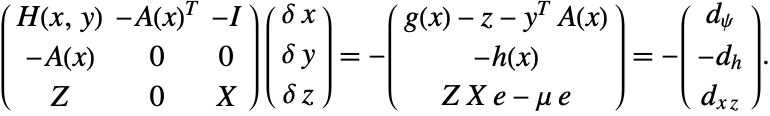Numerical Nonlinear Local Optimization

IntroductionExamples of FindMinimum
The FindMinimum FunctionNumerical Algorithms for Constrained Local Optimization

Introduction

Numerical algorithms for constrained nonlinear optimization can be broadly categorized into gradient-based methods and direct search methods. Gradient search methods use first derivatives (gradients) or second derivatives (Hessians) information. Examples are the sequential quadratic programming (SQP) method, the augmented Lagrangian method, and the (nonlinear) interior point method. Direct search methods do not use derivative information. Examples are Nelder–Mead, genetic algorithm and differential evolution, and simulated annealing. Direct search methods tend to converge more slowly, but can be more tolerant to the presence of noise in the function and constraints.

Typically, algorithms only build up a local model of the problems. Furthermore, to ensure convergence of the iterative process, many such algorithms insist on a certain decrease of the objective function or of a merit function that is a combination of the objective and constraints. Such algorithms will, if convergent, only find the local optimum, and are called local optimization algorithms. In the Wolfram Language local optimization problems can be solved using FindMinimum.

Global optimization algorithms, on the other hand, attempt to find the global optimum, typically by allowing decrease as well as increase of the objective/merit function. Such algorithms are usually computationally more expensive. Global optimization problems can be solved exactly using Minimize or numerically using NMinimize.

This solves a nonlinear programming problem, using Minimize, which gives an exact solution:
This solves the same problem numerically. NMinimize returns a machine-number solution:
FindMinimum numerically finds a local minimum. In this example the local minimum found is also a global minimum:

The FindMinimum Function

FindMinimum solves local unconstrained and constrained optimization problems. This document only covers the constrained optimization case. See "Unconstrained Optimization" for details of FindMinimum for unconstrained optimization.

This solves a nonlinear programming problem, using FindMinimum:
This provides FindMinimum with a starting value of 2 for x, but uses the default starting point for y:

The previous solution point is actually a local minimum. FindMinimum only attempts to find a local minimum.

This contour plot of the feasible region illustrates the local and global minima:
This is a 3D visualization of the function in its feasible region:

Options for FindMinimum

FindMinimum accepts these options.

option name
default value
AccuracyGoalAutomaticthe accuracy sought
CompiledAutomaticwhether the function and constraints should automatically be compiled
EvaluationMonitorNoneexpression to evaluate whenever f is evaluated
GradientAutomaticthe list of gradient functions {D[f,x],D[f,y],…}
MaxIterationsAutomaticmaximum number of iterations to use
MethodAutomaticmethod to use
PrecisionGoalAutomaticthe precision sought
StepMonitorNoneexpression to evaluate whenever a step is taken
WorkingPrecisionMachinePrecisionthe precision used in internal computations

Options of the FindMinimum function.

The Method option specifies the method to use to solve the optimization problem. Currently, the only method available for constrained optimization is the interior point algorithm.

This specifies that the interior point method should be used:

MaxIterations specifies the maximum number of iterations that should be used. When machine precision is used for constrained optimization, the default MaxIterations->500 is used.

When StepMonitor is specified, it is evaluated once every iterative step in the interior point algorithm. On the other hand, EvaluationMonitor, when specified, is evaluated every time a function or an equality or inequality constraint is evaluated.

This demonstrates that 10 iterations are not sufficient to solve the following problem to the default tolerance. It collects points visited through the use of StepMonitor:
The points visited are shown using ContourPlot. The starting point is blue, the rest yellow:

WorkingPrecision->prec specifies that all the calculation in FindMinimum is to be carried out at precision prec. By default, prec=MachinePrecision. If prec>MachinePrecision, a fixed precision of prec is used through the computation.

AccuracyGoal and PrecisionGoal options are used in the following way. By default, AccuracyGoal->Automatic, and is set to prec/3. By default, PrecisionGoal->Automatic and is set to -Infinity. AccuracyGoal->ga is the same as AccuracyGoal->{-Infinity,ga}.

Suppose AccuracyGoal->{a,ga} and PrecisionGoal->p, then FindMinimum attempts to drive the residual, which is a combination of the feasibility and the satisfaction of the Karush–Kuhn–Tucker (KKT) and complementary conditions, to be less than or equal to tol=10-ga. In addition, it requires the difference between the current and next iterative point, x and x+, to satisfy , before terminating.

This computes a solution using a WorkingPrecision of 100:
The exact optimal value is computed using Minimize, and compared with the result of FindMinimum:

Examples of FindMinimum

Finding a Global Minimum

If a global minimum is needed, NMinimize or Minimize should be used. However since each run of FindMinimum tends to be faster than NMinimize or Minimize, sometimes it may be more efficient to use FindMinimum, particularly for relatively large problems with a few local minima. FindMinimum attempts to find a local minimum, therefore it will terminate if a local minimum is found.

This shows a function with multiple minima within the feasible region of -10≤x≤10:
With the automatic starting point, FindMinimum converges to a local minimum:
If the user has some knowledge of the problem, a better starting point can be given to FindMinimum:
Alternatively, the user can tighten the constraints:
Finally, multiple starting points can be used and the best resulting minimum selected:
Multiple starting points can also be done more systematically via NMinimize, using the "RandomSearch" method with an interior point as the post-processor:

Solving Minimax Problems

The minimax (also known as minmax) problem is that of finding the minimum value of a function defined as the maximum of several functions, that is,

While this problem can often be solved using general constrained optimization technique, it is more reliably solved by reformulating the problem into one with smooth objective function. Specifically, the minimax problem can be converted into the following

and solved using either FindMinimum or NMinimize.

This defines a function FindMinMax:
This solves an unconstrained minimax problem with one variable:
This solves an unconstrained minimax problem with two variables:
This shows the contour of the objective function, and the optimal solution:
This solves a constrained minimax problem:
This shows the contour of the objective function within the feasible region, and the optimal solution:

Multiobjective Optimization: Goal Programming

Multiobjective programming involves minimizing several objective functions, subject to constraints. Since a solution that minimizes one function often does not minimize the others at the same time, there is usually no unique optimal solution.

Sometimes the decision maker has in mind a goal for each objective. In that case the so-called goal programming technique can be applied.

There are a number of variants of how to model a goal-programming problem. One variant is to order the objective functions based on priority, and seek to minimize the deviation of the most important objective function from its goal first, before attempting to minimize the deviations of the less important objective functions from their goals. This is called lexicographic or preemptive goal programming.

In the second variant, the weighted sum of the deviation is minimized. Specifically, the following constrained minimization problem is to be solved.

Here stands for the positive part of the real number . The weights reflect the relative importance, and normalize the deviation to take into account the relative scales and units. Possible values for the weights are the inverse of the goals to be attained. The previous problem can be reformulated to one that is easier to solve.

The third variant, Chebyshev goal programming, minimizes the maximum deviation, rather than the sum of the deviations. This balances the deviation of different objective functions. Specifically, the following constrained minimization problem is to be solved.

This can be reformulated as

This defines a function GoalProgrammingWeightedAverage that solves the goal programming model by minimizing the weighted sum of the deviation:
This defines a function GoalProgrammingChebyshev that solves the goal programming model by minimizing the maximum deviation:
This solves a goal programming problem with two objective functions and one constraint using GoalProgrammingWeightedAverage with unit weighting, resulting in deviations from the goal of 13.12 and 33.28, thus a total deviation of 37, and a maximal deviation of 33.28:
This solves a goal programming problem with two objective functions and one constraint using GoalProgrammingChebyshev with unit weighting, resulting in deviations from the goal of 16 and 32, thus a maximal deviation of 32, but a total deviation of 38:
This shows the contours for the first (blue) and second (red) objective functions, the feasible region (the black line), and the optimal solution found by GoalProgrammingWeightedAverage (yellow point) and by GoalProgrammingChebyshev (green point):

An Application Example: Portfolio Optimization

A powerful tool in managing investments is to spread the risk by investing in assets that have few or no correlations. For example, if asset A goes up 20% one year and is down 10% the next, asset B goes down 10% one year and is up 20% the next, and up years for A are down years for B, then holding both in equal amounts would result in a 10% increase every year, without any risk. In reality such assets are rarely available, but the concept remains a useful one.

In this example, the aim is to find the optimal asset allocation so as to minimize the risk, and achieve a preset level of return by investing in a spread of stocks, bonds, and gold.

Here are the historical returns of various assets between 1973 and 1994. For example, in 1973, S&P 500 lost 1-0.852=14.8%, while gold appreciated by 67.7%.

"3m Tbill""long Tbond""SP500""Wilt.5000""Corp. Bond""NASDQ""EAFE""Gold"
19731.075`0.942`0.852`0.815`0.698`1.023`0.851`1.677`
19741.084`1.02`0.735`0.716`0.662`1.002`0.768`1.722`
19751.061`1.056`1.371`1.385`1.318`0.123`1.354`0.76`
19761.052`1.175`1.236`1.266`1.28`1.156`1.025`0.96`
19771.055`1.002`0.926`0.974`1.093`1.03`1.181`1.2`
19781.077`0.982`1.064`1.093`1.146`1.012`1.326`1.295`
19791.109`0.978`1.184`1.256`1.307`1.023`1.048`2.212`
19801.127`0.947`1.323`1.337`1.367`1.031`1.226`1.296`
19811.156`1.003`0.949`0.963`0.99`1.073`0.977`0.688`
19821.117`1.465`1.215`1.187`1.213`1.311`0.981`1.084`
19831.092`0.985`1.224`1.235`1.217`1.08`1.237`0.872`
19841.103`1.159`1.061`1.03`0.903`1.15`1.074`0.825`
19851.08`1.366`1.316`1.326`1.333`1.213`1.562`1.006`
19861.063`1.309`1.186`1.161`1.086`1.156`1.694`1.216`
19871.061`0.925`1.052`1.023`0.959`1.023`1.246`1.244`
19881.071`1.086`1.165`1.179`1.165`1.076`1.283`0.861`
19891.087`1.212`1.316`1.292`1.204`1.142`1.105`0.977`
19901.08`1.054`0.968`0.938`0.83`1.083`0.766`0.922`
19911.057`1.193`1.304`1.342`1.594`1.161`1.121`0.958`
19921.036`1.079`1.076`1.09`1.174`1.076`0.878`0.926`
19931.031`1.217`1.1`1.113`1.162`1.11`1.326`1.146`
19941.045`0.889`1.012`0.999`0.968`0.965`1.078`0.99`
average1.0781.0931.1201.1241.1211.0461.1411.130

This is the annual return data:
Here are the expected returns over this 22-year period for the eight assets:
Here is the covariant matrix, which measures how the assets correlate to each other:
This finds the optimal asset allocation by minimizing the standard deviation of an allocation, subject to the constraints that the total allocation is 100% (Total[vars]==1), the expected return is over 12% (vars.ER≥1.12), and the variables must be non‐negative, thus each asset is allocated a non‐negative percentage (thus no shorting). The resulting optimal asset allocation suggests 15.5% in 3-month Treasury bills, 20.3% in gold, and the rest in stocks, with a resulting standard deviation of 0.0126:
This trades less return for smaller volatility by asking for an expected return of 10%. Now there is 55.5% in 3-month Treasury bills, 10.3% in gold, and the rest in stocks:

Limitations of the Interior Point Method

The implementation of the interior point method in FindMinimum requires first and second derivatives of the objective and constraints. Symbolic derivatives are first attempted, and if they fail, finite difference will be used to calculate the derivatives. If the function or constraints are not smooth, particularly if the first derivative at the optimal point is not continuous, the interior point method may experience difficulty in converging.

This shows that the interior point method has difficulty in minimizing this nonsmooth function:
This is somewhat similar to the difficulty experienced by an unconstrained Newton's method:

Numerical Algorithms for Constrained Local Optimization

The Interior Point Algorithm

The interior point algorithm solves a constrained optimization by combining constraints and the objective function through the use of the barrier function. Specifically, the general constrained optimization problem is first converted to the standard form

and . The non-negative constraints are then replaced by adding a barrier term to the objective function

where is a barrier parameter.

The necessary KKT condition (assuming, for example, that the gradient of is linearly independent) is

where is of dimension × and is a dual variable. The preceding can be written as:

where is a diagonal matrix, with the diagonal element of if , or and is a vector of 1s and . Introducing variable , the preceding system can be rewritten as:

and is a diagonal matrix with diagonal elements . This nonlinear system can be solved with Newton's method. Let and ; the Jacobi matrix of system (1) is

Eliminating , , then , thus

Thus the nonlinear constrained problem can be solved iteratively by

with the search direction given by solving the previous Jacobi system (2).

To ensure convergence, you need to have some measure of success. One way of doing this is to use a merit function, such as the following augmented Lagrangian merit function.

Augmented Lagrangian Merit Function

This defines an augmented Lagrangian merit function

Here is the barrier parameter and a penalty parameter. It can be proved that if the matrix is positive definite, then either the search direction given by (3) is a descent direction for the above merit function (4), or satisfied the KKT condition (5). A line search is performed along the search direction, with the initial step length chosen to be as close to 1 as possible, while maintaining the positive constraints. A backtracking procedure is then used until the Armijo condition is satisfied on the merit function, with .

Convergence Tolerance

The convergence criterion for the interior point algorithm is

with tol set, by default, to 10-MachinePrecision/3.