最適化問題

制約付き最適化問題とは，関数 が制約条件 に従って最大化あるいは最小化されるものである．は目的関数と呼ばれ，はブール値の式である．Wolfram言語では，制約条件は，式 ，弱い不等式 ，強い不等式 ， 宣言の任意のブール結合でよい．ここでは次の表記を使う．

は「制約条件に従って を最小化する」を表し，

は「制約条件に従って を最大化する」を表す．

が真であるなら，点 は制約条件を満足すると言う．

次では制約条件付き最適化問題をより明確に述べるが，簡潔にするため，ここでは最小化問題に限って論を進める．

大域的最適化

が制約条件を満たし，その制約条件を満たす任意の点 について であるなら，点 は制約条件を対象とする の「大域的最小点」と言う．

制約条件を満たす任意の点 について であれば，値 は制約条件 に従う の「大域的最小値」と言う．

大域的最小値 は，任意の とについて存在する．が真であり， であるような点 が存在するとき，大域的最小値 に「達した」と言う．そのような点 は必然的に極小値となる．

が連続関数で，制約条件を満たす点集合がコンパクト（閉じていて境界がある）であり，かつ空でない場合は，大域的最小点が存在する．その他の場合は，大域的最小点は存在する可能性もしない可能性もある．

局所的最適化

が制約条件を満たすとき点 は制約条件に従う の「極小値」と言う．また，の場合， がを満足するならば である．

極小値は大域的最小点とは異なることもある．大域的最小点は常に極小値である．

最適化問題を解く

局所的最適化問題および大域的最適化問題を解くのに使われるメソッドは，個々の問題のタイプによって異なる．最適化問題はいくつかの基準によって分類することができる．関係する関数のタイプによって，線形と非線形（多項式，代数的，超越...）の最適化問題に分けられる．制約条件が を含む場合は整数と整数-実数の混合した最適化問題になる．また，最適化のアルゴリズムは数値的アルゴリズムと記号的（厳密）アルゴリズムに分けられる．

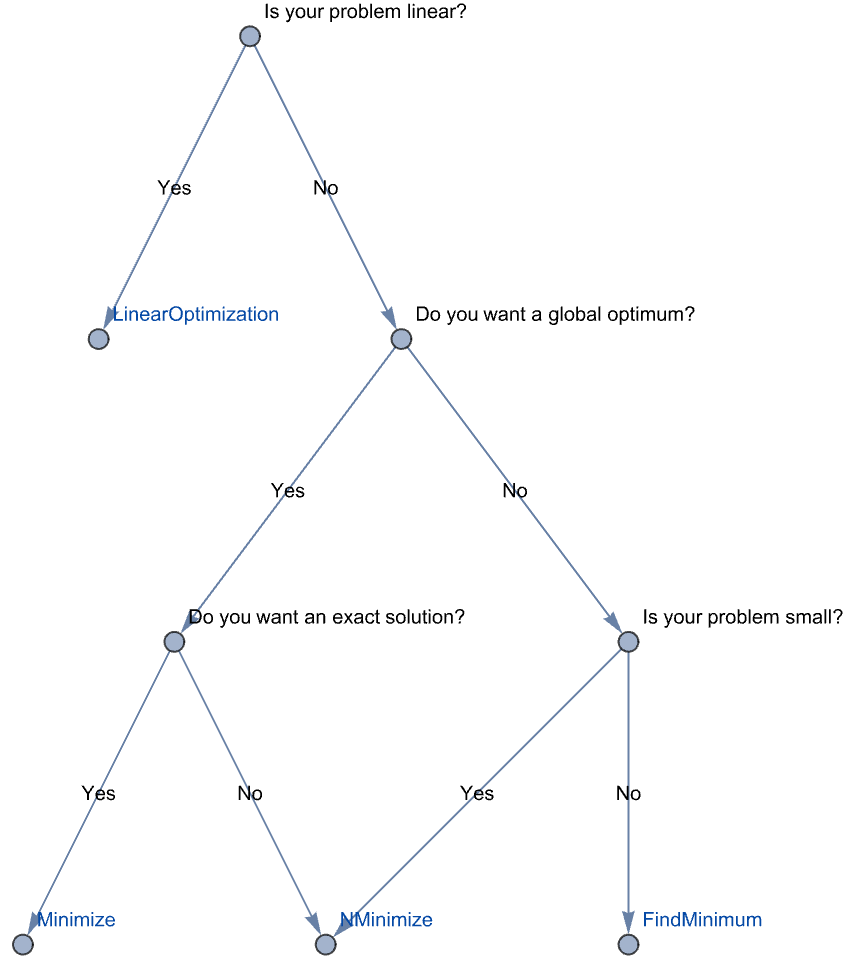
制約条件付き最適化のためのWolfram言語の関数には，大域的制約条件付き最適化にMinimize，Maximize，NMinimize，NMaximizeが，また局所的制約条件付き最適化にFindMinimumが，そして線形最適化メソッドに効率的に直接アクセスできるLinearOptimizationがある．次の表は各関数の簡単なまとめである．

制約条件付き最適化関数のまとめ

これは，どの最適化関数を使うかを決めるのに役立つ決定木である．

関連するテクニカルノート

▪
• 制約条件付き最適化
▪
• 線形最適化
▪
• 局所的非線形数値最適化
▪
• 大域的非線形数値最適化
▪
• 厳密な大域的最適化