Wolfram 语言中约束最优化介绍
最优化问题
约束最优化问题是在约束条件 
下最小化或最大化一个函数 
的一类问题. 这里 
称为目标函数， 而 
是一个布尔值的公式. 在 Wolfram 语言中约束条件 
可以是等式 
，弱不等式 
，严格不等式 
和 
语句的任意一个布尔组合. 我们将使用下面的符号表示.
下面我们对约束最优化问题进行更确切的描述，为简要起见，我们的讨论范围限制在最小化问题上.
全局最优化
我们说点 
是 
在约束条件 
下的一个全局最小值点，如果 
满足这些约束条件并且对于任意满足这些约束条件的点 
都有 
.
我们说值 
是 
在约束条件 
下的一个全局最小值，如果对于任意满足约束条件的点 
都有
.
全局最小值 
对于任意 
和 
都存在. 我们可以得到全局最小值 
，如果存在一个点 
满足 
的值为 true 并且
. 这样的一个点 
必然是全局最小值.
如果 
是一个连续函数并且满足约束条件 
的点集是紧緻的(闭集并且有界) 和非空的，那么一个全局最小值是存在的. 否则一个全局最小值可能存在也可能不存在.
局部最优化
我们说点 
是 
在约束条件 
下的一个局部最小值，如果 
满足约束条件，并且对于某 
，如果 
满足 
，那么 
.
一个局部最小值可能不是全局最小值. 一个全局最小值总是局部最小值.
求解最优化问题
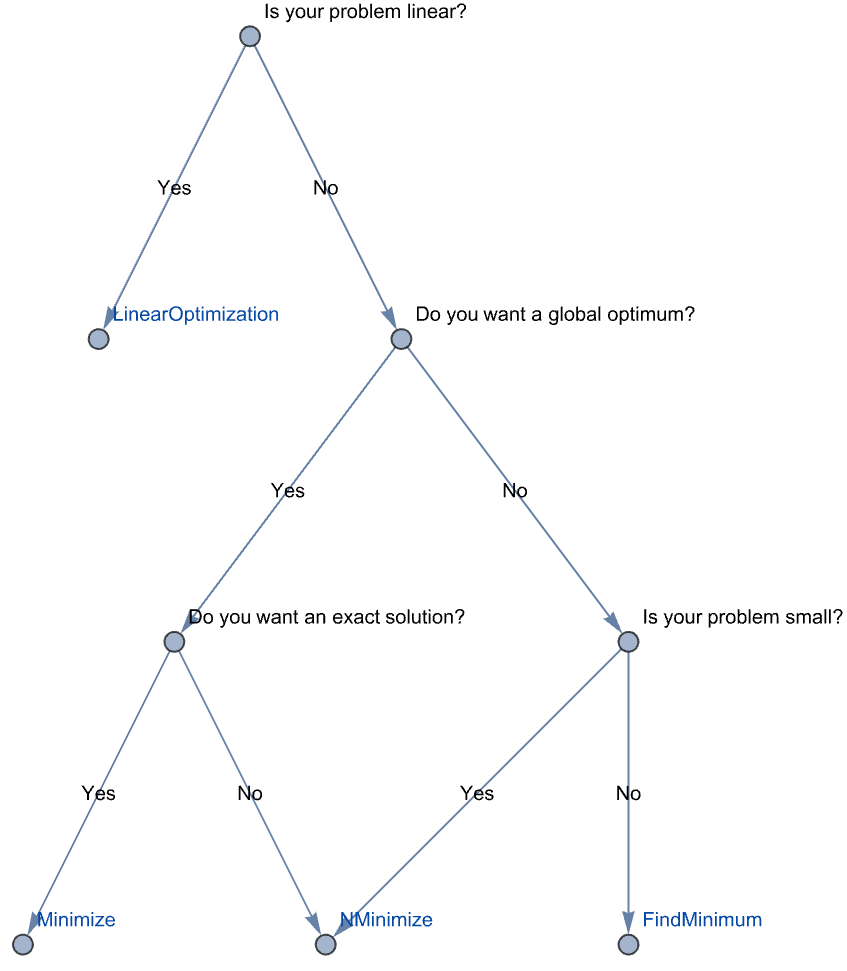
用以求解局部和全局最优化问题的方法取决于特定问题的类型. 最优化问题可以根据一些不同的标准分类. 根据所涉及到的函数类型，我们有线性和非线性 (多项式、代数、超越、 ...) 最优化问题. 如果约束条件涉及 
，我们就有了整数以及整数-实数混合最优化问题. 此外，最优化算法可分为数值和符号化 (精确) 算法.
关于约束最优化的 Wolfram 语言函数包括 Minimize、Maximize、关于全局约束最优化的NMinimize、NMaximize、关于局部约束最优化的 FindMinimum 和提供了对线性最优化方法有效直接应用的 LinearOptimization. 下面的表格对各个函数进行了简要的总结.
函数 | 求解 | 算法 |
| FindMinimum、FindMaximum | 数值局部最优化 | 线性规划方法、非线性内点算法、利用二阶导数 |
| NMinimize、NMaximize | 数值全局最优化 | 线性规划方法、Nelder-Mead、差分进化、模拟退火、随机搜索 |
| Minimize、Maximize | 精确全局最优化 | 线性规划方法、柱形代数分解、拉格朗日乘子法和其他分析方法、整数线性规划 |
| LinearOptimization | 线性最优化 | 线性最优化方法(单纯型法、修正单纯型法、内点法) |
