初始和边界值问题

初始 (IVP) 和边界值问题 (BVP) 综述非线性 IVP 和 BVP
线性 IVP 和 BVP带有分段系数的 IVP

初始 (IVP) 和边界值问题 (BVP) 综述

DSolve 可用于求解微分方程或微分方程组的通解. 通解提供有关问题的完整解空间结构的信息. 然而，在实践中，人们通常仅对满足与应用领域相关的某些条件的特定解感兴趣. 这些条件通常有两种类型.

  • 解 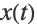和/或其导数要求在一个单点上有特定的值，例如， 和 . 这类问题传统上称为初值问题 (IVP)，因为假定系统从固定的初始点(本例中为0)开始演化.
  • 解 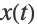需要在一对点上有特定的值，例如， 和 . 这些问题称为边值问题 (BVP)，因为点 0 和点 1 被视为应用中感兴趣领域的边界点(或边).

IVP 和 BVP 的符号解需要问题的通解知识. 最后一步，使用初始值或边界值获得特定解，主要涉及代数运算，并且对于 IVP 和 BVP 类似.

由于最终的代数步骤涉及线性方程的解，因此线性微分方程的 IVP 和 BVP 被相当容易地求解. 然而，如果基础方程是非线性的，那么解可以有几个分支，或者来自通解的任意常数可以出现在超越函数的不同参数中. 因此，并非总能完成非线性问题的最终代数步骤. 最后，如果基础方程具有分段（即，不连续）系数，则 IVP 在系数连续的区域上自然地分解为更简单的IVP.

线性 IVP 和 BVP

首先，考虑线性一阶 ODE 的初始值问题.

这是一个线性的一阶 ODE：
请注意，通解是任意常数 C[1] 的线性函数：
求初始条件 的特定解：
这验证了解满足方程和初始条件：
这是一般初始条件 的同一问题的解：
这绘制了不同 值的方程的几个积分曲线. 该图显示，如果参数 位于 和 之间，则解具有拐点，而对于 的其他值，则出现全局最大值或最小值：
这是一个线性二阶方程的解，在 时为 和 规定初始值：
这验证了解满足方程和初始条件：
以下是解的图：
获取问题解的更多信息，设置 ：
以下是不同初始方向的解的图. 根据 的值是否小于或大于 ，当 ，解逼近 或 ，这是 ODE 的辅助方程的最大根：
这是一个非齐次线性二阶方程的 BVP：

应当注意，与初始值问题相反，当规定边界值时，没有一般存在或唯一性定理，并且在某些情况下可能没有解.

这个问题没有解，因为通解中 C[2] 项在 和 都消失了. 因此，参数 C[1] 有两个不一致的条件并且解是一个空集：

先前对线性方程的讨论泛化了高阶线性 ODE 和 ODE 线性系统的情况.

以下是针对四阶线性 ODE 的初始值问题 (IVP) 的解：
验证解和初始条件：
由于这是一个四阶 ODE，因此必须指定四个独立条件才能找到 IVP 的特定解. 如果条件数量不足，DSolve 返回的解可能包含一些任意参数，如下所示：
最后，这是一个用于线性 ODE 系统的 IVP 解：
验证解是否满足系统和初始条件：
解 、 和 由变量 参数化，并且可以在平面中单独绘制或作为空间曲线绘制：

非线性 IVP 和 BVP

许多实际应用需要针对非线性 ODE 的 IVP 和 BVP 的解. 例如，考虑逻辑方程，它发生在人口动力学中.

这是逻辑方程：
方程的右边可以扩展为 y[t] 中的二次多项式. 因此，逻辑方程只是一个 Riccati 方程，可以很容易地找到它的通解：
这将内在增长率 r 设置为 1/2，将饱和度级别 K 设置为 4 并求解初始值问题：
这解决了具有符号参数 r 和 K 的逻辑方程的初值问题：
这验证了解满足方程和初始条件：
以下是 r 和 K 的不同值的解的图：
以下是二阶非线性 ODE 的 IVP 示例，其通解可以以显式形式获得：
这验证了解满足方程和初始条件：
最后，这是非线性二阶 ODE 的边值问题. 该解需要满足在 0 和无穷大处的边界条件. 在根据 JacobiSN（EllipticF 的逆）求通解的同时生成 Solve::ifun 消息. 给出 DSolve::bvlim 消息是因为无法为通用解的任一分支计算满足条件 y′[Infinity]0 所需的限制. 然而，边界值问题的解是使用其他方法来确定通解中的常量 C[1] 和 C[2] 的值：

对于非线性方程，可能无法始终获得 IVP 或 BVP 的符号解. 在这种情况下可能需要数值方法.

带有分段系数的 IVP

在现代应用中出现的微分方程通常具有不连续的系数. DSolve 可以使用分段系数处理各种这样的 ODE. 这些方程中使用的一些函数是 UnitStep、Max、Min、Sign 和 Abs. 这些函数及其组合可以转换为 Piecewise 对象.

这会将给定的表达式转换为 Piecewise 表达式：
以下是包含 UnitStep 的一阶 ODE 的通解：
以下是具有初始条件的相同 ODE 的解：
可以通常的方式绘制解. 请注意，解是连续的，但在 处不可微：
验证解：
这是一个分段 ODE，其系数中包含 Max：

分段 ODE 可以被认为是不相交间隔上的 ODE 的集合，使得系数和边界条件的表达式从一个区间变化到另一个区间. 因此，不同的区间具有不同的解，并且通过在不同的区间上将解拼接在一起来获得 ODE 的最终解.

对于这个分段 ODE，FinalSol 的表达式是通过将 SolFromMinusInfinityToTwo 和 SolFromTwoToInfinity 拼接在一起获得的. 区间 (-Infinity,2] 的边界条件只是 ，而区间 [2,Infinity) 的初始条件是 （由第一区间解的最终值给出）：

如果问题中存在大量不连续性，则在问题的公式化中直接使用 Piecewise 是很方便的.

这个二阶 ODE 包含一个 Piecewise 项：
该 ODE 包含 Clip 函数. 解以 Airy 函数形式给出：