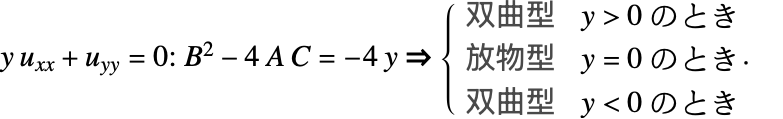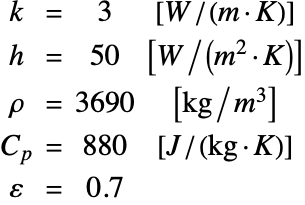はじめに

流体力学，電気学，電磁気学，機械学，古典光学，および熱流量における物理現象のほとんどは，偏微分方程式(PDE)で表される．実際，マクスウェル(Maxwell)方程式，ナビエ・ストークス(Navier–Stokes)方程式，熱方程式，波動方程式，量子力学におけるシュレディンガー(Schrödinger)方程式等の有名な物理法則はPDEで記述されている．つまりこれらの法則は物理現象を空間と時間の導関数を関連付けることによって表しているのである．これらの方程式の導関数は，速度，加速度，力，摩擦力，流速，電流のような数量を表す．このため，求めたい未知の数量の偏導関数に関連した方程式があるのである[1–3]．

PDEは多変数関数のさまざまな偏導関数を含む方程式である．未知の関数が1つの変数だけに依存する常微分方程式(ODE)とは異なり，PDEでは未知の関数はいつくかの変数に依存する．例えば，温度場 が場所 x と時間 t の両方に依存することもあり得る[2]．

このモノグラフでは，簡素化のために以下の偏導関数の表記を使うことにする：

この省略表記法を使って，単位係数を含む有名なPDE[3]をいくつか挙げる：

未知の関数 u は「従属変数」と呼ばれ，時間 t や，x 等の空間座標のようないくつかの「独立変数」の関数である．PDEは従属変数 u(x,t)が独立変数について微分される項から構築される．例えば，一次元熱方程式 では，従属変数 は2つの独立変数 x と t の関数であり，極座標のラプラス方程式 では，従属変数 は r と θ に依存している[4]．

PDEを満足する関数 はPDEの「解」と呼ばれ[5]，通常これは未知であるため求められる．

一般的な理論や解法は通常指定されたクラスの方程式にのみ当てはまるので，PDEの分類は重要である．PDEの基本的な分類は次のようにリストすることができる[6]．

1.   「PDEの階数」．PDEの「階数」とは，方程式の中に含まれる偏導関数の最高階数である．例えば，以下のようになる．

2.   「変数の数」．変数の数とは独立変数の数である．例えば，以下のようになる．

2つの独立変数を持つ最も一般的な一階偏微分方程式は，次のように書くことができる：

ここで はその引数の関数，つまり に含まれている導関数の最高階が1であることを表す．

同様に，2つの独立変数を持つ最も一般的な二階偏微分方程式は，次のように書くことができる：

3.   「係数の種類」．方程式( 7 )の係数 ， ， ， ， ， が定数ならば，( 8 )は定数係数偏微分方程式と呼ばれ，それ以外の場合は変数係数偏微分方程式と呼ばれる[ 9 ]．

4.  「線形性」．偏微分方程式は線形でも非線形でもあり得る．従属変数 u およびその偏導関数すべてがPDEで線形に現れたら，そのPDEは「線形」である．より正確に言えば，「独立変数が2つの二階線形偏微分方程式」は次の形式の方程式である．

ここで ， ， ， ， ， ， は定数である可能性もあれば，独立変数のみの指定された関数で ， ， すべてが同時にゼロではない可能性もある[ 10 ]．

この概念は重要であるため，もう少し例を挙げる．

一般に， が任意の関数 ， および任意の定数 について および を満足する微分演算子ならば， は「線形微分方程式」である．

上で与えられたPDE を考えたとき，以下の理由で は線形であると言える：

同様に，PDE の場合，以下の理由で は非線形であることが分かる：

微分演算子 の線形性の結果として生じる重要な特性は， と の両方が解であるなら， も解であるということである．これは「重ね合わせの原理」とも呼ばれる．

5.   「斉次性」．右辺 が恒等的にゼロならば，方程式( 11 )は斉次方程式と呼ばれる．それ以外の場合，つまり が恒等的にゼロではない場合は，その方程式は非斉次方程式と呼ばれる[ 12 ]． 線形性に起因する別のことに， が線形微分演算子であるとき， の解（斉次解）を の解に（非斉次解）足したら，非斉次解が得られるというものがある[ 13 ]．

このモノグラフでは，先の分類に従ってPDEを調べていく．まず最も簡単なPDEから始めて，徐々に難しいものへと移行する．各クラスについて，それらの問題を解くのに利用できるメソッドを見ていく．記号解法がまだ利用できないPDEについてはNDSolveを使うことをお勧めする．

m 階の線形斉次常微分方程式(ODE)の一般解は，m 個の独立解と m 個の任意定数の線形結合であることを思い出してほしい[14]．簡単なPDEを扱うときにこの点がどう変化するかを見てみよう．

最も簡単なPDEは （ここで ）である．その一般解は であり，は1変数の任意の関数である．例えば，，，， がいくつかの解である．解は に依存しないので，xy 平面の線分 （ は定数）上で一定である．

このPDEでは，DSolveは次を返す：

以下のManipulate は，解が の曲線上で一定であることを示している：

の解 が求めたいとする．PDEを x について1回積分すると，（は任意関数）が得られる. PDEには変数 x の他に変数 y も含んでいたため，積分定数は通常の定数係数ではなく になった．を x についてもう一度積分すると が得られる．この解には2つの任意関数があり，この関数は積分定数がODE内で行うのと同じ役割を果たす[15]．

DSolveはこのPDEに同等の結果を返す：

の解 が求めたいとする．実際のところ，y に関する微分法はなく，y はPDEに明示的に現れていないので，この方程式は追加の独立変数 y を持つODEである．と の代りに積分定数として任意関数 と を使うと，ODE の一般解は なので，PDEの解は である[16]．

このPDEにDSolveは同じ結果を返す：

の解 が求めたいとする．まず，y が固定されているものとして x についてPDEを積分すると，（は任意関数）が得られる．次に x が固定されているものとして y について を積分すると，解 が得られる．ここで および （ である）は任意関数である[17]．

DSolveはこのPDEに同じ結果を返す：

初期条件と境界条件

前の例で見たように，PDEは通常任意関数を含む解を持つ．特定の解を選び出すためには，追加の補助条件が必要になる．つまり，一意解を指定する条件を課すのである．これらの条件は問題の性質が動機となったものであり，初期条件および境界条件として課される[18]．

「初期条件」は正確な時間 における時間依存PDEの物理的状態を定義する．

例えば，拡散方程式では初期条件は以下になる．

ここで は空間変数を表すベクトル を持つ既知の関数である．拡散物質では は初期濃度であり，熱流では は初期温度である[19]．

波動方程式の場合，初期条件はペアで与えられる：

ここで は初期位置，は初期速度である．問題の物理特性から，後の時間において位置 を一意に決定するためには，これら両方が指定されていることが必須である[20]．

要約すると，PDEの時間導関数の各次で1つの初期条件が指定されなければならないのである．

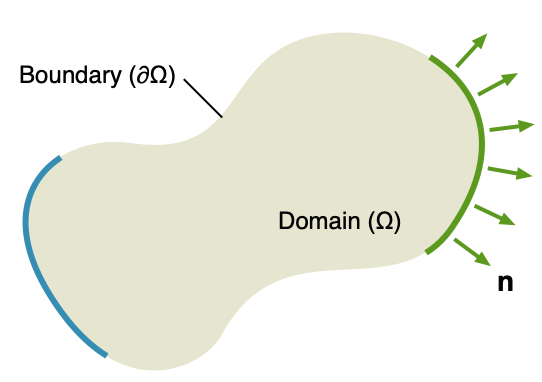
現実世界で使用するPDEは領域Ωで使用できるように限られている．例えば，長さ l の振動弦ではΩは区間 である．∂Ωで表されるΩの境界には および の2点のみが含まれる．太鼓の皮の場合，領域は平面でありその境界はその面を囲む閉じた曲線であるが，拡散する化学物質の場合はΩはその液体が入った容器なので ∂Ωはその境界面 である[21]．

「境界条件」は，領域Ωで使用できる偏微分方程式と，その領域外で解の一部ではないものとの接触部分である．一意解を求めるためにはいくつかの「境界条件」を指定することが必要である．境界条件の中で最も重要で一般的な3つのタイプは以下である：

1.   ディリクレ(Dirichlet)条件 ： が境界 ∂Ω 上で指定される．

2.  ノイマン(Neumann)条件：法線微分 が境界 ∂Ω上で指定される．

3.   ロビン(Robin)条件： が境界 ∂Ω 上で指定される．

これらの条件では a は x と t の関数であり，各条件はすべての t および境界 上のすべての x について成り立つものと想定される[22]．

システム関数のNeumannValueと，ここで使われているノイマン条件・ロビン条件の間には関連性はあるが，定義は異なることに注意する．

図1では，ディリクレ条件が指定できる場所は，領域Ωの境界 上に青で示してある．ディリクレ条件はこれらの点で満足される解の値を指定する．ノイマン条件が指定できる場所は領域Ω上の境界 上に緑で示してあり，これは境界 上の外向きの法線の方向の内向き流束を指定する．

通常，境界条件は方程式として書かれる．例えばノイマン条件は次の方程式で書かれる：

ここで g は与えられた関数である．これらの境界条件はどれも，指定された関数が ならば斉次という．それ以外の場合は非斉次と呼ばれる．図1で はΩから外向きを指す，∂Ω上の単位法線ベクトルを表し， は内向きの法線方向の u の方向導関数を表す[23]．

Ω が区間 に過ぎないという一次元問題では，境界は2つの端点からのみなり，その境界条件は以下の簡単な形式を取る：

ここで ，，，は t の関数であり得る．境界上の異なる場所で異なるタイプの境界条件を持つことができる[24]．

初期条件で指定される時間依存PDEは「初期値問題」，境界条件付きのPDEは「境界値問題」と呼ばれる．初期条件と境界条件の両方を持つ時間依存PDEは「初期値境界値問題」と呼ばれる．

（ここで，）で与えられた境界条件を持つ微分方程式 が解きたいとする．

先に，方程式 が一般解 を持つ例を見た．ここで与えられた境界条件 を使うと， が求まるため，この問題の解は であると一意に決まる．

この境界値問題では，DSolveは次を返す：

定数係数を持つ以下の問題が解きたいとする[25]：

ここで ， である．

この問題ではDSolveValueは以下を返す：

前述の問題を解いているとき，DSolveValueは通常「Fokas法」または「一様変換法」と言われる方法を使う．変数の分離と特定の積分変換に依存する，定数係数線形偏微分方程式の従来の解法とは異なり，Fokas変換法は特別な境界条件の特定の方程式に限られない．このメソッドの詳細はこのモノグラフの扱う範囲を超えるので，[26]をご参照いただきたい．

一階線形方程式—特性曲線法

2つの独立変数を持つ，一般的な一階線形偏微分方程式の初期値問題は以下で与えられる：

一階線形PDEの解法の一つに，特性曲線法がある．これは(27)より解きやすい常微分方程式の初期値問題を得るために，独立変数から新しい変数への変化を求めようとするものである[28]．

詳細に入る前に，この方法を解説するために，問題(29)の解を知っているとする．また，解 は滑らかで， ，であるような x-t 平面に滑らかなパラメトリック曲線（これを特性曲線という）があるとする．つまり， と は単独のパラメータ の関数である．ここでこれらのパラメトリック曲線を移動するにつれて解がどのように変化するかを考える：

上記の関係(30)と(31)のPDEの左辺との間の類似点を使っていることに注目する．

となるような および が求められるとすると，(32)のPDEは以下のようにODEに還元される：

したがって，，つまりパラメトリック曲線の最初の点が既知である場合，は一意に決まる．

ここで「問題(33)を常微分方程式の初期値問題に還元する特性曲線をどのように求めるか」という質問に答えなければならない．

特性曲線を求め，その結果のODE(34)を一意に解くためには，初期値問題を定義する必要がある．新しい座標 s（x と t をパラメータ化するためのもの）および τ（初期曲線のためのもの）は以下の特性を持たなければならない[35]：

1.   は初期曲線（この場合 ）から始まり，0から∞の範囲を特性曲線 に沿って変化する．

2.   は初期曲線 に沿って変化し，それぞれの特性曲線に沿って一定である．

以下の図は，これらの特性を表している[36]：

それゆえ，新しい変数 s と τ で特性曲線を一意に定義するために，初期値問題を定義する：

および

なので，のとき である．新しい座標系でははにマップされる．したがって初期条件 は，還元された s の常微分方程式(37)の初期条件として動作するよう に変換される．

連鎖法則と前述の特性を適用することによって，次の常微分方程式の初期値問題に辿り着く：

PDE問題(38)は特性曲線に沿って，常微分方程式の初期値問題(39)に還元される．新規に構築されたこの問題を解いたら，もとの独立変数に戻し，もとのPDE(40)の解を求める[41]．

要約すると，このアプローチは：

3.   新しい変数 が特性曲線 を定義し，その曲線のどれもが を初期点とする．初期データは曲線に沿って伝搬する．

4.   s 座標は特性曲線に沿った点を示す

5.   座標は与えられた曲線の初期点( )を表す

6.  PDEを特性曲線で表すことで得られたODEによると，各 について，初期値 は点から始まる曲線に沿って発展するというもので，「特性曲線法」と言われる．

(42)の特性方程式 , は自律である．「自律」という言葉は，方程式が s に明示的に従属していないときに使われる．

特性曲線はODEを満足する：

したがって，問題(43)について，特性曲線は解 u とは無関係に解くことができる．

次の例で示すように，方程式(44)はこのメソッドを適用するときに使われた基礎方程式である．

(45)において ならば，u は特性曲線上で一定である．

以下の定数係数方程式

を解いてみる．ここで a と b は定数であり両方とも非零である．y に t の役割をさせ(46)を使うと，特性曲線はODE を満足する．このODEを解くと以下が得られる：

は特性曲線である．前述の通り，はそれぞれの曲線上で一定である．したがって，（f は任意関数）となる．(47)の一般解は を について解くことで得られる：

つまり

となり，DSolveで直接同等の解が得られる：

上の解は簡単に検証できる：

次の方程式

は線形であり斉次であるが，変数係数(y)を持っている．これについて特性曲線はODE を満足する．このODEを解くと以下が得られる：

は特性曲線である．前述の通り，は各曲線上の定数である．ゆえに （f は任意関数）である．(48)の一般解は を について解くことで得られる：

つまり

となる．DSolveで直接同じ解が得られる：

幾何学的に言えば，解 の「図」は各特性曲線で一定である：

補助条件 を満足する(49)の解を求める．(50)に を代入すると となるような が得られる．ゆえに となる．以下のようにするとDSolveで同じ解が得られる：

次のPDEを解く：

特性曲線はODE を満足する．ODEを解くと以下が得られる：

は特性曲線である．は各曲線上で定数なので （f は任意関数）となる．したがって，(51) の一般解は を について解くことで得られる：

つまり

であり，DSolveで直接同じ解を得ることができる：

定数係数初期値問題を解きたいとする[52]：

まず特性曲線を見付けるために，以下の常微分方程式の初期値問題を解く：

これに対してDSolveは次を返す：

したがって，特性曲線は以下である：

( 53 )で定義されたこの新しい座標系を使って，偏微分方程式を常微分方程式に還元する：

この初期値問題を解くと次が得られる：

それゆえ次が sτ 座標系における解である．

x と t の関数としての u を求めるために，s と τ の以下の変換を x と t について解く：

次が得られる：

したがって，答は：

となる．DSolveValueでこれと同等の形式を直接求めることができる：

3つの異なる時間における解をプロットすると次が得られる：

上のプロットは初期波 をオレンジ色で示している．時間が および に進行するに従って，波は減衰する．つまり振幅が減少するのである．また，それぞれの時間のピークがわずかに右に移動している．

非線形一階方程式—保存方程式

最初の例として，交通の流れをモデル化する問題を考える．が出口・進入ランプのないハイウェーの時間 t における地点 x での車の密度を表すとする．ハイウェーの任意の区間で u は次の方程式を満足する[54]：

ここで は流れ，つまり地点 x を通過する1分間あたりの車の台数である．上記の方程式の両辺とも，内の車の台数の変化を表す．

微分積分学の基本定理を使うと，次が得られる：

これは以下のように並べ替えることができる：

区間は任意なので，u は一次元保存方程式の解である：

引き続き保存方程式初期値問題を解く：

連鎖法則を使って，PDEを次のように書き換える：

または

ここで ．

したがって，解きたい初期値問題は以下である：

線形の場合と同様に，特性曲線法を使うと，特性曲線は次の方程式を満足する：

PDEはODEに還元される：

初期条件は以下である：

DSolveは以下で定義される特性曲線を返す：

および：

u の常微分方程式の初期値問題は以下の解を持つ：

次の式

が成り立つので，

という結果になり，もとの初期値問題(55)は暗示的に定義された次の解を持つ：

以下の初期値問題が解きたいとする：

で なので，初期値問題の陰的解は：

である．これはDSolveValueで見付かる解である：

この例では，多くの場合はできないが，x と t について明示的に について解くことができる．

次のPDEが解きたいとする：

この方程式を で以下のように書き換える：

PDEの陰的解は：

であり，これはDSolveで見付かる解である：

次はPDEの陰的解の検証である：

良設定問題

「良設定問題」とは，PDEおよびある領域における以下の基本的な特性を持つ，初期条件および／または境界条件（または他の補助条件）の集合である[56]：

1.   「存在」．すべてのPDEおよび条件を満足する少なくとも1つの解 が存在すること

2.   「一意性」．最大限1つの解であること

3.   「安定性」．一意の解 は問題のデータ上で継続的に変化する．つまりデータが少し変わると解も少し変化する．

物理的な問題がPDEでモデル化されるとき，問題が良設定となるような物理的に現実的な補助条件を持つ問題を定式化することが想定される．課される補助条件が少なすぎる場合，解は2つ以上（非一意性）になる可能性があり，問題は「劣決定問題」と呼ばれる．しかし補助条件が多すぎると解が全く存在しない（非存在）可能性があり，問題は「過剰決定問題」と呼ばれる．

良設定のPDEの概念を例示するために，次の例を見てみる．両端が指定されたように動く，外力を持つ振動する弦はこの問題を満足する[57]:

ここで である．5つの関数 ，，，，はこの問題のデータを形成する．存在と一意性は，微分可能な関数 f，φ，ψ，g，h に対して厳密に1つの解 があることを意味する．安定性はこの5つの関数のいずれかが少しでも変化すると，u もわずかに変化することを意味する．

二階線形方程式のタイプ

2つの独立変数を持つ二階線形方程式は以下の形式の方程式である[58, 59]：

ここで ，，，，，， は定数，または与えられた x と y の関数であり得る．

(60)の独立変数 および は通常空間変数を表すために使われる． の代りに時間変数 があるとしたら，(61)に項 ，， が含まれる．分類の見地からすると，これでも違いはない．物理的な意味が変わるだけである．

形式(62)の二階線形方程式には次の3つの基本的なタイプがある：

1.   「放物型」方程式（ で，標準形 に還元できるならば，熱流および拡散のプロセスを記述し特性を満足する）

2.   「双曲型」方程式（ で，標準形 または に還元できるならば，振動系および波動を記述する）

3.   「楕円型」方程式（ で標準形 に還元できるならば，定常状態現象を記述し，特性を満足する）

ここで「」は階数1か0の項を指す．これは次の例で詳しく説明する．

熱方程式

このセクションでは，熱流問題を簡単なモデルから始めてその上に構築していく形で考える．一般的な解説は熱移動モデルに関するチュートリアルでご覧いただきたい．

固定された両端温度と変数分離

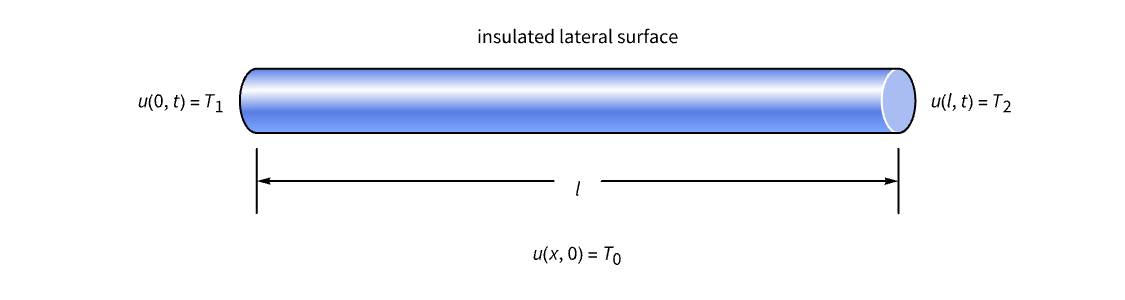
側面の境界を除く両端から熱が流入・流出できるように両側面を断熱材で包んだ長さ l の棒があるとする．この棒が温度 で固定された環境に置かれると，十分な時間経過後，棒全体の温度は安定し，その環境と同様の定常状態温度になる．それから時間 で棒をその環境から取り出し，棒の両端に温度コンポーネントを付けて両端を特定の固定温度，例えば と で維持する．棒の温度表を監視すると，一次元熱流をモデル化する基本PDEは以下になる．

PDE (63)は数量 および に関連している．前者は時間について温度変化の割合を表し，後者は温度プロファイル の凹面を表す．つまり，PDE (64)は一点における温度とその近隣の点の温度を比較するのである．比例定数 k は棒の原料となっている材質の特性である[65, 66]．

温度 は時間 の間ずっと端点 および で，に固定されていたので，境界条件について以下のことが言える：

棒が温度 に達したときからの棒の温度を監視し始めたので，初期条件は以下になる．

したがってPDE (67)，ディリクレ境界条件(68)，初期条件(69)で初期値境界値問題ができる．

まず，，つまり棒の両端が温度ゼロで保たれているとし，このときの熱流初期値境界値問題が解きたいとする：

(70)の解 は次のように書けると仮定する：

つまり解は分離可能である．

( 71 )を( 72 )に代入すると次が得られる：

(73)の両辺を で割ると以下が求められる：

は x だけの関数であり は t だけの関数なので， は定数でなければならない．

方程式(74)から2つの常微分方程式が得られる：

これについての一般解は以下になる：

ここで と は定数である．

次のステップは(75)を(76)に適用することであり，これには であることが必要である．したがって以下となる：

非自明解（ と の両方がゼロではない）に関心があるため，次のようになる：

したがって，のとき以下になる：

これらは(77)の異なる解である．

したがって，(78)には：

となるような無限に多数の解がある．ここで は定数である．線形方程式の重ね合わせの原理により，解の和も解となる．よって以下

もまた(79)および(80)の解である．

( 81 )を( 82 )に適用すると以下が得られる：

ここで は「固有値」，は固有関数と呼ばれる．

固有関数の直交性，つまり：

および：

を使うと，以下が求められる：

( 83 )を( 84 )に代入すると次のような結論になる：

これはDSolveValueが返すのと同じ解である：

ここで説明したメソッドは「変数分離法」または「固有関数展開法」という．

および の場合は非自明解にならないので，これらの場合については省略する．

ここでPDE (85), ディリクレ境界条件(86)，初期条件(87)から成る初期値境界値問題に戻ろう．この初期値境界値問題では，DSolveValueは次を返す：

，，，，のとき，解の三次元プロットは以下になる：

解のプロットをしている間に，関数TruncateSumを使うことによって総和に対する十分によい近似を得るために で無限和を打ち切った．当然 をもっと大きい値で打ち切るとよりよい近似が得られるであろう．しかしこの例では で打ち切っても目的を果たすには充分であった．

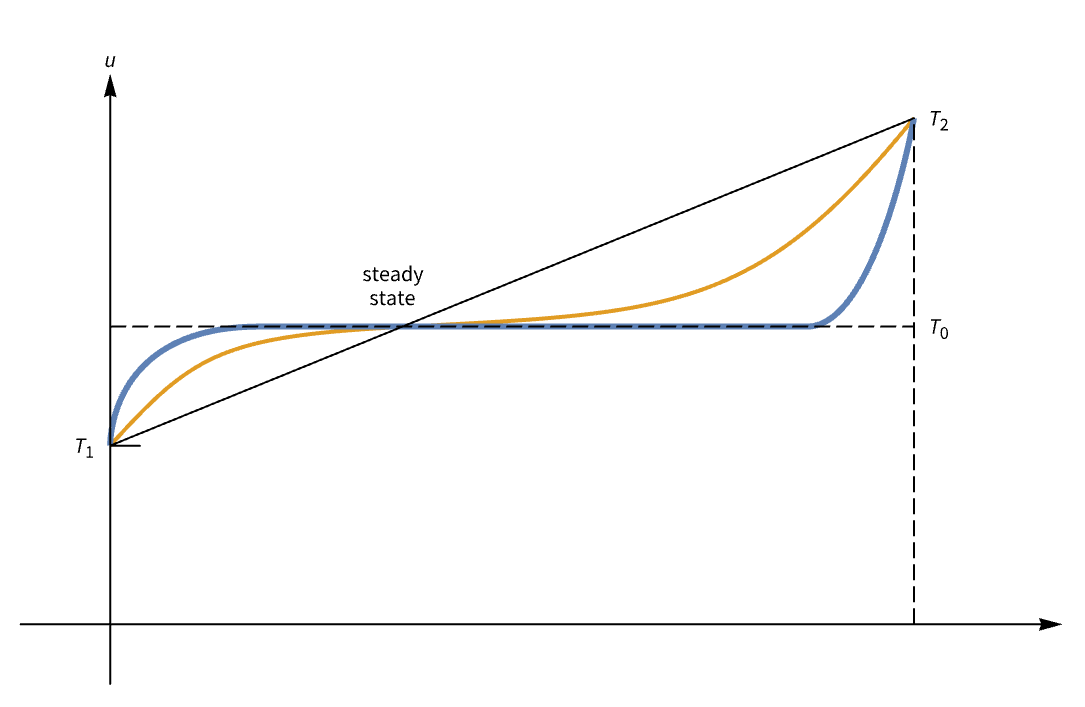
次のサブセクションでは，上の解の最初の2項が定常状態解を形成することについて見ていく．

定常状態温度

関数 が温度を表すとする．同じ環境および条件で十分な時間が経過した後，時間に伴う温度の変化がなくなっていくことが分かる．したがって，tが無限大に近づくにつれて，の極限が存在し x だけに依存すると想定できる[88]：

および以下も同様である：

定常状態温度分布関数 は，すべての について有効な境界条件(89)と熱方程式(90)を満足しなければならない．ゆえに が問題の解になる：

これは上記の初期値境界値問題の解が に近づくときの極限に等しい．

上の初期値境界値問題で ，，，，とし，具体的な値でこの問題解く：

以下のManipulate計算は，十分な時間が経過した後，解が定常状態解に収束し始めることを示している：

この計算ではQuietを使って，計算中に生成されるGeneral::munflメッセージを非表示にしている．

断熱された棒

棒の両端 ， が一定温度で保たれるのではなく，断熱される，つまりノイマン境界条件が与えられるものと仮定する．この棒の温度を記述する初期値境界値問題は以下である[91]：

この初期値境界値問題ではDSolveValueは次の解を返す：

上の初期値境界値問題で ，，とし，具体的な値でこの問題を解く：

例えば で無限和を打ち切ると，解の三次元プロットは以下になる：

熱源を持つ非斉次方程式

以下の非斉次方程式

は，すべての時間 t において棒のいたるところに内部熱源がある場合をモデル化する[92]．先の例と同じ境界条件(93)および初期条件(94)では，この場合DSolveValueは以下を返す：

上の初期値境界値問題で ，，，，，として，この問題を具体的な値で解く：

で無限和を打ち切ると，解の三次元プロットは以下になる：

電流を流すワイヤが棒を貫通していて，抵抗が一定の熱源 を生成する場合，DSolveValueは[95]を返す：

上の初期値境界値問題で ，，，，，とし，この問題を具体的な値で解く：

例えば で無限和を打ち切ると，一定の熱源 を持つこの問題の解の三次元プロットは以下になる：

拡散型の問題に対する境界条件

このサブセクションでは，ディリクレ条件，ノイマン条件，ロビン条件として与えられる境界条件を持つ初期値境界値問題の例を考える．

の一次元の棒(96)での熱流問題について，境界の温度が指定される，つまり両端の条件がディリクレ条件で与えられ，初期条件が で与えられるとする[97]：

例えば で無限和を打ち切ると，解の三次元プロットは以下になる：

初期条件 ：

境界条件 および ：

これらは解で満足される．

で である一次元の棒(98)上で熱源を持つ熱流問題について，境界における温度の流れが指定される，つまり両端の条件がノイマン条件で与えられ，初期条件が で与えられるとする[99]：

例えば で無限和を打ち切ると，解の三次元プロットは以下になる：

で である一次元の棒(100)上で熱源を持つ熱流問題について，一端の境界の温度と他方の端の温度の流れが指定される，つまり一端 の条件がディリクレ条件で与えられ，他方の端 の条件がノイマン条件で与えられるとする．また，初期条件が で与えられるとすると，以下が得られる[101]：

例えば で無限和を打ち切ると，解の三次元プロットは以下になる：

で である一次元の棒(102)上で熱源を持つ熱流問題について，境界の一端の温度と他方の端の周囲媒体の温度が指定される，つまり一端 の条件がディリクレ条件で与えられ，他方の端 がロビン条件で与えられるとする．この問題では，棒の終点 は決められた温度の周囲媒体に接している[103]．つまり，右端は対流熱伝達にさらされているのである[104]．また，初期条件が であるとすると，以下が得られる：

上の解は変数分離法の結果であるため，無限和には固有値 に対応する固有関数上の和が関わっている．固有値はこの条件によって定義される[105]：

解をプロットするために，解の無限和について十分によい近似がえられるようとなるような固有値を計算する：

となるような固有値は503個ある．

次に，最初の503個の固有値に対応する上の解の和を計算する：

打ち切られた解の三次元プロットは次になる：

で である一次元の棒(106)上で熱源を持つ熱流問題について，一端の温度の流れが指定され，他方の端が他の媒体と接触する，つまり一端 の条件がノイマン条件で与えられ，他方の端 がロビン条件で与えられるとする．また，初期条件が で与えられるとすると，以下が得られる[107]：

となるような固有値を計算する：

となる固有値は504個ある．

次に最初の504個の固有値に対応する上記の解の和を計算する：

打ち切られた解の三次元プロットは以下になる：

で である一次元の棒(108)上で熱源を持つ熱流問題について，両端が別の媒体に接している[109]，つまり両端の境界条件がロビン条件で与えられるとする．また，初期条件が で与えられるとすると，以下が得られる：

となるような固有値を計算する：

となるような固有値は504個ある．

次に，最初の504個の固有値に対応する上記の解の和を計算する：

打ち切られた解の三次元プロットは以下になる：

周囲媒体への熱損失

棒の両端の温度が固定されている均一の棒が媒体で囲まれていて，棒の外側面から周囲媒体への熱損失が起こるとする．この状態を記述する熱流偏微分方程式は以下である：

ここで項 は側面境界からの熱損失である[110]．

，，のとき，棒の両端の温度がゼロに固定されていて，初期温度分布が で与えられるとすると，次の熱流問題になる：

この初期値境界値問題ではDSolveValueは以下を返す：

例えば で無限和を打ち切ると，解の三次元プロットは以下となる：

同じ初期条件と境界条件で熱損失項がない場合，DSolveValueは次を返す：

熱損失項の影響を見るために，解を隣り合せにプロットする：

半無限棒における拡散問題

上の問題はすべて，有限区間を対象とした．考慮する棒が非常に長い場合は，それを半無限，つまりとして扱うことができる．棒が均一で外部の熱源がない場合は，を記述する偏微分方程式は以下のままである[111, 112]：

温度は において一定，，に保たれる．もう一方の境界がないため，他の境界条件はない．しかし のとき は有限，つまり有界のままであると想定する．したがってこのモデルは以下のようになる：

，，のとき，DSolveValueは次を返す：

AssumptionsはDSolveValueのオプションであり，上の計算では独立変数 x の領域を指定するために使われている．

解の三次元プロットは以下である：

における境界条件はノイマン条件で与えられる：

解の三次元プロットは以下である：

無限棒における拡散問題

非常に長い棒の中心で熱伝導を調べたいとする．この場合，棒はからに及ぶものと想定する．したがって境界条件はなく，解く問題は以下になる[113]：

，のとき，DSolveValueは次を返す：

解の三次元プロットは以下である：

システムの中に熱を生成する熱源があるとする：

解の三次元プロットは以下である：

難しい方程式を簡単なものに変換する

拡散対流方程式[114]：

は十分に研究された熱方程式

に変換することができる．次の変換法を使う：

もちろんこの問題の初期条件と境界条件も同じ変換法を使って変換しなければならない．の初期値境界値問題があるとする．ここで初期条件は となるように与えられ，両端のディリクレ境界条件は となるように与えられる．この初期値境界値問題では，DSolveValueは次を返す：

例えば で無限和を打ち切ると，解の三次元プロットは以下である：

フーリエ変換と熱方程式

初期温度 が既知である無限棒における熱流を考える．初期値問題が解きたいとする：

これはコーシー(Cauchy)問題とも呼ばれる[115]．

まず として，方程式を変換する：

次に初期条件 を変換する：

これで初期条件を持つ の常微分方程式になる．この常微分方程式の初期値問題を解くと，次が得られる：

上の解をもとに変換すると，もとの偏微分方程式の初期値問題の解が得られる：

解にExpToTrigを適用して簡約すると，次が得られる：

DSolveValueで直接同じ解が得られる：

解の三次元プロットは以下である：

ラプラス(Laplace)変換と熱方程式

熱が出たり入ったりしないように曲面が完全に断熱された長さ の丸棒があるとする．時間 における棒の温度は , で与えられる．のとき，棒の両端の温度は と で与えられる．棒の温度 の初期値境界値問題は以下になる[116]：

まず として，LaplaceTransformを使って偏微分方程式を常微分方程式に変換する：

初期条件 が上のReplaceAllで使われている．

境界条件を変換すると以下が求められる：

常微分方程式の初期値問題を解く：

ここで上の解をもとに変換すると，もとの初期値境界値問題の解が得られる：

DSolveValueで同じ解が直接得られる：

解の三次元プロットは以下である：

二次元熱方程式

でである有限の二次元領域上の薄い長方形板における温度分布 を調べるとする．ここで板の外側面は断熱されているため外側面からの熱損失はない．境界 および は固定温度ゼロに保たれる（ディリクレ条件）．境界 は断熱されており（ノイマン条件），境界 は温度ゼロの周囲媒体に接している（ロビン条件）．このシステムには熱を生成する熱源はない．初期温度分布は で与えられ，板の素材の一定の熱特性は である．したがって，解く初期値境界値問題は以下になる[117]：

この初期値境界値問題では，DSolveValueで解が求められる：

となるような固有値を計算する：

となる固有値は100個ある．

次に，最初の100個の固有値に対応する上の解の和を計算する：

解の三次元プロットを可視化する：

三次元熱方程式

，，の直方体の形の立体における温度分布 を調べるとする．境界 ，，，は固定温度0度に保たれる．境界 は断熱されていて，境界 は温度ゼロの周囲媒体に接している．このシステムには熱を生成する熱源はない．初期温度分布は で与えられ，立体の素材の一定の熱特性は である．したがって，解きたい初期値境界値問題は以下になる[118]：

この初期値境界値問題では，DSolveValueで解が求められる：

となるような固有値を計算する：

となるような固有値は202個ある．

最初の202個の固有値に対応する上の解の和を計算し，例えば で無限和を打ち切る：

のときの解の三次元等高線プロット：

極座標と円筒座標における熱流初期値境界値問題

このサブセクションでは，円形および円筒領域における熱流初期値境界値問題を調べる．円形領域では，まず円対称，つまり角度依存性のない場合を考えてから2つ目の例で角度依存性のある場合を考える．3つ目の例では円筒領域における熱流方程式を扱う．

半径 r の薄い円板における熱伝導を調べるとする．また，このシステムは円対称であり，熱係数は空間的に不変で，熱源はないものとする．よって，扱う偏微分方程式は以下になる[119]：

有限区間でこの偏微分方程式の解が欲しいとすると，の有界性，つまり≤M, ∀_tt>0となるような∃_Mが必要になる．のとき，以下の境界条件：

および以下の初期条件があるとする：

DSolveValueはこの初期値境界値問題に以下の解を返す：

解の三次元プロットは以下である：

円形領域 における解の三次元プロットは以下である：

二次元領域， 上で，熱源のない半径 r の薄い円板における温度分布 を調べるとする．また，円板は非常に薄いとする．よって， z 依存性は無視でき，扱う偏微分方程式は以下になる[120]：

境界条件の一つは の有界性が必要というものである．のとき，以下の境界条件：

があり，以下の初期条件があるとする：

DSolveValueはこの初期値境界値問題に以下の解を返す：

実用的な目的のために，上の解でに設定しなければならない．および について最初の50個の固有値 を計算する必要がある：

これら50個の固有値を使って，和を計算する：

解の三次元プロットを可視化する：

解の三次元プロットを円筒領域で可視化する：

，，の三次元領域における半径 r の円筒の温度分布 を調べるとする．ここで扱う偏微分方程式のは以下である[121]：

境界条件の一つは の有界性が必要であるというものである．のとき，以下の境界条件：

があり，以下の初期条件があるとする：

DSolveValueはこの初期値境界値問題に以下の解を返す：

実用的な目的のために，例えば で無限和を打ち切る：

のときの解の三次元等高線プロットを可視化する：

波動方程式

このセクションでは，波動現象問題を簡単な問題から始めてその上に構築していく形で考える．一般的な解説は波動方程式に関するチュートリアルでご覧いただきたい．

一次元波動方程式

長さ l の弦の小さい振動を考えるとする．弦は両端が固定されていて，弦の振動は平面で起こる，つまり変位は減と並行であると仮定する．平衡からの弦の縦方向変位 を監視すると，弦の縦振動およびねじり振動をモデル化する基本の偏微分方程式は波動方程式である[122]：

ここで c は材質の線形密度に関連する一定の物理的パラメータであり[123]，波の速さとも呼ばれる[124]．項 は弦の張力による合力を表す．波動方程式には二階時間微分 が含まれているので，について一意に解を定義するためには，方程式に2つの初期条件が必要になる：

これは1つの初期条件しか必要ではなかった熱方程式問題とは異なる[125]．

例として，長さ1，の弦があり，以下の微分方程式，境界条件，初期条件で初期値境界値問題が構成されるとする：

これについてDSolveValueは以下を返す：

例えば で無限和を打ち切ると，x のさまざまな値に対する解の二次元プロットは以下になる：

ダランベール(D'Alembert)の解

初期データで波動方程式(126)の解を直接求めることが可能な場合がある．，，とすると，波動方程式(127)は以下になる[128]：

DSolveはこの新しい偏微分方程式に以下の解を返す：

ゆえに，もとの変数に変換し直すと，波動方程式(129)の解は以下になる：

同等の解の形式はDSolveValueで直接求めることができる：

次に，無限に長い弦の波動方程式に初期条件を課して解を求めると，初期データについての解が得られる：

この解はダランベールの解または進行波解と言われ，一方は左に他方は右に伝搬速度 c で動く2つの波の重ね合わせとして解を表す．この形式の解は，初期データが後に解にどのような影響を与えるかを示す[130]．

一次元波動方程式の一般化：電信方程式

今回は，モデルに減衰効果があり，システムに作用する外力もあるものとする．また，弦の変位とは逆向きの復元力もあるとする．このとき波動現象をモデル化する偏微分方程式は以下になる：

ここで は空間-時間依存の波の振幅，c は波の速さ，β は復元力係数，γ は媒体の減衰係数，は外力を表す．偏微分方程式(131)は「電信方程式」としても知られている．媒体が均一であると仮定すると，既出の係数はすべて空間的に不変であり定数として書くことができる[132, 133]．

以下のように

とすると，DSolveValueは次を返す：

例えば で無限和を打ち切ると，解の三次元プロットは以下になる：

非斉次境界条件

境界で与えられるソース，つまり非斉次境界条件が与えられる問題を考えてみる．次のような初期値境界値問題があるとする[134]：

この初期値境界値問題について，DSolveValueは以下を返す：

例えば で無限和を打ち切ると，以下が得られる：

打ち切られた解の三次元プロットは，以下である：

無限領域内の波動方程式

このサブセクションでは，半線および全線上の波動現象問題を考える．

以下の問題：

を半線上で考えると，DSolveValueは以下を返す[135]：

解の三次元プロットは以下のようになる：

以下の問題：

を全線上で考えると，DSolveValueは以下を返す[136]：

解の三次元プロットは以下のようになる：

以下の非斉次初期値問題：

を全線上で考えると，DSolveValueは以下を返す[137]：

ListPlotで使うために，解からデータ点のリストを作成する：

ListPlotを使うと，以下の三次元プロットが求められる：

波動方程式に関連する境界条件

このサブセクションでは，ディリクレ境界条件，ノイマン境界条件，ロビン境界条件を持つ，波動現象初期値境界値問題を考える．

有限の弦の振動問題について，制御された端点を持つ，つまり両端の条件がディリクレ条件で与えられるとする[138]：

例えば で無限和を打ち切ると，解の三次元プロットは以下のようになる：

弦の両端が摩擦のないスリーブ上で垂直にスライドすることができる，つまり両端の条件がノイマン条件で与えられる境界上で力が指定される有限の弦上の振動問題があるとする[139]：

例えば で無限和を打ち切ると，解の三次元プロットは以下のようになる：

有限の弦の振動問題について，一端は制御され，もう一方の端には力が指定されている，つまり一端の条件はディリクレ条件で与えられ，他方の端はノイマン条件で与えられるとする[140]：

例えば で無限和を打ち切ると，解の三次元プロットは以下のようになる：

有限の弦の振動問題について，一端は制御され，他方の端には伸縮素材が付いている，つまり一端の条件はディリクレ条件で与えられ，他方はロビン条件で与えられるとする[141]：

となるような固有値を計算する：

となるような固有値は202個ある．

次に，最初の202個の固有値に対応する上の解の和を計算する：

打ち切られた解の三次元プロットは以下のようになる：

有限の弦の振動問題について，両端に伸縮素材が付いている，つまり両端の条件はロビン条件で与えられるとする[142]：

となるような固有値を計算する：

となるような固有値は403個ある．

次に，最初の403個の固有値に対応する上の解の和を計算する：

打ち切られた解の三次元プロットは以下のようになる：

フーリエ変換と波動方程式

無限に長い弦の振動を記述する，以下の初期値問題が解きたいとする[143]：

まず として方程式を変換する：

次に初期条件を変換する：

これで初期条件を持つ の常微分方程式になった．この常微分方程式初期値問題を解くと，以下が得られる：

ここで上記の解を変換し直すと，もとの偏微分方程式初期値問題の解が得られる：

この解にExpToTrigを適用して簡約すると次になる：

これと同じ解をDSolveValueで直接求めることができる：

解の三次元プロットは以下のようになる：

ラプラス変換と波動方程式

振動を記述する以下の初期値境界値問題が解きたいとする[144]：

まずLaplaceTransformを使って として，偏微分方程式を常微分方程式に変換する：

上のReplaceAllでは，初期条件 および が使われている．

この境界条件を変換すると次になる：

常微分方程式の初期値問題を解く：

ここで上の解をもとに変換し直すと，もとの初期値境界値問題の解が得られる：

同じ解がDSolveValueで直接求められる：

解の三次元プロットは以下のようになる：

二次元波動方程式

および である有限の二次元矩形領域における薄い長方形膜の横振動を調べるとする．膜は減衰のない媒体の中にあると仮定する．また，境界は固定されていて，膜の初期変位は ，初期速度は とする．このシステムに作用する外力はなく，波の速さは である．したがって，横波の振幅 を表す，解くべき初期値境界値問題は以下になる[145, 146]：

この初期値境界値問題について，DSolveValueは次の解を見付ける：

例えば で無限和を打ち切る：

ここで解の三次元プロットを可視化する：

三次元波動方程式

，，である直方体における振動を調べるとする．媒体には減衰はないと仮定する．また，境界は固定されていて，オブジェクトの初期変位は ，初期速度は とする．このシステムに作用する外力はなく，波の速さは である．ここで波の振幅 を求める．ゆえに解くべき初期値境界値問題Weは以下になる[147, 148]：

この初期値境界値問題について，DSolveValueは以下の解を見付ける：

例えば で無限和を打ち切る．

のとき：

解の三次元等高線プロットは以下のようになる：

円形膜の対称振動

半径が a で，端が固定されている円形膜の変位を記述する問題を考える．まず，初期条件が θ と無関係の簡単な場合を扱う．変位を定義する次の波動方程式[149]：

は，極座標において：

となる．

が有界であると仮定して，半径1の円形膜における以下の初期値境界値問題を解く：

例えば で無限和を打ち切ると，解の三次元プロットは以下のようになる：

振動するドラムの皮

半径 a の円形ドラム の振動を調べるとする．二次元波動方程式[150]：

は極座標において で：

となる．

が有界であると仮定して，半径2の円形ドラムにおける以下の初期値境界値問題を解く：

例えば で無限和を打ち切ると，次が得られる：

ここで解の三次元プロットを可視化する：

解の三次元プロットを で可視化する：

角度周期を持つ円形膜の振動

が有界であると仮定して，以下の初期値問題および境界値問題について角度周期を持つ円形膜の振動を考えると，DSolveValueは次を返す[151]：

実用的な目的のために，上の解の例えば で無限和を打ち切る．ここで for および の最初の50個の固有値を求める必要がある：

これら50個の固有値を使って和を計算する：

解の三次元プロットを可視化する：

の解の三次元プロットを以下で可視化する：

ポテンシャル方程式またはラプラス(Laplace)方程式

二次元の定常状態温度分布のラプラス方程式は以下である：

方程式(152)二次元膜の時間依存平衡状態も表すため，二次元では熱方程式と波動方程式両方についてのかなりの共通部分である．関数のラプラシアンは，隣接する点における関数の値の平均から，ある点における関数の値の偏差を示す．例えば，定常状態で伸びて動かないゴム膜はラプラス方程式を満足するため，任意の点における膜の高さは付近の点における膜の高さの平均に等しい[153, 154]．

「ポアソン方程式」は=f である．ここで，f 空間変数のみの関数であり，次のようないくつかの物理現象の特性を示す[155]：

三次元における等価のラプラス方程式方程式は以下である：

長方形内のポテンシャル

長方形内のディリクレ問題は，数学物理学における初歩的で有名な問題の一つである．電荷のない矩形領域における静電ポテンシャルが調べたいとする[156]：

この境界値問題について，DSolveValueは以下を返す：

例えば で無限和を打ち切ると，解の三次元プロットは以下になる：

長方形内のその他のポテンシャル境界値問題の例

このサブセクションでは，境界の条件がディリクレ条件，ノイマン条件，ロビン条件で与えられた境界値問題の例を考える．

境界条件にディリクレ条件とノイマン条件の両方が関わっているとする[157]：

例えば で無限和を打ち切ると，解の三次元プロットは以下になる：

境界条件にディリクレ条件，ノイマン条件，ロビン条件が関わっているとする[158]：

実用的な目的のために，上の解で例えば で無限和を打ち切る．したがって，に対する最初の200個の固有値 を計算する必要がある：

これら200個の固有値を使って和を計算する：

打ち切られた解の三次元プロットは以下のようになる：

無界領域上のポテンシャル

このサブセクションでは，上半平面，右半平面，無限板，半無限垂直板，半無限水平板上のポテンシャル問題を考える．

が無限の半平面上で絶対可積分であると仮定して，上半平面上の定常状態温度分布を考える．したがって，境界値問題は次になる[159]：

これについて，DSolveValueは次を返す：

解の三次元プロットは以下のようになる：

が無限の半平面上で絶対可積分であると仮定して，右平面上の定常状態温度分布を考える．したがって，境界値問題は次になる[160]：

これについて，DSolveValueは次を返す：

解の三次元プロットは以下のようになる：

が無限の薄い板上で絶対可積分であると仮定して，外側面が断熱された薄い板における定常状態温度分布を考える．したがって，境界値問題は次になる[161]：

これについて，DSolveValueは次を返す：

NIntegrateを使って，解のデータ点のリストを計算する：

ListPlot3Dを使った解の三次元プロットは以下のようになる：

が半無限の板上で絶対可積分であると仮定して，この半無限垂直板における定常状態温度分布を考える．したがって，境界値問題は次になる[162]：

これについて，DSolveValueは次を返す：

のときの解の三次元プロットは以下のようになる：

のときの解の三次元プロットは以下のようになる：

が半無限の板上で絶対可積分であると仮定して，この半無限水平板における定常状態温度分布を考える．したがって，境界値問題は次になる[163]：

これについて，DSolveValueは次を返す：

のときの解の三次元プロットは以下のようになる：

のときの解の三次元プロットは以下のようになる：

非斉次境界条件

ソースが境界で動作する問題を考える[164]：

非斉次境界条件を持つこの境界値問題について，DSolveValueは次を返す：

例えば で無限和を打ち切ると，解の三次元プロットは以下のようになる：

極座標のラプラス方程式

このサブセクションでは，極座標におけるポテンシャル境界値問題を考える．

ポテンシャルが境界上で与えられるとき，円内部の静電ポテンシャルを記述する内部ディリクレ問題が解きたいとする[165]:

この境界値問題について，DSolveValueは次を返す：

解の三次元プロットは以下のようになる：

円領域 における解の三次元プロットは以下のようになる：

ポテンシャルが境界上で与えられるとき，2つの円の間，つまり円環内の内部ディリクレ問題が解きたいとする[166]：

この境界値問題について，DSolveValueは次を返す：

解の三次元プロットは以下のようになる：

円領域 における解の三次元プロットは以下のようになる：

原点の温度が有限であると仮定して，外側面が断熱されて周期的境界条件を持つ，円筒領域上の薄い板の定常状態温度分布を調べるとする[167]：

解の三次元プロットは以下のようになる：

円形領域 における解の三次元プロットは以下のようになる：

原点の温度が有限であると仮定して，外側面が断熱された，円筒領域上の薄い板の定常状態温度分布を調べるとする[168]：

解の三次元プロットは以下のようになる：

円形領域 における解の三次元プロットは以下のようになる：

円板内で作用する強制項に反応する円板のポテンシャルが求めたいとする．したがって半径 a の円板上で非斉次境界条件を持つ非斉次ラプラス偏微分方程式の境界値問題となる．これについて，DSolveValueは次を返す[169]：

，，ならば，次が得られる：

解の三次元プロットは以下のようになる：

円形領域 における解の三次元プロットは以下のようになる：

球座標のラプラス方程式

このサブセクションでは，球座標におけるポテンシャル境界値問題を考える．

異なる温度に保たれている2つの球の間の定常状態温度が求めたいとする[170]：

この境界値問題について，DSolveValueは次を返す：

，，，のとき，以下のようになる：

温度（θ だけに依存する）が境界上で指定されているとき，球内の定常状態温度が求めたいとする[171]：

この境界値問題について，DSolveValueは次を返す：

および のとき，以下のようになる：

3Dにおけるラプラス問題

直方体におけるラプラス問題を考えるとする[172]：

例えば で無限和を打ち切ると，解の三次元等高線プロットは以下のようになる：

非線形偏微分方程式

重ね合わせの法則は非線形方程式には当てはまらないので，固有関数法および変換法が適用できない．しかし，非線形問題を扱う方法はたくさんある．

衝撃波と膨張波の解

初期データが2つの定常状態 および で形成され，で跳躍不連続点を持つ初期値問題を「リーマン(Riemann)問題」という．ここでリーマン問題を持つバーガース(Burgers)方程式を考える[173, 174]：

ここで初期条件は以下で与えられる：

のとき，特徴方程式は交わるので，滑らかな解は構築できない．その代りに，ランキン・ユゴニオ(Rankine–Huguenot)条件によって決定される速度で移動する衝撃波の形式の弱解を構築することができる． のとき，単純波理論から膨張波の形式の弱解が構築できる：

u(x,0)=のとき，以下の衝撃波解が得られる：

これについての解の三次元プロットは以下のようになる：

一方，u(x,0)=のとき膨張波解が得られる：

これについての解の三次元プロットは以下のようになる：

乱流理論の一般化された粘性バーガース方程式 [175]を考える：

ここで初期条件は以下で与えられる：

この初期値境界値問題について，DSolveValueは次を返す：

ϵ が正の値のときは解は滑らかである：

ϵ が0に近付くとき，解はショック不連続性を示す：

シャルピー(Charpit)の解法

以下の形式の についての一階偏微分方程式があるとする[176]：

ここで ， である．ここで目標とするのは，方程式(177)と同じ解を持つ，形式 （は定数）の別の方程式を見付けることである．そのためにこれら2つの方程式を組み合せ，p と q について解き，その後以下の「パッフ(Pfaffian)微分方程式」を u について解く：

と の解が同じであり(178)が積分可能でなければならないという必要条件は以下の適合条件を導く：

条件(179)は特性方程式（シャルピー方程式）を導く：

p か q，またはその両方を含む(180)の積分のいずれかが求められるならば，この積分を追加の微分方程式， として取り，p と q について解いて(181)を積分可能にすることができる：

(182)を積分することで(183)の解が与えられる．

パッフ微分方程式(184)を解くと，(185)の完全積分になる．関数CompleteIntegralは一階偏微分方程式の完全積分を直接返す．

以下の非線形微分方程式があるとする：

(186)から以下のようになる：

(187)の等式を使うと，以下が得られる：

(188)を使って u について(189)を解くと，求めたい解が得られる：

DSolveもこの偏微分方程式について同じ解を与える．(190)と一致する：

CompleteIntegralでも同じ完全積分が与えられる：

ヤコビ(Jacobi)の方法

以下の形式の についての一階偏微分方程式があるとする[191]：

ここで ，，である．ここで目標とするのは，方程式(192)と同じ解を持つ，形式 および の2つの別の方程式を求めることである．このためにこれら3つの方程式を組み合せ，，，について解き，その後以下の「パッフ(Pfaffian)微分方程式」を u について解く：

と の解が(193)の解と同じでなければならないという必要条件は以下の適合条件を導く：

ここではポアソン(Poisson)カッコである．

条件(194)は特性方程式を導く：

(195)の積分，つまり と を求め，が検証できるならば，，，について以下を解き，(196)を積分可能にすることができる：

(197)を積分すると(198)の解が与えられる．

この方法は3個以上の独立変数を持つ一階偏微分方程式に適用できる．

シャルピーの解法と同様に，パッフ微分方程式(199)を解くと(200)の完全積分になる．これはCompleteIntegralで直接計算することができる．

以下の非線形微分方程式があるとする：

したがって，(201)から以下のようになる：

である．(202)と(203)を ，，について解くと，以下が得られる：

(204)で求められたものを使うと，パッフ微分方程式(205)は次のようになる：

(206)を積分すると以下が得られる：

DSolveもこの偏微分方程式ついて同じ解を与える．(207)と一致する：

CompleteIntegralでも同じ完全積分が与えられる：

進行波解

進行中の基準系 では，新しい独立変数，例えば を導入することで， の多項式偏微分方程式を新しい独立変数 の常微分方程式に変換することができる．の導関数はの多項式，つまり なので， の導関数はすべて の多項式である．したがって，連鎖法則を使って，多項式偏微分方程式は の多項式係数を持つ の常微分方程式変換されるのである．それから常微分方程式の多項式解を求め，すべての解の集合の部分集合が生成できる．ここでの引数は他の双曲三角関数の解をカバーするように一般化することができる[208]．

お馴染みの以下のKdV方程式は：

運河の浅水波やプラズマ中のイオン音波をモデル化する[209]：

初期条件および境界条件が存在するとする：

以下は解のプロットの可視化である：

実数パラメータ を持つ従来のブシネスク方程式：

は，波長が水深に比べてかなり大きい水面波を記述するためにブシネスクによって提唱された[210]：

とすると，初期条件および境界条件が存在する：

以下は解のプロットの可視化である：

カドムツェフ・ペトビアシュビリ(KP)方程式は2つの空間座標と1つの時間座標の非線形偏微分方程式であり，横軸座標に遅い依存性を持つ小さい振幅の非線形の長い波の進化をモデル化する[211]：

の場合はKPII方程式として知られており，例えば表面張力の小さい水の波をモデル化する． の場合はKPI方程式として知られており，表面張力の大きい薄膜の波をモデル化するのに使われる．

KP方程式は，KdV方程式が空間一次元の可積分方程式とみなされるのと同じように，空間二次元の可積分方程式とみなされる．KP方程式は，ラックスペアの適合形式の系として書かれることがよくある：

これについてDSolveは次を返す：

KPII（つまり ）を考えると，初期条件および境界条件がある：

以下は解の三次元プロットの可視化である：

以下のKdV–ZK方程式[212]，

は，陰イオンを含む多成分磁化プラズマ中のイオン音波をモデル化する：

とすると，初期条件と境界条件が存在する：

応用

このセクションでは，物理，工学，金融等の問題への偏微分方程式初期値境界値問題の応用を考える．

振動梁（四階偏微分方程式）

バイオリンの弦の横振動とは反対に，薄い梁の横振動は曲げ抵抗性を示す．この抵抗性が波動方程式を四階梁方程式に変化させる：

ここで は梁の線形密度に対する剛性定数の比である[213]．

両端が固定されているが端点における勾配は動く薄膜の小さい振動を考えるならば，で表される梁の曲げモーメントは端点ではゼロでなければならない．したがって，次の初期条件と境界条件があることになる[214]：

例として，長さが1，の梁があるとすると，次の偏微分方程式，境界条件，初期条件で初期値境界値問題ができる：

これについて，DSolveValueは次を返す：

解の三次元プロットは以下のようになる：

ブラック・ショールズ(Black–Scholes)方程式

原資産価格がリスク中立型と想定されるとき，すべてのヨーロピアンオプションはブラック・ショールズ偏微分方程式を満足する．が原資産 ，経過時間 ，無リスク金利 ，配当率 ，資産価格の予想変動率，つまり年率標準偏差が であるオプションの価格だとすると，すべてのヨーロピアンオプションをモデル化する方程式は以下になる[215]：

がストライクプライス， が満期日とすると，プットオプションの初期条件は以下で与えられる[216]：

このプットオプションの問題について，DSolveValueは次を返す：

このプットオプションの場合，境界条件は陰的に以下として取られる：

パラメータの典型的な値に対するオプション値を計算する：

FinancialDerivativeで与えられる値と比較する：

コールオプションに対する初期条件は[217]として与えられる：

コールオプション問題では，DSolveValueは次を返す：

コールオプションでは，境界条件は陰的に以下のように取られる：

パラメータの典型的な値に対するオプション値を計算する：

FinancialDerivativeで与えられる値と比較する：

シュレーディンガー(Schrödinger)方程式

量子力学において，質量 m の自由粒子の運動は時間依存シュレーディンガー方程式で記述される：

ここで はプランク(Planck)定数を で割ったもの，u は粒子の運動を記述する波動関数である[218]．

以下の初期値境界値問題について，DSolveValueは以下を返す：

と仮定すると，解の三次元プロットは以下のようになる：

球面調和関数

ポテンシャル が境界上に与えられているときに，半径3の球内部のポテンシャルを求めたいとする．これについては，方位対称ではない球におけるラプラス偏微分方程式境界値問題を解かなければならない[219]：

打ち切られた解を定義する：

より大きい の値において和を打ち切っても同じ解が得られる：

以下は解の球面三次元プロットの可視化である：

偏微分方程式系

多くの物理系は単独の偏微分方程式では記述できないが，偏微分方程式系でモデル化される．これらの方程式では，圧力，密度，温度，それらの偏導関数等の未知の関数が物理法則によって記述され，その関数すべてが同時に見付けようとされる[220]．

偏微分方程式系を調べる別の理由として，単独の高階偏微分方程式を一階偏微分方程式系として書くことができることがよくあるというものがある[221]．

定数係数偏微分方程式系の以下の初期値境界値問題について，DSolveは次を返す：

，のとき，以下となる：

の三次元プロットは以下のようになる：

の三次元プロットは以下のようになる：

変数係数非斉次偏微分方程式系の以下の初期値境界値問題について，DSolveValueは次を返す：

の三次元プロットは以下のようになる：

の三次元プロットは以下のようになる：

モデル化

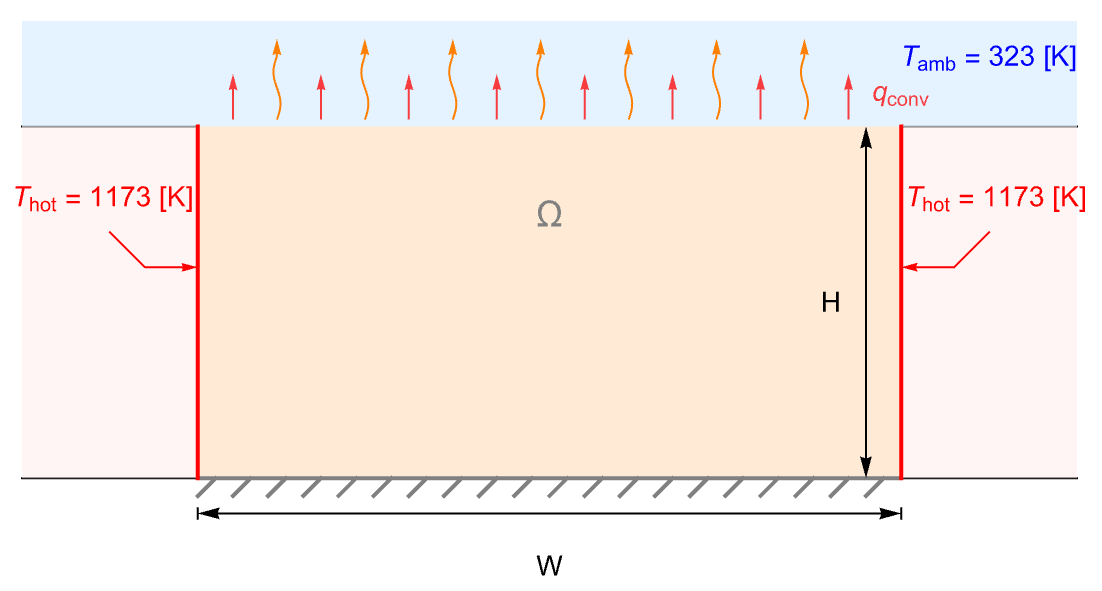
熱工学における熱移動はエネルギーの伝達のモデル化に関心がある．基本的な熱伝達の例題をわずかに修正したものを解いてみよう：

幅 ，高さ のモデル領域Ωは高熱伝導性素材に埋め込まれたセラミック板である．板の側面の境界は一定温度 で維持される．板の上面は熱対流と熱放射によって の周囲環境に熱を失っている．しかし底面境界は断熱されていると想定する．

ここでの目標は，セラミック板の定常状態温度分布を求めることである．

幅 ，高さ の矩形領域を設定する．

セラミック板の熱伝導率 k，熱移動係数 h，密度 ρ，熱容量 および放射率 ε は以下で与えられる：

モデルパラメータを定義する：

左右の境界に温度面境界条件を設定する：

上面に対流境界条件を設定する：

残りの底面境界には，デフォルトの断熱境界条件が適用される：

NDSolveValueとDSolveValueを使って熱移動PDEモデルを解く：

定常状態温度分布を可視化する：

まとめ

このモノグラフでは，偏微分方程式，初期値境界値問題，およびこれらの問題を解くためにDSolveとDSolveValueで利用できるメソッドについての概要を説明した．

参考文献

1.  Strauss, W. Partial Differential Equations: An Introduction. (2nd ed.) John Wiley & Sons, Inc., 2008.

2.  Farlow, S. J. Partial Differential Equations for Scientists and Engineers. Dover Publications, Inc., 1993.

3.  Powers, D. L. Boundary Value Problems and Partial Differential Equations. (6th ed.), 2010.

4.  Trim, D. W. Introduction to Complex Analysis and Its Application. (1st ed.) PWS Pub. Co., 1996.

5.  Evans, L. C. Partial Differential Equations. (2nd ed.) American Mathematical Society, 2010.

6.  Zwillinger, D. Handbook of Differential Equations. (3rd ed.) Academic Press, 1997.

7.  Baldwin, D., Göktaş Ü., Hereman W., Hong L., Martino R. S. and Miller J. C. "Symbolic Computation of Exact Solutions Expressible in Hyperbolic and Elliptic Functions for Nonlinear PDEs." Journal of Symbolic Computation 37, no. 6 (2004): 669–705.

8.  Kelly, M. "Evaluation of Financial Options Using Radial Basis Functions in Mathematica." The Mathematica Journal 11, no. 3 (2010): 333–257.

9.  Deconinck, B., Drogdon T. and Vasan V. "The Method of Fokas for Solving Linear Partial Differential Equations." SIAM Review 56 (2014): 159–186.

10.  Stavroulakis I. P. and Tersian S. A. Partial Differential Equations—An Introduction with Mathematica and Maple. (2nd ed.) World Scientific Pub. Co. Re. Ltd., 1999.