CompleteIntegral

CompleteIntegral[pde,u,{x1,…,xn}]

gives a complete integral u for the first-order partial differential equation pde, with independent variables {x1,…,xn}.

Details and Options

  • A complete integral of a first-order partial differential equation (PDE) in n variables is a solution that depends on n independent arbitrary constants c1,c2,…,cn.
  • A complete integral is typically used to generate a complete set of solutions to the PDE.
  • A solution to the PDE that satisfies a specific initial condition can be obtained by constructing the envelope of a smoothly varying subfamily of simple solutions that depend on 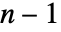parameters, as illustrated. »
  • The output from CompleteIntegral is controlled by the form of the dependent function u or u[x1,…,xn], as in DSolve.
  • CompleteIntegral can give implicit solutions in terms of Solve.
  • CompleteIntegral can give solutions that include Inactive sums and integrals that cannot be carried out explicitly. Variables K[1], K[2], … are used in such cases.
  • Boundary conditions for the PDE can be specified to obtain specific solutions of the PDE that are free from the arbitrary constants in the complete integral. »
  • The following options can be given:
  • Assumptions$Assumptionsassumptions on parameters
    GeneratedParametersChow to name generated parameters
    MethodAutomaticwhat method to use
  • GeneratedParameters controls the form of generated parameters; these are by default constants C[n].

Examples

open allclose all

Basic Examples  (3)

Find a complete integral of a partial differential equation:

Plot the solution for particular values of the arbitrary constants:

Get a "pure function" complete integral for w:

Substitute the solution into an expression:

Complete integral of a partial differential equation in 3 dimensions:

Now add conditions:

Scope  (5)

Find the complete integral of a partial differential equation in 2 dimensions:

Get a "pure function" complete integral for u:

Substitute the solution into an expression:

Complete integral that can be expressed using elementary functions:

Complete integral that can be expressed using special functions:

Complete integral for a linear PDE:

Compare with the solution given by DSolve:

Complete integral for a quasi-linear PDE:

Compare with the solution given by DSolve:

Applications  (2)

Find a complete integral of the Clairaut equation:

The complete integral is given by a two-parameter family of planes:

Select a one-parameter family of these planes:

Find the envelope of this one-parameter family of planes:

Verify that the envelope is also a solution:

Visualize the one-parameter family of planes and the envelope solution:

Find a complete integral of the Hamilton–Jacobi equation:

Compute an envelope solution for the equation:

Plot the envelope solution:

Verify that the envelope solution satisfies the equation:

Properties & Relations  (2)

CompleteIntegral finds a complete integral for a nonlinear PDE:

DSolve returns the same solution with a warning message:

Use CompleteIntegral to find a complete integral for a linear PDE:

DSolve returns the general solution for this PDE:

Wolfram Research (2021), CompleteIntegral, Wolfram Language function, https://reference.wolfram.com/language/ref/CompleteIntegral.html.

Text

Wolfram Research (2021), CompleteIntegral, Wolfram Language function, https://reference.wolfram.com/language/ref/CompleteIntegral.html.

CMS

Wolfram Language. 2021. "CompleteIntegral." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CompleteIntegral.html.

APA

Wolfram Language. (2021). CompleteIntegral. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CompleteIntegral.html

BibTeX

@misc{reference.wolfram_2023_completeintegral, author="Wolfram Research", title="{CompleteIntegral}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/CompleteIntegral.html}", note=[Accessed: 16-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2023_completeintegral, organization={Wolfram Research}, title={CompleteIntegral}, year={2021}, url={https://reference.wolfram.com/language/ref/CompleteIntegral.html}, note=[Accessed: 16-April-2024 ]}