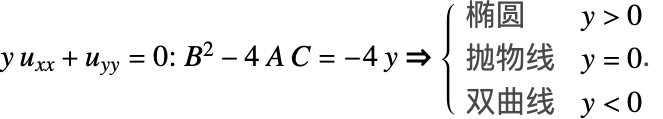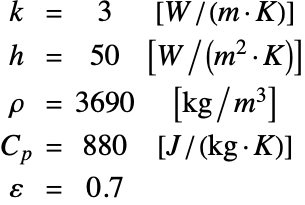引言

流体动力学、电学、电磁学、力学、经典光学或热流中的大多数物理现象都可以用偏微分方程 (PDE) 描述. 事实上，众所周知的物理定律，如麦克斯韦方程、纳维–斯托克斯方程、热方程、波动方程和量子力学的薛定谔方程，都是用偏微分方程表示的；也就是说，这些定律通过关联空间和时间导数来描述物理现象. 这些方程中的导数表示速度、加速度、力、摩擦力、通量和电流等量. 因此，我们希望找到与某个未知量的偏导数相关的方程 [1–3].

PDE 是包含多变量函数的各种偏导数的方程. 与未知函数仅取决于一个变量的常微分方程 (ODE) 不同，未知函数取决于 PDE 中的多个变量. 例如，温度场 可取决于位置 x 和时间 t [2].

在本专题中，为简单起见，将使用以下偏导数的符号约定：

有了这个缩写符号，我们列出一些著名的带单位系数的 PDE [3]：

未知函数 u 被称作因变量，它是多个自变量（如时间 t ）和空间坐标（如 x）的函数. 将因变量 相对于自变量进行微分，所得的项就构成了偏微分方程. 例如，在一维热方程 中，因变量 是两个自变量 x 和 t 的函数，在极坐标的拉普拉斯方程 中，因变量 取决于 r 和 θ [4].

满足 PDE 的函数 称为 PDE [5] 的解，通常是未知和待求解的.

由于一般理论和求解方法通常仅适用于给定的一类方程，因此 PDE 的分类很重要. PDE 的基本分类可以列为 [6]：

1.   PDE 的阶数 . PDE 的 阶数 是方程中偏导数的最高阶数，例如：

2.   变量数 . 变量数即自变量的个数，例如：

两个自变量的最通用的一阶偏微分方程可以写成：

其中 表示其参数的函数，即 中导数的最高阶是 1.

类似地，两个自变量的最通用的二阶偏微分方程可以写成：

3.  系数的类别. 如果方程 (7) 中的 、、、、 和 为常数，则 (8) 被称为常系数 PDE；否则被称为可变系数 PDE [9].

4.  线性. 偏微分方程可以是线性或非线性的. 如果因变量 u 及其所有偏导数在 PDE 中线性出现，则 PDE 是线性的. 更准确地说，两个自变量的二阶线性 PDE 是以下形式的方程：

其中 、、、、、 和 可以是常数或给定的自变量函数，但 、、 不能同时为零 [10].

鉴于这个概念的重要性，让我们再举几个例子：

一般来说，如果对于任何函数 、 和任意常数 ， 是一个满足 和 的微分算子，则 是一个线性微分方程.

考虑已知的偏微分方程 ；可以看到 是线性的，因为：

类似地，对于偏微分方程 ，我们可以看到 是非线性的，因为：

微分算子 的线性导致的一个重要性质是，如果 和 均为解，则 也是解. 这也称为叠加原理.

5.   齐次性 . 如果右侧 完全为零，则方程 ( 11 ) 被称作 齐次的 . 否则，即如果 不完全为零，则方程称为 非齐次的 [ 12 ]. 线性产生的另一个结果是， 作为线性微分算子，如果 的解（齐次解）被添加到 的解（非齐次解），则得到非齐次解 [ 13 ].

在本专题中，我们将按照之前的分类研究 PDE，从最简单的 PDE 开始，由简入难. 对于每个类别，我们将讨论可用于解决这类问题的方法. 请注意，对于尚不存在符号求解方法的 PDE，我们建议使用 NDSolve.

还记得阶数为 m 的线性齐次常微分方程的通解是 m 个独立解和 m 个任意常数的线性组合 [14]. 让我们看看在处理简单的 PDE 情形时，这方面有哪些变化.

范例

最简单的 PDE 是 （其中 ）. 它的通解是 ，其中 是任意单变量函数. 例如 、、 和 都是方程的解. 由于解不依赖于 ，它们在 xy 平面的直线 上是常数，其中 是常数.

对于这个 PDE，DSolve 返回：

下面的 Manipulate 显示，解在 曲线上是常数：

范例

假定我们想要求 的解 . 如果我们对该 PDE 关于 x 积分一次，将得到 ，其中 是任意函数. 由于该 PDE 除了变量 x 还涉及变量 y，积分常数变成 而不是常规的常数系数. 再次对 关于 x 进行积分，得到 . 注意解中有两个任意函数，它们的作用与积分常数在 ODE 中的作用相同 [15].

DSolve 返回此 PDE 的等效的结果：

范例

假设我们想要求 的解 . 事实上，由于关于 y 没有微分，并且在 PDE 中没有显式的 y 出现，这个方程实际上是一个带有额外自变量 y 的常微分方程. 由于 ODE 的通解是 ，使用任意函数 和 而不是 和 作为积分常数，该 PDE 的解为 [16].

对于该 PDE，DSolve 返回相同的结果：

范例

假设我们想要求 的解 . 首先，我们对 PDE 关于 x 进行积分，同时将 y 视为固定值，我们得到 ，其中 是任意函数. 接下来，我们对 关于 y 进行积分，同时将 x 视为固定值，我们得到解 ，其中 和 （使得 ）为任意函数 [17].

DSolve 为这个 PDE 返回相同的结果：

初始和边界条件

正如我们在前面的例子中看到的，PDE 通常有涉及任意函数的解. 为了挑出一个特定的解，需要强加额外的辅助条件. 换句话说，强加条件是为了指定唯一的解. 这些条件根据问题的性质而定，它们作为初始条件和边界条件出现 [18].

初始条件定义时间相关的 PDE 在准确时间 时的物理状态.

例如，对于扩散方程，初始条件为

其中 是一个已知函数，向量 表示空间变量. 对于扩散物质， 是初始浓度，而对于热流体， 是初始温度 [19].

对于波动方程，初始条件成对给出：

其中 是初始位置， 是初始速度. 从物理学角度来看，两个条件缺一不可，以便在后面的时间点唯一地确定位置 [20].

总之，对于 PDE 的每一阶时间导数，必须指定一个初始条件.

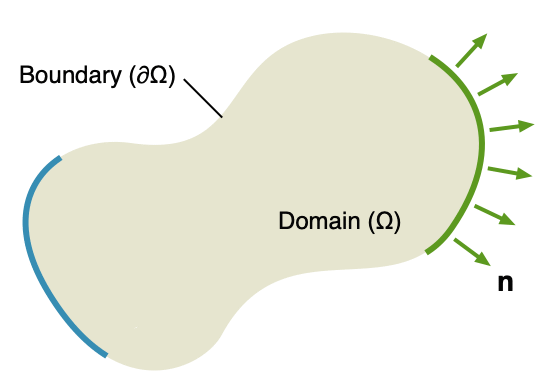
来自实际应用的 PDE 仅在一定的域 Ω 内适用. 例如，对于长度为 l 的振动弦，Ω 为区间 . Ω 的边界，表示为 ∂Ω，仅涉及两个点 和 . 对于鼓面的情形，域是一个平面区域，其边界是围绕该区域的闭合曲线，而对于扩散化学物质，Ω 是容纳液体的容器，因此 ∂Ω 是其边界曲面 [21].

边界条件 是偏微分方程所适用的域 Ω 与该域之外一切从而不是解的一部分的接口. 有必要指定某些边界条件以确定唯一解. 三种最重要和最常见的边界条件类型是：

1.  狄利克雷条件: 在边界 ∂Ω 上指定.

2.  诺伊曼条件: 法向导数e 在边界 ∂Ω 上指定.

3.  罗宾条件: 在边界 ∂Ω 上指定.

在这些条件下，a 可以是 x 和 t 的函数，并且每个条件都应该适用于边界 上的所有 t 和所有 x [22].

请注意，虽然系统函数 NeumannValue 与此处使用的诺依曼（Neumann）或罗宾（Robin）条件之间存在关系，但它们的定义不同.

在图 1 中，可能指定狄利克雷条件的位置在域 Ω 的边界 上以蓝色显示. 狄利克雷条件指定在这些点处满足的解值. 可能指定诺依曼条件的位置在区域 Ω 的边界 上以绿色显示，它们指定边界 上向外法线方向的向内通量.

通常，我们将边界条件写为方程。 例如，诺依曼条件写为方程

其中 g 是已知函数. 如果指定的函数 ，这些边界条件中的任何一个都称为齐次的. 否则，它们被称为非齐次的. 在图 1 中， 表示在 ∂Ω 上的单位法向量，从 Ω 指向外，而 表示 u 在外法线方向上的方向导数[23].

在 Ω 仅是一个区间 的一维问题中，边界仅由两个端点组成，这些边界条件采用简单的形式

其中 、、 和 可以是 t 的函数. 在边界的不同位置可能有不同类型的边界条件[24].

使用初始条件指定的瞬态（时间相关）PDE 称为初值问题 (IVP)，而具有边界条件的 PDE 称为边值问题 (BVP). 涉及初始和边界条件的瞬态偏微分方程称为初值-边值问题 (IVBVP).

范例

假设我们想要求微分方程 的解，其边界条件由 给出，其中 和 .

我们在前面的例子中已经看到，方程 具有通解 . 如果现在施加边界条件 ，我们会发现 ，因此问题的解唯一确定为 .

对于这个 BVP，DSolve 返回：

范例

假设我们想要求解具有常系数的以下问题[25]：

其中 和 .

对于该问题，DSolveValue 返回：

在求解上述问题时，DSolveValue 使用一种通常被称为“Fokas 方法”或“均匀变换方法”的方法. 与求解依赖于变量分离和特定积分变换的常系数线性偏微分方程的经典方法不同，Fokas 变换方法不限于具有特殊边界条件的特定方程. 该方法的细节超出了本专题的范围，我们可以参考 [26] 了解详情.

一阶线性方程—特征方法

具有两个自变量的一般一阶线性 PDE 的初始值问题（IVP）给出如下：

求解一阶线性 PDE 的一种求解技术是特征法，我们的目标是找到自变量 到新变量 的变化，以获得比 (27) 更容易求解的 ODE IVP [28].

在深入细节之前，为了激发方法，假设我们知道问题 (29) 的解. 还假设解 是平滑的，并且我们在 x-t 平面有一条平滑的参数曲线，称之为特征曲线，使得 和 . 这意味着 和 是单个参数 的函数. 现在考虑当我们沿着这些参数曲线移动时，解将如何变化：

请注意，我们可以使用前面关系 (30) 与 (31) 中 PDE 左侧之间的相似性. 如果我们可以找到 和 使得：

(32) 中的 PDE 将约化为 ODE：

因此，根据 的知识，即参数曲线的初始点， 是唯一确定的.

此时我们要回答这个问题：我们如何找到将问题 (33) 约化为 ODE IVP 的特征曲线？

为了找到特性曲线并唯一地求解得到的 ODE (34) ，我们需要定义一个 IVP. 我们要求新坐标 s（用于参数化 x 和 t）和 τ （用于初始曲线）具有以下属性[35]：

1.   沿特征曲线 变化，范围从 0 到 ，从初始曲线开始，在本例中是直线 .

2.   沿初始曲线 变化，并沿每条特征曲线保持恒定.

下图说明了这些属性 [36]：

因此，为了在新变量 s 和 τ 中唯一定义特征曲线，我们定义 IVP：

和

由于 ，当 时，我们有 . 因此在新的坐标系中， 映射到 上. 因此，初始条件 转换为 作为 s 的约化 ODE (37) 的初始条件.

通过应用链式法则和前面的性质，我们得到 ODE IVP：

因此，沿着特性曲线 ，PDE 问题 (38) 被简化为 ODE IVP (39). 一旦我们解决了这个新构造的问题，我们就变回原来的自变量 以获得原始 PDE 问题 (40) 的解 [41].

总之，在这种方法中：

3.  新变量 定义特征曲线 ，每个都以 作为初始点，初始数据沿着这些曲线传播，

4.   s -坐标表示沿特征曲线的点，

5.   -坐标表示已知曲线的初始点 ( )，

6.  对于各个 ，初始值 根据在特征变量中表达 PDE 获得的 ODE，沿着从点 开始的曲线演化，

这称为特征法.

(42) 的特征方程 和 是自治的. 术语“自治”（autonomous） 用于方程对 s 没有显式依赖时.

该特征满足 ODE：

因此对于问题 (43)，特征可以独立于解 u 求解.

方程 (44) 是应用此方法时使用的基本方程，如下例所示.

注意到如果在 (45) 中 ，则 u 沿特征曲线保持不变.

范例：具有常数系数的一阶 PDE

让我们求解常系数方程

其中 a 和 b 为常数且不同时为零. 用 y 替换 t 并使用 (46)，特征曲线满足 ODE . 求解该 ODE 得到：

是特征. 同样， 在每条这样的曲线上保持为常数. 因此 ， 其中 f 为任意函数. 因此，(47) 的通解通过求解 的 获得. 即：

因此

我们直接通过 DSolve 得到了一个等效的解：

我们可以很容易地验证前面的解：

范例：具有可变系数的一阶 PDE

方程

是线性齐次的，但具有可变系数 (y)，其中特征曲线满足 ODE . 求解该 ODE 得到：

是特征. 同样， 在每条这样的曲线上保持为常数. 因此 ，其中 f 为任意函数. 因此，(48) 的通解通过求解 的 获得. 即：

因此

我们直接从 DSolve 得到相同的解：

在几何上，解 的“图片”是它在每条特征曲线上都是常数：

求满足辅助条件 的 (49) 的解. 实际上，将 代入 (50)，我们得到 即 . 因此，. 可以通过 DSolve 得到相同的解：

范例：具有可变系数的一阶 PDE

求解 PDE

特征曲线满足 ODE . 求解该 ODE 得到：

是特征. 同样， 在每条这样的曲线上保持为常数. 因此 ，其中 f 为任意函数. 因此，(51) 的通解通过求解 的 获得. 即：

因此

我们直接从 DSolve 得到相同的解：

范例：具有常数系数的一阶 PDE IVP

假设我们想求解具有常数系数的 IVP [52]：

首先要找到特征曲线，需要求解以下 ODE IVP：

DSolve 给出：

因此，我们的特征曲线是：

使用由 (53) 定义的这个新坐标系，我们将 PDE 简化为 ODE：

求解该 IVP，我们得到：

因此

是 sτ-坐标系中的解. 为了求解作为 x 和 t 的函数的 u，求解变换

以 x 和 t 的形式表示 s 和 τ. 我们有：

因此，我们的答案是

我们可以直接通过 DSolveValue 找到它的等效形式：

如果在三个不同的时间值绘制解，我们得到：

上图以橙色显示初始波 . 请注意，随着时间进展到 和 ，波会减弱； 换句话说，波幅减小. 另请注意，不同时间的峰值略微向右移动.

非线性一阶方程—守恒方程

作为初始范例，我们考虑对交通流的建模问题. 令 表示没有出口或入口坡道的高速公路在点 x 和时间 t 的汽车密度. 然后在高速公路的任何路段 上，u 满足以下等式 [54]：

其中 是通量，即每分钟通过点 x 的汽车. 上述等式的两边代表在路段 内汽车数量的变化.

使用微积分的基本定理，我们得到：

可以重新写作：

因为路段 是任意的，我们得出结论 u 是一维守恒方程的解：

我们现在继续求解守恒方程 IVP：

使用链式法则，我们将 PDE 重写为：

或

其中 .

所以我们要求解的 IVP 是：

与线性情况类似，利用特征方法，特征满足方程：

PDE 简化为 ODE：

且初始条件为

DSolve 告诉我们特征曲线定义为：

且：

关于 u 的 ODE IVP 具有解：

这样，由于

由此得到

且原来的 IVP (55) 有隐式定义的解：

范例

假设我们要解决以下 IVP：

由于 和 ，该 IVP 的隐式解为：

这是由 DSolveValue 找到的解：

虽然在很多情况下我们不能这样做，但在这个特定的例子中，我们可以根据 x 和 t 明确地求解 .

范例

假设我们要求解 PDE：

将方程改写为：

且 ，该 PDE 的隐式解为：

这是由 DSolve 找到的解：

这是对 PDE 的隐式解的验证：

适定性问题

适定性问题指的是一个偏微分方程和一组初始和/或边界条件（或其他辅助条件），其定义域具有以下基本属性 [56]:

1.  存在性，即存在至少一个解 满足所有偏微分方程和条件，并且

2.   唯一性 ，即至多有一个解，并且

3.   稳定性 ，即该唯一解 在数据上连续变化；即如果数据稍微改变，解也会随之稍微改变.

当物理问题由 PDE 建模时，我们期望用物理上现实的辅助条件来构造问题，使问题成为适定的. 在施加的辅助条件太少的情况下，可能存在多个解（非唯一性），该问题称为欠定问题. 但是，如果辅助条件太多，可能根本就没有解（不存在），这个问题就称为超定问题.

范例

为了说明适定 PDE 的概念，请考虑以下设置. 一根受外力振动的弦，其两端按规定的方式移动，满足问题 [57]：

且 . 五个函数 、、、 和 构成了该问题的数据. 存在性和唯一性意味着对于可微函数 f、φ、ψ、g 和 h 存在恰好一个解 . 稳定性意味着，如果这五个函数中的任何一个稍微改变，那么 u 也只会稍微改变.

二阶线性方程的类型

两个自变量的二阶线性方程是以下形式的方程 [58, 59]：

其中 、、、、、 和 可以是常数或 x 和 y 的给定函数.

(60) 中的独立变量 和 通常用于表示空间变量. 对于有时间变量 而不是 的情况，那么我们在 (61) 中就会有项 、 和 . 从分类的角度来看，这没有任何区别； 只是物理意义发生了变化.

形式为 (62) 的二阶线性方程有三种基本类型：

1.  抛物线方程（如果 ，可以化简为规范形式 ，描述热流和扩散过程并满足性质），

2.  双曲线方程（如果 ，可以化简为规范形式 或 ，描述振动系统和波动），

3.  椭圆方程（如果 ，可以化简为规范形式 ，描述稳态现象并满足性质），

其中 表示阶数为 1 或 0 的项. 这将通过以下范例阐明.

范例

热方程

在本节中，我们从一个简单的模型开始考虑热流问题，并在此基础上进一步展开. 我们参考传热模型教程进行一般介绍.

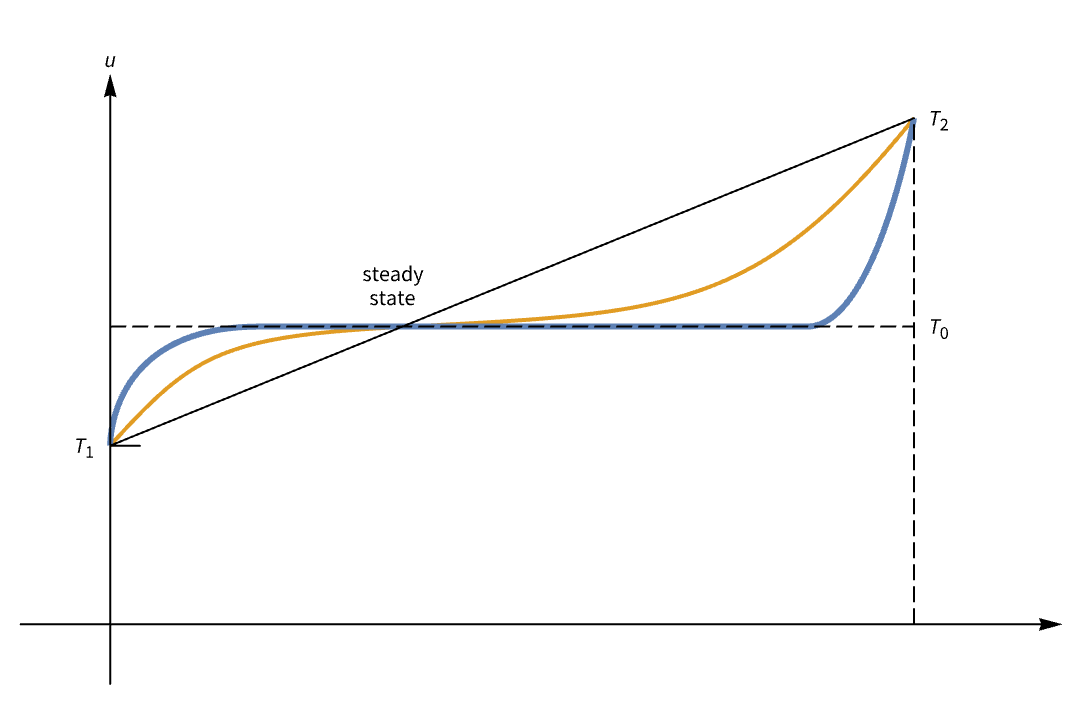
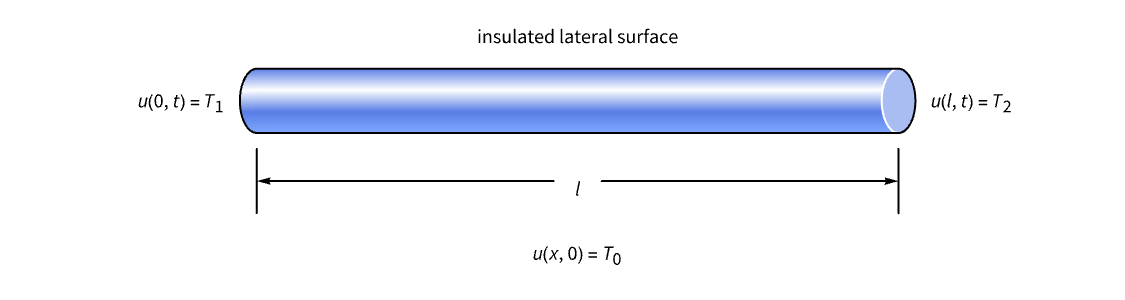
固定末端温度和变量分离

假设我们有一根长度为 l 的导热棒，其表面用绝缘材料包裹，因此热量可以在棒的端部流入和流出，而不会横向穿过边界. 如果将此棒置于温度固定在某个温度 的环境中，经过足够长的时间，整个棒的温度会稳定下来，并达到与环境相似的稳态温度. 然后假设我们在称为 的时刻将棒从环境中取出，并将两个温度分量附加到棒的两端，以将两端分别保持在特定的固定温度 和 . 如果我们监测棒的温度图表，模拟一维热流的基本 PDE 是：

PDE (63) 将两个量 和 关联起来，其中前者表示温度随时间的变化率，后者表示温度曲线 的凹度. 换句话说，PDE (64) 将某一点的温度与相邻点的温度进行比较. 比例常数 k 是制成棒的材料的属性 [65, 66].

由于温度 在所有 的时刻在两个端点 和 处，都固定在 和 ，对于边界条件，我们可以说：

回想一下，我们从棒达到温度 开始监测棒的温度；我们有初始条件：

因此，PDE (67) 、狄里克雷边界条件 (68) 与初始条件 (69) 组成了 IVBVP.

让我们首先假设 ，即棒的两端保持在零温度. 所以，我们要求解热流 IVBVP：

假定 (70) 的解 可以写作：

即解可以分离.

将 (71) 代入 (72) 得到：

将 (73) 的两端同时除以 得到：

其中 必须为常数，因为 仅是 x 的函数，而 仅是 t 的函数.

由方程 (74) 得到两个 ODE：

其通解为

其中 和 为常数.

下一步是将 (75) 施加于 (76)，这要求 . 因此我们有：

由于我们对非平凡解感兴趣，即 和 不应都为零，因此我们得出：

因此，对于 ，

是 (77) 的不同解.

因此 (78) 有无穷多个解，使得：

其中 是常数. 由于线性方程组的叠加原理，解之和也是一个解. 所以，

也是 (79) 和 (80) 的解.

将 (81) 施加于 (82)，我们得到：

上式中， 被称作特征值，而 被称为特征函数.

使用特征函数的正交性，即：

和

我们得到：

将 (83) 代入 (84)，我们得出结论：

这与 DSolveValue 返回的解相同：

上述方法就是所谓的变量分离法，也称为特征函数展开法.

注意 和 的情况不会导致非平凡解，因此我们省略了这些情况.

现在，让我们返回由 PDE (85)、狄里克雷边界条件 (86) 与初始条件 (87) 构成的 IVBVP. 对于该 IVBVP，DSolveValue 返回：

对于 ，，， 和 ，这是解的三维图形：

请注意，在绘制解时，我们在 处截断了无限求和，以便通过使用函数 TruncateSum 获得足够好的求和近似值. 显然，如果在较大的 值处截断可以获得更好的近似值. 在此范例中，在 处截断足以满足我们的目的.

在下一小节中，我们将看到前面解中的前两项构成稳态解.

稳态温度

假设函数 表示温度. 在相同的环境和条件下，经过足够长的时间后，经验表明，温度随时间的变化将逐渐消失. 因此，我们期望随着 t 趋于无穷大， 的极限存在并且仅取决于 x [88]：

并且

稳态温度分布函数 必须满足边界条件 (89) 和热方程 (90)，它们对所有 都有效. 因此， 应该是问题的解：

这等于前面的 IVBVP 的解当 时的极限.

令前面 IVBVP 中的 ，，， 和 ，并用具体值解决问题：

以下 Manipulate 计算表明，经过足够长的时间后，解开始收敛到稳态解：

请注意，计算中的 Quiet 用于抑制计算期间生成的 General::munfl 消息.

绝热棒

现在假设在棒的两端 和 处是绝热的，而不是保持在恒定温度，即给出了诺依曼边界条件. 描述该棒温度的 IVBVP 为 [91]：

对于该 IVBVP，DSolveValue 返回解：

令前面 IVBVP 中的 ， 和 ，用具体数值求解问题：

如果我们在 处截断无限求和，则解的三维图为：

具有热源的非齐次方程

非其次方程

模拟棒在沿棒的任何地方和所有时间 t 都有内部热源的情况 [92]. 使用来自前面范例的相同边界条件 (93) 和初始条件 (94)，在这种情况下 DSolveValue 返回：

令前面 IVBVP 中的 ，，，，，，用具体数值求解问题：

如果我们在 处截断无限求和，则解的三维图为：

如果载有电流的导线通过棒并且电阻产生恒定热源 ，则 DSolveValue 返回 [95]：

令前面 IVBVP 中的 ，，，，，，用具体数值求解问题：

如果我们在 处截断无限求和，则该问题在恒定热源 下解的三维图为：

扩散型问题的边界条件

在本小节中，我们考虑具有边界条件的 IVBVP 范例，这些条件给定为狄利克雷条件、诺依曼条件或罗宾条件.

范例：狄利克雷边界条件

假设对于 的一维棒 (96) 上的热流问题，指定边界上的温度，即两端的条件为狄利克雷条件，初始条件为 [97]:

如果我们在 处截断无限求和，则解的三维图为：

注意到初始条件，：

与边界条件 和 ：

解是满足这些条件的.

范例：诺依曼边界条件

假设对于一维棒 (98) 上的热流问题，其中 和 ，边界处的温度通量已定，即两端条件给定为诺依曼条件，初始条件给定为 [99]：

如果我们在 处截断无限求和，则解的三维图为：

范例：狄利克雷和诺依曼边界条件的混合

假设对于热源在一维棒 (100) 上的热流问题，其中 和 ，指定边界一端的温度和另一端的温度通量，即在一端 的条件作为狄利克雷条件给出，在另一端 作为诺伊曼条件给出. 同时假定初始条件为 ； 那么我们有 [101]：

如果我们在 处截断无限求和，则解的三维图为：

范例：对流问题——狄利克雷和罗宾边界条件的混合

假设对于热源在一维棒 (102) 上的热流问题，其中 和 ，边界一端的温度和另一端周围介质的温度是指定的，即在一端 的条件，作为狄利克雷条件给出，而在另一端 ，作为罗宾条件给出. 在这个问题中， 处杆的末端与具有规定温度 [103] 的周围介质接触. 换句话说，右端受到对流热传递 [104]. 还假设初始条件为 ； 那么我们有：

前面的解是变量分离法的结果，因此无限求和涉及对应于特征值 的特征函数求和. 特征值由条件 [105] 定义：

为了绘制解，我们计算满足 的特征值，以获得解的无限求和的足够好的近似值：

因此有503个特征值满足 .

接下来，让我们计算对应于前 503 个特征值的上述解的总和：

截断解的三维图形为：

范例：诺依曼和罗宾边界条件的混合

假设对于热源在一维棒 (106) 上的热流问题，其中 和 ，一端的温度通量指定，另一端与另一种介质接触，即在一端 的条件，作为诺依曼条件给出，而在另一端 ，作为罗宾条件给出. 还假设初始条件为 ；那么我们有 [107]：

让我们计算满足 的特征值：

因此有504个特征值满足 .

接下来，让我们计算对应于前 504 个特征值的上述解的总和：

截断解的三维图形为：

范例：罗宾边界条件

假设对于热源在一维棒 (108) 上的热流问题，其中 和 ，两端均与另一种介质接触 [109]，即两端的 边界条件均作为罗宾条件给出. 还假设初始条件为 ；那么我们有：

让我们计算满足 的特征值：

因此有504个特征值满足 .

接下来，让我们计算对应于前 504 个特征值的上述解的总和：

截断解的三维图形为：

进入周围介质的热损失

假设一根均匀的棒被两端温度固定的介质包围，并且有热损失通过其侧面到周围介质中. 那么描述这种情况的热流 PDE 是：

其中 项表示通过侧面边界的热损失 [110].

对于 ， 和 ，如果棒的左右两端都保持在固定温度为零，并且初始温度分布为 ，那么我们有以下热流问题：

对于这个 IVBVP，DSolveValue 返回：

例如，如果我们在 处截断无限求和，则解的三维图为：

如果没有具有相同初始条件和边界条件的热损失项，DSolveValue 返回：

要查看热损失项的影响，让我们并排绘出解的图形：

半无限棒中的扩散问题

在前面的所有问题中，我们都是在有限区间上进行研究。 如果考虑的棒很长，我们可以把它当作半无限长，即 ，如果棒是均匀的，且没有外发热源，描述温度的偏微分方程 仍然是 [111, 112]：

假设在 处温度保持不变，即 . 由于没有另一个边界，所以无其他边界条件. 然而，我们期望 在 时仍然是有限的，即有界. 因此我们的模型是：

对于 ， 和 ，DSolveValue 返回：

Assumptions 是 DSolveValue 的选项，在前面的计算中，它用于指定自变量 x 的定义域.

解的三维图形是：

假定在 的边界条件作为诺依曼条件给出：

解的三维图形是：

无限棒中的扩散问题

假设我们要研究一根很长的棒中心的热传导. 在这种情况下，我们可以假设它从 扩展到 . 因此没有边界条件，要解决的问题是 [113]：

对于 和 ，DSolveValue 返回：

解的三维图形是：

假设系统中有一个产生热量的热源：

解的三维图形是：

将复杂的方程转换为较简单的方程

扩散对流方程 [114]：

可以通过使用转换

转换为经过充分研究的热方程

当然，问题中的初始条件和边界条件也必须使用相同的变换进行变换. 假设我们有一个 的 IVBVP，其中初始条件使得 ，两端的狄利克雷边界条件使得 . 对于该 IVBVP，DSolveValue 返回：

如果我们截断无限求和，例如在 处，解的三维图形是：

傅里叶变换和热方程

考虑初始温度 已知的无限棒中的热流，并假设我们要求解 IVP：

这也称为柯西问题 [115].

首先，令 ，并转换方程：

然后转换初始条件，：

因此，我们在 中有一个带有初始条件的 ODE. 求解该 ODE-IVP，我们得到：

现在，将上解转换回原始 PDE-IVP 的解：

对该解应用 ExpToTrig 并化简，得到：

可以通过 DSolveValue 直接找到相同的解：

解的三维图形是：

拉普拉斯变换和热方程

想象一个长度为 的圆柱杆，其弯曲的侧面完全绝缘，因此没有热量可以进入或逸出. 在时间 时，杆的温度由 给出，其中 . 对于 ，杆两端的温度分别为 和 . 杆中温度 的 IVBVP 为 [116]：

首先，令 ，使用 LaplaceTransform 将偏微分方程转换为常微分方程：

注意到初始条件 用于前面的 ReplaceAll.

转换边界条件给出：

求解 ODE-IVP 给出：

现在，转换前面的解得到原始 IVBVP 的解：

直接使用 DSolveValue 可以得到相同的解：

解的三维图形是：

二维热方程

我们现在研究一个矩形薄板在 和 的有限二维域上的温度分 ，其中板的侧面是绝缘的 ，因此侧面没有热量损失. 边界 和 保持在固定的零温度（狄利克雷条件）. 边界 是绝缘的（诺伊曼条件），边界 与温度为零的周围介质接触（罗宾条件）. 该系统没有产生热量的热源. 初始温度分布为 ，薄板材料的恒定热导率为 . 因此，我们要求解的 IVBVP 是 [117]：

对于该 IVBVP，DSolveValue 得到解：

我们来计算特征值，使得 ：

所以有 100 个特征值使得 .

接下来，让我们计算对应于前 100 个特征值的上述解的总和：

现在我们可视化解的三维图：

三维热方程

我们再来研究一个长方体固体中的温度分布 ，其中 ， 和 . 边界 、、 和 保持在零度的固定温度. 边界 是绝缘的，边界 与温度为零的周围介质接触. 该系统没有产生热量的热源. 初始温度分布为 ，固体材料的恒定热导率 . 因此，我们要求解的 IVBVP 是 [118]：

对于该 IVBVP，DSolveValue 得到解：

让我们计算特征值，使得 ：

所以有 202 个特征值，使得 .

接下来，让我们计算与前 202 个特征值对应的上述解中的总和，并在例如 处截断无限和：

时解的三维等高线图：

极坐标和圆柱坐标中的热流 IVBVP

在本小节中，我们研究圆形区域和圆柱形区域中的热流 IVBVP. 在圆形区域，我们首先考虑圆形对称的情况，即无角度依赖性. 在第二个例子中，我们考虑角度依赖的情况. 第三个范例处理圆柱域中的热流方程.

圆对称薄圆板中的热传导

假设我们研究半径为 r 的薄圆板中的热传导. 并假设系统是圆对称的，热系数在空间上是不变的，并且没有热源. 那么我们处理的 PDE 即 [119]：

假设我们要求这个偏微分方程在有限区间 上的解；然后我们需要 即 ∃_M 的边界满足 ≤M, ∀_tt>0. 当 时，假定我们有下列边界条件：

及以下初始条件：

DSolveValue 返回该 IVBVP 的下列解：

该解的三维图形为：

解在圆形区域 中的三维图形为：

非圆对称薄圆板中的温度分布

假设我们研究一个半径为 r 的薄圆板在二维区域 和 上的温度分布 ，无发热源. 假设圆板很薄，因此忽略 z 相关性，我们处理的 PDE 为 [120]：

其中一个边界条件是要求 的边界. 当 时，假定我们有以下边界条件：

和以下初始条件：

DSolveValue 返回该 IVBVP 的下解：

出于实际目的，我们应该在前面的解中设置 . 因此我们需要计算 ， 时的前 50 个特征值 ：

现在使用这 50 个特征值计算总和：

可视化解的三维图形：

现在我们在圆柱域中可视化解的三维图形：

具有角周期性的圆柱体中的温度分布

假设我们研究一个半径为 r 的圆柱体在三维区域 、 和 上的温度分布 . 因此，我们正在处理的 PDE 是 [121]:

边界条件之一是 的有界性. 在 的情况下，假设我们有以下边界条件：

且有下列初始条件：

DSolveValue 返回该 IVBVP 的以下解：

出于实际目的，我们应该截断无限求和，例如在 处：

我们可视化 时解的三维等高线图：

波动方程

在本节中，我们从一个简单的问题开始考虑波动问题，并在此基础上进一步拓展. 我们参考波动方程教程进行一般介绍.

一维波动方程

假定我们考虑长度为 l 的弦的微小振动. 假设弦的每一端都固定，弦的振动发生在一个平面内，即位移平行于弦. 如果我们从平衡状态监测弦的纵向位移（用 表示），则模拟弦的纵向和扭转振动的基本 PDE 是波动方程是 [122]：

其中 c 是与材料 [123] 的线性密度相关的常数物理参数，也称为波速 [124]. 项 表示由于弦的张力而产生的净力. 波动方程包含一个二阶时间导数 ，因此要唯一定义 的解，它需要两个初始条件初始条件：

这与热方程问题的情况不同，后者只需要一个初始条件 [125].

范例：振动弦

例如，假设我们有一个长度为 1 且 的弦； 那么以下 PDE、边界条件和初始条件构成 IVBVP：

DSolveValue 对此返回：

如果我们截断无限求和，例如在 处，则 x 的各种解值的二维图如下：

达朗贝尔（D'Alembert ）解

在某些情况下，可以直接根据初始数据阐明波动方程 (126) 的解. 令 ， 且 . 则波动方程 (127) 变为 [128]：

DSolve 对这个新的 PDE 返回以下解：

因此，如果我们现在转换回原始变量，则波动方程 (129) 的解为：

DSolveValue 可以直接找到解的等价形式：

接下来，如果对无限长的弦上的波动方程施加初始条件并求解，我们会根据初始数据得到解：

该解称为达朗贝尔解或行波解，将解表示为两个波的叠加，一个向左移动，另一个向右移动，传播速度为 c. 这种形式的解显示了初始数据如何影响以后的解 [130].

一维波动方程的推广：电报方程

这次假设我们的模型有阻尼效应以及作用在系统上的外力. 还假设我们有一个与弦的位移相反的复原力. 因此，对波动现象建模的 PDE 变为：

其中 表示与空间时间相关的波幅，c 表示波速，β 表示复原力系数，γ 表示介质的阻尼系数， 表示外力. PDE (131) 也称为电报方程. 假设介质是均匀的，前面所有的系数都是空间不变的，可以写成常数 [132, 133].

假定

则 DSolveValue 返回：

如果我们在例如 处截断无限求和，则解的三维图形为：

非均匀边界条件

我们来考虑一个在边界处给出热源的问题，即给出不均匀的边界条件. 因此，假设我们有一个 IVBVP，例如 [134]:

对于此 IVBVP，DSolveValue 返回：

截断无限求和，例如在 处，得到：

截断解的三维图是：

无界区域中的波动方程

在本小节中，我们考虑在射线和直线上的波动现象问题.

范例：射线上的波动方程

考虑该问题：

在射线 上，则 DSolveValue 返回 [135]：

解的三维图如下：

范例：直线上的波动方程

考虑该问题：

在直线 上，则 DSolveValue 返回 [136]：

解的三维图如下：

范例：具有热源的直线上的非齐次波动方程

考虑非齐次 IVP：

在直线 上，则 DSolveValue 返回 [137]：

让我们列出要在 ListPlot 中使用解的数据点：

使用 ListPlot，我们得到以下三维图：

与波动方程相关的边界条件

在本小节中，我们考虑带有狄利克雷、诺依曼和罗宾边界条件的波动现象 IVBVP.

范例：边界上的狄利克雷条件

假设对于有限弦上的振动问题，我们有受控端点，即两端的条件作为狄利克雷条件 [138]：

如果截断无限求和，例如在 处，则解的三维图为：

范例：边界上的诺依曼条件

假设一个有限弦上的振动问题，在边界上指定力，使得弦的末端可以在无摩擦套筒上垂直滑动，即两端的条件作为 诺依曼条件给出 [139]：

如果截断无限求和，例如在 处，则解的三维图为：

范例：边界上狄利克雷和诺依曼条件的混合

假设对于有限弦上的振动问题，有一个受控端，并且在另一端指定了一个力，即一端的条件为狄利克雷条件，另一端的条件为诺依曼条件 [140]：

如果截断无限求和，例如在 处，则解的三维图为：

范例：边界上狄利克雷和罗宾条件的混合

假设对于有限弦上的振动问题，我们有一个受控端，在另一端有一个弹性附件，即一端的条件为狄利克雷条件，另一端的条件为罗宾条件 [141]：

让我们计算特征值，使得 ：

因此有 202 个满足 的特征值.

接下来，让我们计算上述解中对应于前 202 个特征值的解的总和：

截断解的三维图是：

范例：边界上的罗宾条件

假设对于有限弦上的振动问题，在两端都有弹性附件，即两端的条件作为罗宾条件给出 [142]：

计算满足 的特征值：

所以有 403 个特征值满足 .

接下来，让我们计算上述解中与前 403 个特征值对应的解的总和：

截断解的三维图为：

傅里叶变换和波动方程

假设我们要求解以下描述无限长弦 [143] 振动的 IVP：

首先，令 并变换方程：

再转换初始条件：

这样我们就得到了在 中带有初始条件的 ODE. 求解该 ODE-IVP，得到：

现在，将前面的解转换回原始 PDE-IVP 的解：

将 ExpToTrig 应用于此解并进行化简：

直接使用 DSolveValue 可以得到同样的解：

解的三维图为：

拉普拉斯变换和波动方程

假设我们要求解以下描述振动 [144] 的 IVBVP：

首先，令 ，使用 LaplaceTransform 将 PDE 转换为 ODE：

注意到初始条件， 和 ，用于前面的 ReplaceAll 中.

转换边界条件得到：

求解 ODE-IVP 得到：

现在，将先前的解转换回来得到原始 IVBVP 的解：

直接使用 DSolveValue 可以得到同样的解：

解的三维图为：

二维波动方程

假设我们研究在 和 的有限二维矩形域上矩形薄膜中的横向振动. 假设薄膜处于无阻尼的介质中. 同时假设边界是固定的，并且薄膜的初始位移为 ，初始速度为 . 系统无外力作用，波速为 . 因此，我们想要求解的表示横波振幅 的 IVBVP 为 [145, 146]：

对于此 IVBVP，DSolveValue 得到的解如下：

让我们截断无限求和，例如在 处：

现在，我们将解的三维图可视化为：

三维波动方程

假设我们研究在 、 及 上的长方体中的振动. 我们假设介质中没有阻尼. 同时假设边界是固定的，物体的初始位移为 和初始速度为 . 系统不受外力作用，波速 . 我们寻求波幅 . 因此，我们要解决的 IVBVP 是 [147, 148]：

对于此 IVBVP，DSolveValue 得到的解如下：

让我们截断无限求和，例如在 处.

对于 ：

解的三维等高线图为：

圆形膜的对称振动

我们来研究半径为 a 且边缘固定的圆形薄膜位移问题. 首先处理初始条件独立于 θ 的简单情况. 波动方程 [149]：

定义位移，在极坐标下变为：

在极坐标中.

假设 是有界的，在半径为 1 的圆形薄膜中求解以下 IVBVP：

如果截断无限求和，例如在 处，则解的三维图为：

振动鼓头

假设我们要研究半径为 a 的圆形鼓膜 的振动. 则二维波动方程 [150]：

变为：

在极坐标中，.

假定 有界，让我们在半径为 2 的圆鼓中求解以下 IVBVP：

如果截断解中的无限求和，例如在 处，我们得到：

现在我们可视化解的三维图：

将 中解的三维图可视化为：

具有角周期性的圆膜的振动

对于下面的初值和边值问题，我们考虑具有角周期性的圆形膜的振动，假设 有界，则 DSolveValue 返回 [151]：

出于实际目的，我们在前面的解中截断无限求和，例如在 处. 因此，我们需要计算 和 的前 50 个特征值 ：

现在使用这 50 个特征值计算总和：

我们将解的三维图可视化为：

我们将 中解的三维图可视化为：

势能或拉普拉斯方程

二维稳态温度分布的拉普拉斯方程为

方程 (152) 也表达了二维膜的与时间无关的平衡状态，因此它是二维热方程和波动方程的重要共同部分. 函数的拉普拉斯算子告诉我们函数在某一点的值与其在相邻点的平均值的偏差. 例如，稳态、拉伸的静止橡胶膜满足拉普拉斯方程，因此膜在任何点的高度等于膜在附近点 [153, 154] 的平均高度.

泊松方程是 =f，其中 f 是空间变量的函数，并描述了几种物理现象，例如 [155]：

类似地，三维拉普拉斯方程为：

矩形中的势能

矩形中的狄利克雷问题是数学物理中重要的基本问题之一. 假设我们想研究无电荷矩形域 [156] 中的静电势：

对于此 BVP，DSolveValue 返回：

如果我们截断无限求和，例如在 处，则解的三维图形为：

更多矩形中的势能 BVP 范例

在本小节中，我们考虑边界条件为狄利克雷条件、诺依曼条件或罗宾条件的 BVP 范例.

范例：边界上狄利克雷条件和诺依曼条件的混合

假设边界条件同时涉及狄利克雷条件和诺依曼条件 [157]：

如果我们截断无限求和，例如在 处，则解的三维图形为：

范例：边界上狄利克雷、诺依曼和罗宾条件的混合

假设边界条件同时涉及狄利克雷、诺依曼和罗宾条件 [158]:

出于实际目的，我们在前面的解决方案中截断无穷求和，例如在 处. 因此我们需要计算 的前 200 个特征值 ：

现在使用这 200 个特征值计算总和：

截断解的三维图形是：

无限区域的势能

在本小节中，我们考虑了上半平面、右半平面、无限条带、半无限垂直条带和半无限水平条带的势能问题.

范例：上半平面上的势能

假设 在无限半平面上是绝对可积的，并考虑上半平面上的稳态温度分布. 因此 BVP 为 [159]：

对此 DSolveValue 返回：

解的三维图形为：

范例：右半平面上的势能

假设 在无限半平面上是绝对可积的，并考虑右半平面上的稳态温度分布. 因此 BVP 为 [160]：

对此 DSolveValue 返回：

解的三维图形为：

范例：沿无限条带的势能

假设 在无限薄板上是绝对可积的，并考虑侧面绝缘的薄板上的稳态温度分布. 因此 BVP 为 [161]：

对此 DSolveValue 返回：

让我们使用 NIntegrate 计算解的数据点列表：

现在使用 ListPlot3D 的解的三维图形是：

范例：沿半无限垂直条带的势能

假设 在半无限条带上是绝对可积的，并考虑在这个半无限垂直带上的稳态温度分布. 因此 BVP 为 [162]：

对此 DSolveValue 返回：

对于 的解的三维图形是：

对于 的解的三维图形是：

范例：沿半无限水平条带的势能

假设 在半无限条带上是绝对可积的，并考虑在这个半无限水平带上的稳态温度分布. 因此 BVP 为 [163]：

对此 DSolveValue 返回：

对于 ，解的三维图形是：

对于 ，解的三维图形是：

非均匀边界条件

我们来考虑在边界 [164] 处作用的源的问题：

对于这个具有不均匀边界条件的 BVP，DSolveValue 返回：

如果我们在例如 处截断无限求和，则解的三维图形为：

极坐标中的拉普拉斯方程

在本小节中，我们考虑极坐标中的势能 BVP 问题.

圆的内狄利克雷问题

假设我们要解决描述圆内静电势的内部狄利克雷问题，当在边界上给出电势 [165] 时：

对于此 BVP，DSolveValue 返回：

解的三维图形是：

圆形区域 上解的三维图形为：

环形中的狄利克雷问题

假设我们要求解两个圆之间（即一个环形空间中）的内部狄利克雷问题，当在边界上给出电势 [166] 时：

对于此 BVP，DSolveValue 返回：

解的三维图形是：

圆形区域 中解的三维图形为：

具有周期性边界条件的薄板中的电势

假设原点处的温度有限，我们来研究具有绝缘侧表面和周期性边界条件 [167] 的圆柱域上薄板的稳态温度分布：

解的三维图形是：

圆形区域 中解的三维图形为：

圆盘上的电势

假设原点处的温度有限，我们来研究具有绝缘侧表面 [168] 的圆柱域上薄板中的稳态温度分布：

解的三维图形为：

圆形区域 中解的三维图形为：

圆内的非齐次狄利克雷问题

假设我们想求一个圆盘中的势能，以响应作用在圆盘内的强迫项 . 因此，我们在半径为 a 的圆盘上有一个具有非齐次边界条件的非齐次拉普拉斯 PDE-BVP，DSolveValue 返回 [169]：

如果 ， 且 ，我们有：

解的三维图形为：

圆形区域 中解的三维图形为：

球坐标中的拉普拉斯方程

在本小节中，我们考虑球坐标中的势能 BVP.

各自处于恒定势能的两个球体之间的势能

假设我们想要求两个保持在不同温度 [170] 的球体之间的稳态温度：

对于此 BVP，DSolveValue 返回：

对于 ，， 和 ，我们有：

球体内部的狄利克雷问题

当温度（仅取决于 θ）在边界 [171] 上指定时，假设我们想求此时球体内的稳态温度：

对于此 BVP，DSolveValue 返回：

对于 和 ，我们有：

三维拉普拉斯问题

我们考虑在一个长方体 [172] 中的拉普拉斯问题：

如果我们在例如 处截断无限求和，则解的三维等高线图为：

非线性偏微分方程

由于叠加原理不适用于非线性方程，因此不能应用特征函数法和变换法，处理非线性问题有许多其他方法.

激波和稀疏波解决方案

初始数据由两个常数状态 和 组成并在 处具有跳跃不连续性的 IVP 称为黎曼问题 . 现在让我们考虑带有黎曼问题 [173, 174] 的伯格斯方程：

其中初始条件以下式给出：

对于 ，特征相交，因此无法构造平滑解. 相反，我们可以构造一个以 Rankine–Huguenot 条件确定的速度移动的冲击波形式的弱解. 对于 ，我们可以根据简单波原理构造一个稀疏扇（超音速稀疏）形式的弱解：

因此当 u(x,0)= 时，我们得到激波解：

其解的三维图形为：

而当 u(x,0)= 时，我们有一个稀疏扇形解：

其解的三维图形为：

范例：广义伯格斯方程

考虑湍流理论中的广义粘性伯格斯方程 [175]：

其中初始条件以下式给出：

对于此 IVBVP，DSolveValue 返回：

对于 ϵ 的任何正值，该解都是平滑的：

当 ϵ 接近 0 时，该解在极限处产生冲击不连续：

Charpit 方法

假设我们有 的一阶偏微分阶，形式为 [176]：

其中 ，. 我们的目标是找到另一个与方程 (177) 具有相同解的方程，形式为 ，其中 是一个常数. 然后思路是结合这两个方程并求解 p 和 q，然后求解 Pfaffian微分方程的 u：

和 的解相同并且 (178) 可积，这两个要求导致了相容条件：

条件 (179) 导致特征方程（Charpit 方程）：

如果我们可以得到 (180) 关于 p 或 q 或两者的积分，则可以将该积分作为附加微分方程，即 ，我们可以求解：

得到 p 和 q 以使得 (181) 可积. 对 (182) 积分得到 (183) 的解.

注意，求解 Pfaffian 微分方程 (184) 会得到 (185) 的完全积分. 函数 CompleteIntegral 直接返回一阶 PDE 的完全积分.

范例

假设我们有以下非线性微分方程：

则根据 (186)，我们有

使用 (187) 中的等式，我们得到：

用 (188) 的结论求解 (189) 得到 u，提供了我们所求的解：

DSolve 对此 PDE 给出相同的解，与 (190) 一致：

CompleteIntegral 给出相同的完全积分：

雅可比方法

假设我们有 的一阶偏微分阶，形式为 [191]：

其中 ， 及 . 我们的目标是找到与方程 (192) 具有相同解的另外两个方程，形式为 和 . 那么思路就是结合这三个方程，求解 、 和 ，然后求解关于 u 的 Pfaffian 微分方程：

和 的解应该与 (193) 的解相同，这导致相容条件：

其中 是泊松括号.

条件 (194) 导致特征方程：

如果能得到 (195) 的积分，即 和 ，然后验证 ，我们可以求解：

得到 、 和 ，这将使得 (196) 可积. 对 (197) 积分得到 (198) 的解.

该方法适用于具有三个或更多自变量的一阶偏微分方程.

与 Charpit 方法相似，求解 Pfaffian 微分方程 (199) 导致 (200) 的完全积分，这可以直接由 CompleteIntegral 计算.

范例

假设我们有以下非线性微分方程：

因此根据 (201) 我们有：

注意 . 求解 (202) 和 (203) 得到 ， 和 ：

利用 (204) 的结论，Pfaffian 微分方程 (205) 变为：

对 (206) 积分给出：

DSolve 对此 PDE 给出相同的解，与 (207) 一致：

CompleteIntegral 给出相同的完全积分：

行波解

在移动的参考系 中，通过让新的自变量比如 ，可以将 的多项式偏微分方程转换为新自变量 的常微分方程. 由于 的导数是 的多项式，即 ，因此所有导数 的多项式都是 的多项式. 因此，使用链式法则，将多项式偏微分方程转换为 的常微分方程，它有 的多项式系数. 然后我们可以求常微分方程的多项式解，从而生成一个所有解的子集. 该结论可以推广到涵盖其他双曲三角函数 [208] 的解.

范例：科特韦赫-德弗里斯方程（KdV）方程

普遍存在的 KdV 方程：

模拟运河中的浅水波和等离子体 [209] 中的离子声波：

假设存在初始条件和边界条件：

这是解的图形的可视化：

范例：博欣内斯克（Boussinesq）方程

具有实数参数 的经典博欣内斯克方程，

由博欣内斯克提出，描述水平尺度远大于水深的地表水波 [210]：

假设对于 存在初始条件和边界条件：

这是解的图形的可视化：

范例：卡东穆塞夫-彼得韦亚斯维利（KP）方程

卡东穆塞夫-彼得韦亚斯维利（KP）方程是在两个空间坐标和一个时间坐标中的非线性偏微分方程，它模拟缓慢依赖于横坐标 [211] 的小振幅非线性长波的演变：

的情况称为 KPII 方程和模型，例如具有小表面张力的水波. 的情况称为 KPI 方程，可用于模拟具有高表面张力的薄膜中的波.

KP 方程被视为二维空间上的通用可积方程，就像 KdV 方程被视为单空间维度上的通用可积方程一样. KP 方程通常写成与其 Lax 对的相容形式的系统：

对此 DSolve 返回：

假定对于 KPII（即 ），我们有初始条件和边界条件：

这是解的三维图形的可视化：

范例：KdV–Zakharov–Kuznetsov (KdV-ZK) 方程：

KdV–ZK 方程 [212]，

模拟磁化多组分等离子体中的离子声波，包括负离子：

假设对于 存在初始条件和边界条件：

应用

在本节中，我们考虑将 PDE-IVBVP 应用于物理、工程、金融等领域的问题.

振动梁（四阶 PDE）

与小提琴弦的横向振动相反，细梁的横向振动表现出对弯曲的抵抗力，这种抵抗力将波动方程变为四阶梁方程：

其中 是刚度常数与梁 [213] 的线密度之比.

考虑一个细梁的微小振动，如果它的末端保持静止，但端点处的斜坡可以移动，则由 表示的梁的弯矩在端点处应该为零. 那么我们应该有以下初始条件和边界条件 [214]：

范例：

假设我们有一个长度为 1 且 的梁；则以下偏微分方程、初始条件和边界条件构成 IVBVP：

对此 DSolveValue 返回：

解的三维图形为：

布莱克-舒尔斯方程

当标的资产价格为风险中性时，所有欧式期权都满足布莱克-舒尔斯偏微分方程. 如果 是标的资产 和经过时间 、无风险利率 、股息收益率 与资产价格的波动率或年化标准差 的期权价值，则模拟所有欧式期权的方程为 [215]：

如果 是履约价， 是到期时间，则看跌期权的初始条件为 [216]：

对于看跌期权问题，DSolveValue 返回：

对于看跌期权，隐含的边界条件为：

计算参数典型值的期权值：

与 FinancialDerivative 给出的值比较：

看涨期权的初始条件为 [217]：

对于看涨期权问题，DSolveValue 返回：

对于看涨期权，隐含的边界条件为：

计算参数典型值的期权值：

与 FinancialDerivative 给出的值比较：

薛定谔方程

在量子力学中，质量为 m 的自由粒子的运动由时间相关的自由薛定谔方程描述：

其中 是普朗克常数除以 ，u 是描述粒子 [218] 运动的波函数.

然后对于以下 IVBVP，DSolveValue 返回：

假定 ，解的三维图形如下：

球面谐波

假设我们想要求当边界上的势能为 时，半径为 3 的球体内的势能. 为此，我们必须在没有方位角对称 [219] 的球体中求解拉普拉斯 PDE-BVP：

让我们定义截断的解：

注意，在较大的 值处截断总和也给出相同的解：

这是解的球形三维图形的可视化：

偏微分方程组

许多物理系统不能用单个偏微分方程来描述，而实际上是由偏微分方程组来建模的. 在这些方程中，压力、密度和温度等未知函数及其偏导数由物理定律描述，我们的目标是同时找到所有这些函数 [220].

研究偏微分方程组的另一个原因是，通常可以将单个高阶偏微分方程写为一阶偏微分方程组 [221].

范例：具有常系数的系统

对于具有常系数的偏微分方程组的以下 IVBVP，DSolve 返回：

当 和 时，我们有：

这是 的三维图形：

这是 的三维图形：

范例：具有可变系数的非齐次系统

对于具有可变系数的非齐次偏微分方程组的以下 IVBVP，DSolveValue 返回：

这是 的三维图形：

这是 的三维图形：

建模

热力学工程中的传热对能量传输的建模很有用. 让我们求解一个稍微修改的基本传热范例：

宽度 和高度 的模型域 Ω 是嵌入高导热材料中的陶瓷条. 陶瓷条的侧边界保持在恒定温度 . 顶面通过热对流散热，省略 时对周围环境的热辐射. 然而，假设底部边界是绝热的.

我们的目标是求陶瓷条的稳态温度分布.

设置一个宽度为 、高度为 的矩形域.

陶瓷条的热导率 k、传热系数 h、密度 ρ、热容 和发射率 ε 由以下各式给出：

定义模型参数：

在左右边界处设置温度表面边界条件：

设置上表面的对流边界条件：

默认的隔热边界条件隐式应用于剩余的底部边界：

用 NDSolveValue 和 DSolveValue 求解传热 PDE 模型：

可视化稳态温度分布：

总结

本教程概述了偏微分方程（PDE）、初值边值问题（IVBVP）和 DSolve 和 DSolveValue 中可用于解决这些问题的方法.

References

1.  Strauss, W. Partial Differential Equations: An Introduction. (2nd ed.) John Wiley & Sons, Inc., 2008.

2.  Farlow, S. J. Partial Differential Equations for Scientists and Engineers. Dover Publications, Inc., 1993.

3.  Powers, D. L. Boundary Value Problems and Partial Differential Equations. (6th ed.), 2010.

4.  Trim, D. W. Introduction to Complex Analysis and Its Application. (1st ed.) PWS Pub. Co., 1996.

5.  Evans, L. C. Partial Differential Equations. (2nd ed.) American Mathematical Society, 2010.

6.  Zwillinger, D. Handbook of Differential Equations. (3rd ed.) Academic Press, 1997.

7.  Baldwin, D., Göktaş Ü., Hereman W., Hong L., Martino R. S. and Miller J. C. "Symbolic Computation of Exact Solutions Expressible in Hyperbolic and Elliptic Functions for Nonlinear PDEs." Journal of Symbolic Computation 37, no. 6 (2004): 669–705.

8.  Kelly, M. "Evaluation of Financial Options Using Radial Basis Functions in Mathematica." The Mathematica Journal 11, no. 3 (2010): 333–257.

9.  Deconinck, B., Drogdon T. and Vasan V. "The Method of Fokas for Solving Linear Partial Differential Equations." SIAM Review 56 (2014): 159–186.

10.  Stavroulakis I. P. and Tersian S. A. Partial Differential Equations—An Introduction with Mathematica and Maple. (2nd ed.) World Scientific Pub. Co. Re. Ltd., 1999.