書式 expr/.rules を使い複数の規則を適用すると，各規則は式 expr の各部分に代る代る試される．ある規則が適用されると直ちに，それに対応した変換が施され，変形された該当部分が返される．

expr/.rules による変換操作では，各規則は式 expr の各部分に一度だけ試される．

ときには，式に変化がなくなるまで，繰返し規則を適用しなければならないことがある．これを行うには，書式 expr//.rules による繰返し置換操作，または，組込み関数ReplaceRepeated[expr,rules]を使う．

//.（「スラッシュ・スラッシュ・ドット」と読む）が使われると，Wolfram言語は式を繰り返し操作しながら与えられた各規則を適用していく．この操作は，全く同じ結果が続けて得られるまで繰り返される．

循環してしまうような規則の組合せを与えると，いつまでたっても//.の置換操作が終らなくなってしまう．実際には，//.による特定の式に対して繰り返される操作の最大回数は，オプションMaxIterationsの現行値で決定される．繰返しを何回でもできるようにしたければ，ReplaceRepeated[expr,rules,MaxIterations->Infinity]を使う．そうした場合でも，Wolfram言語を手動で中断すれば操作をいつでも停止することができる．

2つの置換演算子/.と//.は，ともに，式の各部分に対して各規則を試行していく，という同じ機能を持つ．これに対して，Replace[expr,rules]は，式 expr 全体に対して規則を適用するが，式の各部分には適用しない．

それでも，ReplaceをMapやMapAt等の他の関数と組み合せて使うことで，置換の対象になる式の部分を確実に限定することができる．また，別の節ですでに触れたが，関数ReplacePart[expr,new,pos]でも，指定されたオブジェクトによる式の部分的置換を行うことができる．

他のシンボル式と同じように変換規則のリストにも各種の操作処理を施すことができる．規則からなるリストにはよく参照名が割り当てられる．

リスト形式で規則を与えることで数学的関係やその他の関係を表すことができる．その際は，リストに名前を付けておき，実際に使うときには，ほしいリストを名前で簡単に指定できるようにしておくとよい．

ほとんどの場合は，リスト中の1つの規則だけが実際の式に適用される．ただし，演算子/.は，リストにある全規則を1つずつ判定していくので，リストの規則が多ければ多いほど処理に時間がかかる．

効率よく/.が進むように，規則のリストに前処理を施すことができるようになっている．これを行うには，関数Dispatchを規則のリスト全体に作用させる．結果として，「呼出し表」を含んだ規則のリストを表したオブジェクトを得ることができる．この表は，/.による適用可能な規則を即座に「呼び出す」ための情報を備え，これを参照することで，全規則を代る代るに判定する必要がなくなる．

たくさんの規則を持つ長いリストでは，呼出し表を設けることで，置換操作をより早く済ませられる．パターンオブジェクトを含まない単体のシンボルやその他の式に関した規則を与える場合には，この方法を使うと特に効果的である．呼出し表を作っておくことで，演算子/.による処理は，与えられた規則がいくつあってもほとんど同じ時間しかかからなくなる．逆に，呼出し表を使わない場合は，/.では規則の総数に正比例しただけの時間がかかってしまう．

置換演算子/.を使うことで，特定の式に変換規則を適用することができる．それでは，変換規則を必要なときに自動的に適用させるにはどうしたらよいだろう．

これを行うには，Wolfram言語式やパターンに対して特定値の割当てを行う．各割当ては，特定された形の式が現れるたびに適用される変換規則を指定する．

ModuleやBlock等の構成体の内部にない限り，すべての割当て操作は現行セッションにおいて継続する．故意に取り去られるか，別の値で上書きされるまでは有効なまま残る．

その継続性のため，割当て操作は気を付けて行う．Wolfram言語を使うときに最もよく見受けられる誤りは，変数x等に割当てを前に定義したことを忘れてしまい，xを再び使ってしまうというものである．

この程度の間違いは次のようにすれば未然に防げる．第1に，なるべく恒久的な割当ては行わない．置換演算子/.等の，より限定された構成体を使うようにする．第2に，割当てを行ったなら，使う必要がなくなり次第に割当ての取消し演算子=.またはClearを使い割当て関係を解除しておく．

もうひとつの予防策として，よく使われそうな名前や簡単な名前の付いた変数に割り当てるときは十分に先の事を考えてから行うようにする．xのような名前はシンボルとしてよく使われるだろう．x=3等の割当てを行ってしまうと，xは現れるたびに3に置換され，シンボル的なパラメータとしては使えなくなってしまう．

通常，後で別の用途を想定しているような変数には恒久的な値は割り当てない方がよい．例えば，光の速度を定数化する意味で変数cに3.*10^8の値を割り当てたとする．後でcを別の用途，例えば，単なる未確定係数として使おうとしてもそれができなくなってしまう．そうしないためには，cの代りにSpeedOfLightというようにできるだけ特定化された名前を使う．

特に手続き的なプログラムを書いているときは，特定の変数に割り当てられた値をいろいろと変えていく必要が出てくる．これは，新たな値を構築し，x=value のような割当てを明示的に行うことでもできるが，変数の値の加減や，その他の標準的な演算を行う場合は，特別な記述法が用意されているので，そちらを使った方が簡単でよい．

Wolfram言語でプログラムを書いていて，あらかじめ作っておいたリストに後から要素を加えたいときがある．関数PrependToやAppendToを使うとこれができるようになる．

AppendTo[v,elem]とv=Append[v,elem]は機能的に等しいが，記述するには前者の方が使いやすいことが多いだろう．ただし，Wolframシステムで使われるリストの保存の仕方のため，特定のリストに要素の列を追加する操作は，普通，ネストした構造体（例えば，各レベルのサブリスト長を2としたリスト）を構築する操作より処理能率が悪い．そのような構造体を作るときは，常に，Flattenを作用させることで，それを単一リストにすることができる．

多くの種類の計算では，特定の添数で指定された複数の式からなる「配列」を使わなければいけないことがある．Wolfram言語で配列を構築するひとつの方法として，リストを使った方法が考えられる．a={x,y,z,…}のようなリストを定義しておけば，各要素を a[[i]]の形式で参照したり，それらを a[[i]]=value の書式で変更したりすることができる．ただし，この方法だとリストを構築する際に，あらかじめリストの全要素を埋めておく必要がある．

任意のときに任意な要素だけを埋めることができる配列を構築できるとより便利である．これを行うには，a[i]形式の式に対して定義を作成する．

式a[i]は，「添数付き」または「添字付き」変数ととらえることができる．

a[i]の形の式があるとき，「添数」iは数でなくても構わない．Wolfram言語では，添数の表すものは実際何でもよい．つまり，シンボルとしてある添数を使うことで，例えば，簡単なデータベースを構築することもできる．

「ユーザ定義の関数」において，ユーザ定義の関数をどう作成するか説明した．関数fの定義は，f[x_]=x^2のように普通記述する．（「ユーザ定義の関数」での定義では，演算子=ではなく，演算子:=を使った．:=と=の演算子のどちらを使ったらよいかは，「即時的な定義と遅延的な定義」を参照すること．）

定義f[x_]=x^2は，Wolfram言語に対して，パターンf[x_]にマッチする式が現れるたびに，それをx^2に置換するよう指示する．パターンf[x_]は，f[anything]という形式を持つすべての式にマッチするので，この定義は任意の「引数」を持った関数fすべてに適用される．

f[x_]=x^2のような関数定義は，「添数付きオブジェクトの定義」で触れた添数付き変数に関するf[a]=bのような定義と比較することができる．f[a]=bは，特定の式f[a]が現れるたびに，それをbに置換するよう指示はするが，他の「添数」を持ったfが現れても（例えば，f[y]）全く関知しない．

「関数」を定義するには，f[x]形の式に対して値を指定する必要がある．x は何でもよい．これは，どんな式でも表すパターンオブジェクトx_を持つパターンf[x_]に対して定義を与えることで行うことができる．

f[2]やf[a]に関する定義を作成するということは，名前をfとした「配列」の要素に値を与える，ということに相当する．一方，f[x_]に関して定義を作ることは，任意の「添数」を持った「配列要素」の集合に対して値を与える，ということに相当する．実際，どのような関数でも，添数を任意の変数とした配列としてとらえることもできる．

数学では，fは1つの「写像（マップ）」としてとらえることができる．つまり，f[1]とf[2]に対する値の定義とは，定義域の離散点に対応した写像による像を指定することになる．f[x_]に対して値を定義することは，点の連続体におけるfの像を指定することになる．

変換規則は，その適用先が式であってもパターンであっても定義することができる．また，f[1]やf[a]のような特定の式に対する定義と，f[x_]等のパターンに対する定義を一緒に混ぜて使うこともできる．

Wolfram言語では，数学関数の多くは，特殊定義と一般定義を組み合せて使うことで構築することができる．例えば，階乗関数を考える．この関数は，すでにWolfram言語に組み込まれているが（n!と書く），Wolfram言語の定義を使うことでユーザ自身でも構築することができる．

階乗関数に関する標準的な数学定義は，f[n_]:=n f[n-1];f[1]=1とすることで，ほとんど直接的にWolfram言語に入力することができる．この定義は，n が1以外の値のとき，f[n]はn f[n-1]で置換され，さらに，n が1,のとき，f[1]は単に1で置換されるものとする．

定義の列をWolframシステムで作ると，それらの定義は他の定義より，より一般的な定義であることがある．Wolframシステムは，一般定義は特殊な定義よりも後回しにされる，という原則に従っている．このため，規則の特殊ケースは，より一般的なケースより先に試される．

この動作は，「関数の定義」の例で示した階乗関数で決定的な役割を果たす．つまり，規則の入力された順序に関係なしに，Wolframシステムは，f[1]の特殊ケースの規則をf[n_]用の一般則の前に置く．このため，Wolframシステムがf[n]形のある式の値を探すときは，f[1]の特殊ケースを最初に試し，それが適用しない場合に限って，一般ケースであるf[n_]を試す．その結果，f[5]の値が要求されると，Wolframシステムは，f[1]に対応した「最終条件」が適用できるようになるまで，一般則を繰り返し使う．

もしも特殊則を一般則の前に使うという原則が守られなかったら，特殊則はより一般的な規則で常に「隠され」てしまう．上記の階乗の例で，もしf[n_]用の規則がf[1]の規則より優先されたなら，Wolframシステムがf[1]を評価しようとするときも，f[n_]の一般則が適用されてしまい，f[1]の特殊則がいつまでたっても使われないという状況に陥ってしまう．

上記の階乗関数の例では，どちらの規則がより一般的なものかがはっきりしている．しかし，与えられる規則にはっきりした適用順序を見出すことができないことがよくある．そのようなときは，Wolframシステムは，単純に入力された順序通りに規則を適用していく．

Wolframシステムは，多くの実践的なケースでは，いつある規則が他の規則より，より一般的であるかを認識することができるが，どんな場合でもそうかというとそうではない．例えば，2つの規則がともに/;による複雑な条件を含むとき，どちらがより一般的かは判断することが極めて困難である．決まった順序はないかもしれない．順序を判断できないとき，Wolframシステムは与えられた通りの順序で規則を保管する．

Wolfram言語で割当てを行うには，2つの違った方法があることに読者はすでに気が付いているかもしれない．つまり，lhs=rhs と lhs:=rhs である．これらの形の間にある基本的な違いは，いつ式 rhs が評価されるかにある．lhs=rhs は即時型の割当てを表し，右辺 rhs は定義した時点で評価される．これに対して，lhs:=rhs は遅延型の割当てを表し，rhs は，割当てが行われるときには評価されず，lhs の値が要求されるときに毎回評価される．

上の例から分かるように，=と:=はともに関数を定義する上で便利だが，違った意味を持っている．このため，状況に応じて使い分ける必要がある．

使い分けの目安として次の手順を取るとよい．割当てを，ある式の最終的な「値」を与えるものととらえるならば，演算子=を使う．また，割当てを，値を見出すための「コマンド」としてとらえるならば，演算子:=を使う．どちらかはっきりしないときは，通常，=ではなく，:=を使うと無難である．

関数の定義でおそらく，:=は，=より多く使われるだろうが，次に示す重要な場合には，必ず=を使い関数を定義しなければならない．ある計算を行い，シンボル的パラメータ 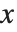により答が得られるとき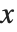， を各種の特定値としたときに結果がどうなるかを調べる必要がよく出てくる．そのようなときは，ひとつの方法として，演算子/.を使い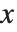， について適切な規則を適用することが考えられる．しかし，通常は，=を使い，引数を 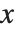とした関数を定義した方がより便利になる．

上の例において重要な点は，パターンx_に現れる名前xは特別な意味を持たないということである．他の任意の式に現れるxと同様に，単なるシンボルでしかない．

=と:=は，関数定義だけでなく変数への値の割当てにも使うことができる．x=value と入力すれば，値 value は即座に評価され，結果は x に割り当てられる．一方，x:=value と入力すると，value はすぐには評価されない．入力されたままの形で維持され，実際に 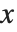が使われるときに毎回再評価される．

数珠つなぎに割当て関係を構築していく際は，即時型の割当てと遅延型の割当ての間にある違いは，特に重要である．

t:=rhs の遅延型の割当てを使えば，変化する「状況」に応じた値持つ変数を右辺に割り当てることができる．t を参照するときは，その都度，それが依存するオブジェクトの最新値が使われて右辺 rhs が再評価される．

上の例で，シンボルaはtの値を左右する「大域変数」として働く．パラメータをたくさん使う必要があり，また，それらの値をあまり変える必要がなければ，この割当て方法は便利でよいだろう．しかし，変数が他の変数への隠された依存性を持つようなときは，この方法で変数の割当てを行うとかえって混乱させるかもしれないので注意が必要である．関数を定義する際に，必要なすべてのパラメータを引数とすることで，依存性を明示化しておいた方がよい．

割当てに，即座に行うものと，後で行うものの2種類があるように，変換規則にも即時型と遅延型がある．

割当ての場合と同じように，置換する値が確定しているときは，->を使うようにし，また，式の値を求めるためのコマンドを与えるときには，:>を使うようにする．

:=を使い関数の定義を作成するとき，関数の値は，その要求があるたびに再計算される．計算の種類によっては，同じ関数の値を何度も要求するような状況が出てくる．そのようなときは，Wolfram言語が，求まったすべての関数値を覚えておくようにしておく．これを行うには，次の形式を使い関数を定義する．

これまでの説明で，f[x_]:=f[x]=f[x-1]+f[x-2]のような定義がどう働くか理解できたことと思う．f[x_]は，「プログラム」f[x]=f[x-1]+f[x-2]として定義される．関数fの値が要求されるときは，この「プログラム」が実行される．このプログラムは，最初に，f[x-1]+f[x-2]の値を計算し，次に，結果をf[x]として保存する．

数学の帰納的関係をプログラムするときは，一度計算した値を保持しておく形で関数を記述するとよい．通常は，帰納的関係は，整数の引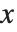数 を取る関数 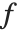の値を求める．この引数は 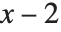，等を引数とした同じ関数の値から構成される．上で使った定義 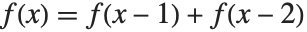はフィボナッチ(Fibonacci)の関数と呼ばれ，典型的な帰納的関係である．ここで重要な点は，もしも帰納的関係を繰り返し適用することで，例えば，を計算させる場合，の値を何回も計算するはめに陥る．そのような場合には，の値を覚えておき，将来必要になるときには，再計算をしないで参照するだけにする．

もちろん覚えさせて得する反面，どこかで損もする．計算は早くなるが，記憶のために余計なメモリが必要になる．したがって，むやみやたらには，値を保持するように指示をしない方がよい．この方法は，割合少ない個数の値しか生成しない関数に限って使う方がよいだろう．

Wolfram言語では f[args]=rhs や f[args]:=rhs の形で割当て式を定義すると，式がオブジェクト f に関連付けられる．例えば，?f と入力すると，表示にはこの定義が現れる．一般に，シンボル f を頭部とする式の定義は，f の下向きの値と呼ばれる．

Wolfram言語では，その逆の考えに基づいた上向きの値も使えるようになっている．上向きの値は，直接的な頭部ではないシンボルに定義を関連させるために使われる．

例として，Exp[g[x_]]:=rhs を考える．1つの可能性として，この定義はシンボルExpに関連付けることができるため，それをExpの下向きの値としてとらえることができる．しかし，このとらえ方は，式の構成や計算の効率を考えると最良の見方であるとはいえないだろう．

むしろExp[g[x_]]:=rhs がgに関連付けられていると考え，gの上向きの値としてとらえた方がよい．

単純なケースでは，f[g[x]]に対する定義を，f の下向きの値，または，g の上向きの値として与えても，計算される結果は変わらない．それでも，2つのとらえ方の内で，どちらか片方が他方に比べてより自然で，また，効率的になることがよくある．

どちらを取るかを判断する目安として，f[g[x]]の定義は，関数 f が g よりも使用頻度が高ければ g の上向きの値としてとらえる．これに従うと，Exp[g[x]]では，ExpはWolfram言語の組込み関数であり，g はユーザ定義の関数であろう．そのような場合は，Exp[g[x]]に対する定義は，g により満たされる関係を与えるものと通常とらえるだろう．つまり，定義をExpの下向きの値ととらえるよりは，g の上向きの値としてとらえた方がより自然である．

g[x_]+g[y_]は，完全形でPlus[g[x_],g[y_]]であるから，このパターンに対する定義は，Plusに対する下向きの値として与えることができる．それでも，ほとんどどんな場合でも，定義はgの上向きの値として与えた方がよい．

ある特定の関数が参照されるとき，Wolfram言語は，その関数に関連付けられた全定義を試す．g[x_]+g[y_]用の定義をPlusに関する下向きの値として作ると，Plusが現れるたびに，Wolfram言語はこの定義を使ってしまう．これは，式の加法が行われるたびにこの定義が判定されるため，非常に一般的な演算操作を遅くしてしまうことになる．

しかし，g[x_]+g[y_]用の定義をgの上向きの値として与えておけば，定義をgに関連付けることになる．この場合，Wolfram言語は，Plusのような関数でgが現れるときにだけこの定義を試す．gがPlusに比べてあまり使用されないとすると，この手順の方がより効率的になる．

上向きの値は，特定のオブジェクトの特性に関する「データベース」を構築するのによく使われる．上向きの値を使えば，作成する定義を，指定される特性にではなくこの定義にかかわるオブジェクトに関連付けることができる．

十分高いレベルに位置するシンボルであれば，それが何であっても，式に関する定義をそれに関連させることができる．f[args]形の式があるとき，あるシンボル g 自体または g を頭部とするオブジェクトが args に現れるのであれば，g に関する上向きの値は定義することができる．しかし，もし g が式の低レベルに現れるならば，それに定義を関連付けることはできない．

「式の意味」で説明したように，シンボルを「タグ」として使うことで式の「型」を指定することができる．例えば，複素数はWolfram言語でComplex[x,y]と表されるが，シンボルComplexは，該当オブジェクトが複素数であることを指定するためのタグとして働いている．

上向きの値を使うと，タグにより型を特定化されたオブジェクトに対して働く操作を指定することが簡便になる．例えば，型をquatとした抽象的な数学オブジェクトからなる1つのオブジェクトクラスを導入したいとする．このとき，この型のオブジェクトは，quat[data]という形式のWolfram言語式で表すことができる．

quatオブジェクトに，足し算や掛け算等の四則演算に関連した特別な性質を持たせたいときがある．このような性質は，quatに関する上向きの値をPlusやTimesに対して定義することで設定することができる．

quatの上向きの値をPlusのような演算に対して定義するとき，それは実効的にquatオブジェクトを包含させるべくPlusの定義域を拡張することに相当する．これは，加算される数がquat型のオブジェクトである場合には，加法に特殊則を使うようにWolfram言語に指示することになる．

quatオブジェクトを対象にした加法を定義する際，適当な下向きの値を割り当てた特殊な加法操作（例えば，quatPlus）を使うことも考えられる．しかし，普通は，標準の組込み関数Plusを使い加法を表せるが，quat型のオブジェクトがあるときに限り特殊な動作を指定することで加法操作に「過負荷」を掛けた方がより簡便になる．

上向きの値は，いわゆるオブジェクト指向のプログラミング手法を，部分的だが実現するのに使える．quat等のシンボルは特定の型のオブジェクトを表すので，quatに関した各種の上向きの値は「メソッド」を指定するために使える．メソッドとは，特定の操作が施されるときや，特定の「メッセージ」が受け取られるときに，quatオブジェクトがどう動作すべきかを定義するものを指す．

f[x_]:=value のような定義を作ると，Wolfram言語は，任意の関数fが現れるたびに与えられた値を使う．しかし，場合によっては，値を，数値が要求されるときに限って使われるものとして定義したいことがある．

数値は，関数に対してでもシンボルに対してでも定義することができる．定義された数値は，NIntegrateやFindRoot等のすべての組込み関数により使われる．

数値は基本的に上向きの値と同様に扱われる．f に対して数値的な値を定義するとき，この定義は，f の上向きの値を数値解析関数Nで使うためのものとして内部に保管される．

変換規則は，どのような式にでも定義することができる．ユーザ定義の関数だけに限らず，Wolfram言語に組込み済みの内部関数についても同様である．このため，変換規則を使い，組込み関数の機能を拡張したり，目的に合うように変更したりすることができる．

この機能は強力であるとともに危険性もはらんでいる．Wolfram言語は，与えられた規則をそのまま適用する．間違った規則が与えられると，Wolfram言語の答も間違ったものになってしまう．

誤入力による組込み関数の変更がないように，すべての組込み関数には「プロテクト（保護）」がかけられており，再定義ができないようになっている．このため，組込み関数に関して定義を与えるには，まず，この保護機能を解除する必要がある．そして，定義を与えた後には，将来の誤入力を防ぐために再度保護機能を有効にしておく．

ユーザ指定の定義は，Wolfram言語の組込み機能を上書きしてしまう．また，ユーザの定義は，通常，組込み定義より先に使われる．

Wolfram言語に組込み済みの規則は，なるべく多くの計算問題に対応できるように作られている．それでも，問題が非常に特殊なものだと，組込み定義ではユーザの使いたい特別な計算手法に対応できない場合も出てくる．そのようなときは，ユーザ自身で特別な規則を構築し，組込み規則を上書きしておく．

定義された式は，すべて変換規則のリストとして保管される．特定のシンボルが参照されるとき，それに関連付けられた規則のリストが選択され，それらの規則がすべて試される．

ほとんどの場合，ユーザ定義に関係付けられた変換規則そのものに直接アクセスする必要はないだろう．その代り，単に lhs=rhs と lhs=.を使い，規則を追加したり削除したりすることができる．しかし，場合によっては，実際の規則に直接アクセスできると便利になる．

DownValuesとUpValuesにより返される規則は，右辺と左辺がともに未評価の状態にある．左辺は評価保留の関数HoldPatternで覆われ，規則は遅延され，右辺は即時的には評価されない．

「関数の定義」で説明したように，特殊な定義は，より一般的な定義よりも先に適用される．しかし，一般に任意な定義式の間で優先順位をはっきりさせるのは困難である．さらに，Wolfram言語内部で採用される順位ではなく，ユーザ自身で決定した順位を使いたい場合も出てくるだろう．これを行うには，DownValuesとUpValuesからリストで得られる規則を再構成すればよい．