Transformation Rules and Definitions
Transformation Rules and Definitions
| expr/.lhs->rhs | apply a transformation rule to expr |
| expr/.{lhs1->rhs1,lhs2->rhs2,…} | try a sequence of rules on each part of expr |
Functions such as Solve and NSolve return lists whose elements are lists of rules, each representing a solution:
When you use expr/.rules, each rule is tried in turn on each part of expr. As soon as a rule applies, the appropriate transformation is made, and the resulting part is returned.
A result is returned as soon as the rule has been applied, so the inner instance of h is not replaced:
Sometimes you may need to go on applying rules over and over again, until the expression you are working on no longer changes. You can do this using the repeated replacement operation expr//.rules (or ReplaceRepeated[expr,rules]).
| expr/.rules | try rules once on each part of expr |
| expr//.rules | try rules repeatedly until the result no longer changes |
With the single replacement operator /. each rule is tried only once on each part of the expression:
With the repeated replacement operator //. the rules are tried repeatedly until the expression no longer changes:
With the repeated replacement operator, the rule is applied repeatedly, until the result no longer changes:
When you use //. (pronounced "slash‐slash‐dot"), the Wolfram Language repeatedly passes through your expression, trying each of the rules given. It goes on doing this until it gets the same result on two successive passes.
If you give a set of rules that is circular, then //. can keep on getting different results forever. In practice, the maximum number of passes that //. makes on a particular expression is determined by the setting for the option MaxIterations. If you want to keep going for as long as possible, you can use ReplaceRepeated[expr,rules,MaxIterations->Infinity]. You can always stop by explicitly interrupting the Wolfram Language.
By setting the option MaxIterations, you can explicitly tell ReplaceRepeated how many times to try the rules you give:
The replacement operators /. and //. share the feature that they try each rule on every subpart of your expression. On the other hand, Replace[expr,rules] tries the rules only on the whole of expr, and not on any of its subparts.
You can use Replace, together with functions like Map and MapAt, to control exactly which parts of an expression a replacement is applied to. Remember that you can use the function ReplacePart[expr,new,pos] to replace part of an expression with a specific object.
Without a level specification, Replace applies rules only to the whole expression:
| expr/.rules | apply rules to all subparts of expr |
| Replace[expr,rules] | apply rules to the whole of expr only |
| Replace[expr,rules,levspec] | apply rules to parts of expr on levels specified by levspec |
Replace returns the result from using the first rule that applies:
ReplaceList gives a list of the results from every rule that applies:
If a single rule can be applied in several ways, ReplaceList gives a list of all the results:
| Replace[expr,rules] | apply rules in one way only |
| ReplaceList[expr,rules] | apply rules in all possible ways |
You can manipulate lists of transformation rules in the Wolfram Language just like other symbolic expressions. It is common to assign a name to a rule or set of rules.
You can use lists of rules to represent mathematical and other relations. Typically you will find it convenient to give names to the lists, so that you can easily specify the list you want in a particular case.
In most situations, it is only one rule from any given list that actually applies to a particular expression. Nevertheless, the /. operator tests each of the rules in the list in turn. If the list is very long, this process can take a long time.
The Wolfram Language allows you to preprocess lists of rules so that /. can operate more quickly on them. You can take any list of rules and apply the function Dispatch to them. The result is a representation of the original list of rules, but including dispatch tables which allow /. to "dispatch" to potentially applicable rules immediately, rather than testing all the rules in turn.
| Dispatch[rules] | create a representation of a list of rules that includes dispatch tables |
| expr/.drules | apply rules that include dispatch tables |
For long lists of rules, you will find that setting up dispatch tables makes replacement operations much faster. This is particularly true when your rules are for individual symbols or other expressions that do not involve pattern objects. Once you have built dispatch tables in such cases, you will find that the /. operator takes a time that is more or less independent of the number of rules you have. Without dispatch tables, however, /. will take a time directly proportional to the total number of rules.
The replacement operator /. allows you to apply transformation rules to a specific expression. Often, however, you want to have transformation rules automatically applied whenever possible.
You can do this by assigning explicit values to Wolfram Language expressions and patterns. Each assignment specifies a transformation rule to be applied whenever an expression of the appropriate form occurs.
| expr/.lhs->rhs | apply a transformation rule to a specific expression |
| lhs=rhs | assign a value which defines a transformation rule to be used whenever possible |
By assigning a value to x, you tell the Wolfram Language to apply a transformation rule for x whenever possible:
You should realize that except inside constructs like Module and Block, all assignments you make in a Wolfram Language session are permanent. They continue to be used for the duration of the session, unless you explicitly clear or overwrite them.
The fact that assignments are permanent means that they must be made with care. Probably the single most common mistake in using the Wolfram Language is to make an assignment for a variable like x at one point in your session, and then later to use x having forgotten about the assignment you made.
There are several ways to avoid this kind of mistake. First, you should avoid using assignments whenever possible, and instead use more controlled constructs such as the /. replacement operator. Second, you should explicitly use the deassignment operator =. or the function Clear to remove values you have assigned when you have finished with them.
Another important way to avoid mistakes is to think particularly carefully before assigning values to variables with common or simple names. You will often want to use a variable such as x as a symbolic parameter. But if you make an assignment such as x=3, then x will be replaced by 3 whenever it occurs, and you can no longer use x as a symbolic parameter.
In general, you should be sure not to assign permanent values to any variables that you might want to use for more than one purpose. If at one point in your session you wanted the variable c to stand for the speed of light, you might assign it a value such as 3.*10^8. But then you cannot use c later in your session to stand, say, for an undetermined coefficient. One way to avoid this kind of problem is to make assignments only for variables with more explicit names, such as SpeedOfLight.
| x=. | remove the value assigned to the object x |
| Clear[x,y,…] | clear all the values of x, y, … |
Particularly when you write procedural programs in the Wolfram Language, you will often need to modify the value of a particular variable repeatedly. You can always do this by constructing the new value and explicitly performing an assignment such as x=value. The Wolfram Language, however, provides special notations for incrementing the values of variables, and for some other common cases.
| i++ | increment the value of i by 1 |
| i-- | decrement i |
| ++i | pre‐increment i |
| --i | pre‐decrement i |
| i+=di | add di to the value of i |
| i-=di | subtract di from i |
| x*=c | multiply x by c |
| x/=c | divide x by c |
| x=y=value | assign the same value to both x and y |
| {x,y}={value1,value2} | assign different values to x and y |
| {x,y}={y,x} | interchange the values of x and y |
When you write programs in the Wolfram Language, you will sometimes find it convenient to take a list, and successively add elements to it. You can do this using the functions PrependTo and AppendTo.
| PrependTo[v,elem] | prepend elem to the value of v |
| AppendTo[v,elem] | append elem |
| v={v,elem} | make a nested list containing elem |
Although AppendTo[v,elem] is always equivalent to v=Append[v,elem], it is often a convenient notation. However, you should realize that because of the way the Wolfram System stores lists, it is usually less efficient to add a sequence of elements to a particular list than to create a nested structure that consists, for example, of lists of length 2 at each level. When you have built up such a structure, you can always reduce it to a single list using Flatten.
You can use Flatten to unravel the structure:
In many kinds of calculations, you need to set up "arrays" that contain sequences of expressions, each specified by a certain index. One way to implement arrays in the Wolfram Language is by using lists. You can define a list, say a={x,y,z,…}, then access its elements using a[[i]], or modify them using a[[i]]=value. This approach has a drawback, however, in that it requires you to fill in all the elements when you first create the list.
Often, it is more convenient to set up arrays in which you can fill in only those elements that you need at a particular time. You can do this by making definitions for expressions such as a[i].
| a[i]=value | add or overwrite a value |
| a[i] | access a value |
| a[i]=. | remove a value |
| ?a | show all defined values |
| Clear[a] | clear all defined values |
| Table[a[i],{i,1,n}] or Array[a,n] | convert to an explicit List |
When you have an expression of the form a[i], there is no requirement that the "index" i be a number. In fact, the Wolfram Language allows the index to be any expression whatsoever. By using indices that are symbols, you can for example build up simple databases in the Wolfram Language.
You can use these definitions wherever you want. You have not yet assigned a value for area[pentagon]:
"Defining Functions" discusses how you can define functions in the Wolfram Language. In a typical case, you would type in f[x_]=x^2 to define a function f. (Actually, the definitions in "Defining Functions" use the := operator, rather than the = one. "Immediate and Delayed Definitions" explains exactly when to use each of the := and = operators.)
The definition f[x_]=x^2 specifies that whenever the Wolfram Language encounters an expression that matches the pattern f[x_], it should replace the expression by x^2. Since the pattern f[x_] matches all expressions of the form f[anything], the definition applies to functions f with any "argument".
Function definitions like f[x_]=x^2 can be compared with definitions like f[a]=b for indexed variables discussed in "Making Definitions for Indexed Objects". The definition f[a]=b specifies that whenever the particular expression f[a] occurs, it is to be replaced by b. But the definition says nothing about expressions such as f[y], where f appears with another "index".
To define a "function", you need to specify values for expressions of the form f[x], where the argument x can be anything. You can do this by giving a definition for the pattern f[x_], where the pattern object x_ stands for any expression.
| f[x]=value | definition for a specific expression x |
| f[x_]=value | definition for any expression, referred to as x |
Making definitions for f[2] or f[a] can be thought of as being like giving values to various elements of an "array" named f. Making a definition for f[x_] is like giving a value for a set of "array elements" with arbitrary "indices". In fact, you can actually think of any function as being like an array with an arbitrarily variable index.
In mathematical terms, you can think of f as a mapping. When you define values for, say, f[1] and f[2], you specify the image of this mapping for various discrete points in its domain. Defining a value for f[x_] specifies the image of f on a continuum of points.
When the specific expression f[x] appears, it is replaced by u. Other expressions of the form f[argument] are, however, not modified:
The old definition for the specific expression f[x] is still used, but the new general definition for f[x_] is now used to find a value for f[y]:
The Wolfram Language allows you to define transformation rules for any expression or pattern. You can mix definitions for specific expressions such as f[1] or f[a] with definitions for patterns such as f[x_].
Many kinds of mathematical functions can be set up by mixing specific and general definitions in the Wolfram Language. As an example, consider the factorial function. This particular function is in fact built into the Wolfram Language (it is written n!). But you can use Wolfram Language definitions to set up the function for yourself.
The standard mathematical definition for the factorial function can be entered almost directly into the Wolfram Language, in the form f[n_]:=n f[n-1];f[1]=1. This definition specifies that for any n, f[n] should be replaced by n f[n-1], except that when n is 1, f[1] should simply be replaced by 1.
When you make a sequence of definitions in the Wolfram System, some may be more general than others. The Wolfram System follows the principle of trying to put more general definitions after more specific ones. This means that special cases of rules are typically tried before more general cases.
This behavior is crucial to the factorial function example given in "Making Definitions for Functions". Regardless of the order in which you entered them, the Wolfram System will always put the rule for the special case f[1] ahead of the rule for the general case f[n_]. This means that when the Wolfram System looks for the value of an expression of the form f[n], it tries the special case f[1] first, and only if this does not apply, it tries the general case f[n_]. As a result, when you ask for f[5], the Wolfram System will keep on using the general rule until the "end condition" rule for f[1] applies.
If the Wolfram System did not follow the principle of putting special rules before more general ones, then the special rules would always be "shadowed" by more general ones. In the factorial example, if the rule for f[n_] was ahead of the rule for f[1], then even when the Wolfram System tried to evaluate f[1], it would use the general f[n_] rule, and it would never find the special f[1] rule.
In the factorial function example used above, it is clear which rule is more general. Often, however, there is no definite ordering in generality of the rules you give. In such cases, the Wolfram System simply tries the rules in the order you give them.
Although in many practical cases, the Wolfram System can recognize when one rule is more general than another, you should realize that this is not always possible. For example, if two rules both contain complicated /; conditions, it may not be possible to work out which is more general, and, in fact, there may not be a definite ordering. Whenever the appropriate ordering is not clear, the Wolfram System stores rules in the order you give them.
You may have noticed that there are two different ways to make assignments in the Wolfram Language: lhs=rhs and lhs:=rhs. The basic difference between these forms is when the expression rhs is evaluated. lhs=rhs is an immediate assignment, in which rhs is evaluated at the time when the assignment is made. lhs:=rhs, on the other hand, is a delayed assignment, in which rhs is not evaluated when the assignment is made, but is instead evaluated each time the value of lhs is requested.
| lhs=rhs
(immediate assignment)
| rhs is evaluated when the assignment is made |
| lhs:=rhs
(delayed assignment)
| rhs is evaluated each time the value of lhs is requested |
The definition now stored is the result of the Expand command:
As you can see from the example above, both = and := can be useful in defining functions, but they have different meanings, and you must be careful about which one to use in a particular case.
One rule of thumb is the following. If you think of an assignment as giving the final "value" of an expression, use the = operator. If instead you think of the assignment as specifying a "command" for finding the value, use the := operator. If in doubt, it is usually better to use the := operator than the = one.
| lhs=rhs | rhs is intended to be the "final value" of lhs (e.g. f[x_]=1-x^2) |
| lhs:=rhs | rhs gives a "command" or "program" to be executed whenever you ask for the value of lhs (e.g. f[x_]:=Expand[1-x^2]) |
Although := is probably used more often than = in defining functions, there is one important case in which you must use = to define a function. If you do a calculation, and get an answer in terms of a symbolic parameter 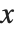 , you often want to go on and find results for various specific values of
, you often want to go on and find results for various specific values of 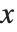 . One way to do this is to use the /. operator to apply appropriate rules for
. One way to do this is to use the /. operator to apply appropriate rules for 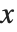 in each case. It is usually more convenient, however, to use = to define a function whose argument is
in each case. It is usually more convenient, however, to use = to define a function whose argument is 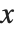 .
.
An important point to notice in the example above is that there is nothing special about the name x that appears in the x_ pattern. It is just a symbol, indistinguishable from an x that appears in any other expression.
You can use = and := not only to define functions, but also to assign values to variables. If you type x=value, then value is immediately evaluated, and the result is assigned to x. On the other hand, if you type x:=value, then value is not immediately evaluated. Instead, it is maintained in an unevaluated form, and is evaluated afresh each time 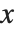 is used.
is used.
Here RandomReal[] is maintained in an unevaluated form, to be evaluated afresh each time r2 is used:
The value of r1 never changes. Every time r2 is used, however, a new pseudorandom number is generated:
The distinction between immediate and delayed assignments is particularly important when you set up chains of assignments.
Here a+2 is maintained in an unevaluated form, to be evaluated every time the value of rd is requested:
You can use delayed assignments such as t:=rhs to set up variables whose values you can find in a variety of different "environments". Every time you ask for t, the expression rhs is evaluated using the current values of the objects on which it depends.
In the example above, the symbol a acts as a "global variable", whose value affects the value of t. When you have a large number of parameters, many of which change only occasionally, you may find this kind of setup convenient. However, you should realize that implicit or hidden dependence of one variable on others can often become quite confusing. When possible, you should make all dependencies explicit, by defining functions which take all necessary parameters as arguments.
Just as you can make immediate and delayed assignments in the Wolfram Language, so you can also set up immediate and delayed transformation rules.
Here the right‐hand side of the rule is maintained in an unevaluated form, to be evaluated every time the rule is used:
In analogy with assignments, you should typically use -> when you want to replace an expression with a definite value, and you should use :> when you want to give a command for finding the value.
When you make a function definition using :=, the value of the function is recomputed every time you ask for it. In some kinds of calculations, you may end up asking for the same function value many times. You can save time in these cases by having the Wolfram Language remember all the function values it finds. Here is an "idiom" for defining a function that does this.
If you ask for f[5] again, the Wolfram Language can just look up the value immediately; it does not have to recompute it:
You can see how a definition like f[x_]:=f[x]=f[x-1]+f[x-2] works. The function f[x_] is defined to be the "program" f[x]=f[x-1]+f[x-2]. When you ask for a value of the function f, the "program" is executed. The program first calculates the value of f[x-1]+f[x-2], then saves the result as f[x].
It is often a good idea to use functions that remember values when you implement mathematical recursion relations in the Wolfram Language. In a typical case, a recursion relation gives the value of a function 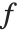 with an integer argument
with an integer argument 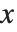 in terms of values of the same function with arguments
in terms of values of the same function with arguments  ,
, 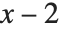 , etc. The Fibonacci function definition
, etc. The Fibonacci function definition 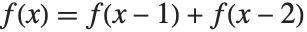 used above is an example of this kind of recursion relation. The point is that if you calculate say
used above is an example of this kind of recursion relation. The point is that if you calculate say  by just applying the recursion relation over and over again, you end up having to recalculate quantities like
by just applying the recursion relation over and over again, you end up having to recalculate quantities like  many times. In a case like this, it is therefore better just to remember the value of
many times. In a case like this, it is therefore better just to remember the value of  , and look it up when you need it, rather than having to recalculate it.
, and look it up when you need it, rather than having to recalculate it.
There is of course a trade‐off involved in remembering values. It is faster to find a particular value, but it takes more memory space to store all of them. You should usually define functions to remember values only if the total number of different values that will be produced is comparatively small, or the expense of recomputing them is very great.
When you make a definition in the form f[args]=rhs or f[args]:=rhs, the Wolfram Language associates your definition with the object f. This means, for example, that such definitions are displayed when you type ?f. In general, definitions for expressions in which the symbol f appears as the head are termed downvalues of f.
The Wolfram Language however also supports upvalues, which allow definitions to be associated with symbols that do not appear directly as their head.
Consider for example a definition like Exp[g[x_]]:=rhs. One possibility is that this definition could be associated with the symbol Exp, and considered as a downvalue of Exp. This is however probably not the best thing either from the point of view of organization or efficiency.
Better is to consider Exp[g[x_]]:=rhs to be associated with g, and to correspond to an upvalue of g.
It is not associated with Exp:
In simple cases, you will get the same answers to calculations whether you give a definition for f[g[x]] as a downvalue for f or an upvalue for g. However, one of the two choices is usually much more natural and efficient than the other.
A good rule of thumb is that a definition for f[g[x]] should be given as an upvalue for g in cases where the function f is more common than g. Thus, for example, in the case of Exp[g[x]], Exp is a built‐in Wolfram Language function, while g is presumably a function you have added. In such a case, you will typically think of definitions for Exp[g[x]] as giving relations satisfied by g. As a result, it is more natural to treat the definitions as upvalues for g than as downvalues for Exp.
Since the full form of the pattern g[x_]+g[y_] is Plus[g[x_],g[y_]], a definition for this pattern could be given as a downvalue for Plus. It is almost always better, however, to give the definition as an upvalue for g.
In general, whenever the Wolfram Language encounters a particular function, it tries all the definitions you have given for that function. If you had made the definition for g[x_]+g[y_] a downvalue for Plus, then the Wolfram Language would have tried this definition whenever Plus occurs. The definition would thus be tested every time the Wolfram Language added expressions together, making this very common operation slower in all cases.
However, by giving a definition for g[x_]+g[y_] as an upvalue for g, you associate the definition with g. In this case, the Wolfram Language only tries the definition when it finds a g inside a function such as Plus. Since g presumably occurs much less frequently than Plus, this is a much more efficient procedure.
| f[g]^=value or f[g[args]]^=value | |
make assignments to be associated with g, rather than f | |
| f[g]^:=value or f[g[args]]^:=value | |
make delayed assignments associated with g | |
| f[arg1,arg2,…]^=value | make assignments associated with the heads of all the argi |
A typical use of upvalues is in setting up a "database" of properties of a particular object. With upvalues, you can associate each definition you make with the object that it concerns, rather than with the property you are specifying.
In general, you can associate definitions for an expression with any symbol that occurs at a sufficiently high level in the expression. With an expression of the form f[args], you can define an upvalue for a symbol g so long as either g itself, or an object with head g, occurs in args. If g occurs at a lower level in an expression, however, you cannot associate definitions with it.
| f[…]:=rhs | downvalue for f |
| f/:f[g[…]][…]:=rhs | downvalue for f |
| g/:f[…,g,…]:=rhs | upvalue for g |
| g/:f[…,g[…],…]:=rhs | upvalue for g |
As discussed in "The Meaning of Expressions", you can use Wolfram Language symbols as "tags", to indicate the "type" of an expression. For example, complex numbers in the Wolfram Language are represented internally in the form Complex[x,y], where the symbol Complex serves as a tag to indicate that the object is a complex number.
Upvalues provide a convenient mechanism for specifying how operations act on objects that are tagged to have a certain type. For example, you might want to introduce a class of abstract mathematical objects of type quat. You can represent each object of this type by a Wolfram Language expression of the form quat[data].
In a typical case, you might want quat objects to have special properties with respect to arithmetic operations such as addition and multiplication. You can set up such properties by defining upvalues for quat with respect to Plus and Times.
When you define an upvalue for quat with respect to an operation like Plus, what you are effectively doing is to extend the domain of the Plus operation to include quat objects. You are telling the Wolfram Language to use special rules for addition in the case where the things to be added together are quat objects.
In defining addition for quat objects, you could always have a special addition operation, say quatPlus, to which you assign an appropriate downvalue. It is usually much more convenient, however, to use the standard Wolfram Language Plus operation to represent addition, but then to "overload" this operation by specifying special behavior when quat objects are encountered.
You can think of upvalues as a way to implement certain aspects of object‐oriented programming. A symbol like quat represents a particular type of object. Then the various upvalues for quat specify "methods" that define how quat objects should behave under certain operations, or on receipt of certain "messages".
If you make a definition such as f[x_]:=value, the Wolfram Language will use the value you give for any f function it encounters. In some cases, however, you may want to define a value that is to be used specifically when you ask for numerical values.
| expr=value | define a value to be used whenever possible |
| N[expr]=value | define a value to be used for numerical approximation |
Defining the numerical value does not tell the Wolfram Language anything about the ordinary value of f:
If you ask for a numerical approximation, however, the Wolfram Language uses the numerical values you have defined:
You can define numerical values for both functions and symbols. The numerical values are used by all numerical Wolfram Language functions, including NIntegrate, FindRoot, and so on.
| N[expr]=value | define a numerical value to be used when default numerical precision is requested |
| N[expr,{n,Infinity}]=value | define a numerical value to be used when n‐digit precision and any accuracy is requested |
This defines a numerical value for the symbol const, using 4n+5 terms in the product for n‐digit precision:
The Wolfram Language treats numerical values essentially like upvalues. When you define a numerical value for f, the Wolfram Language effectively enters your definition as an upvalue for f with respect to the numerical evaluation operation N.
The Wolfram Language allows you to define transformation rules for any expression. You can define such rules not only for functions that you add to the Wolfram Language, but also for intrinsic functions that are already built into the Wolfram Language. As a result, you can enhance, or modify, the features of built‐in Wolfram Language functions.
This capability is powerful, but potentially dangerous. The Wolfram Language will always follow the rules you give it. This means that if the rules you give are incorrect, then the Wolfram Language will give you incorrect answers.
To avoid the possibility of changing built‐in functions by mistake, the Wolfram Language "protects" all built‐in functions from redefinition. If you want to give a definition for a built‐in function, you have to remove the protection first. After you give the definition, you should usually restore the protection, to prevent future mistakes.
This removes protection for Log:
Now you can give your own definitions for Log. This particular definition is not mathematically correct, but the Wolfram Language will still allow you to give it:
The Wolfram Language will use your definitions whenever it can, whether they are mathematically correct or not:
This removes the incorrect definition for Log:
This restores the protection for Log:
Definitions you give can override built‐in features of the Wolfram Language. In general, the Wolfram Language tries to use your definitions before it uses built‐in definitions.
The rules that are built into the Wolfram Language are intended to be appropriate for the broadest range of calculations. In specific cases, however, you may not like what the built‐in rules do. In such cases, you can give your own rules to override the ones that are built in.
| DownValues[f] | give the list of downvalues of f |
| UpValues[f] | give the list of upvalues of f |
| DownValues[f]=rules | set the downvalues of f |
| UpValues[f]=rules | set the upvalues of f |
The Wolfram Language effectively stores all definitions you give as lists of transformation rules. When a particular symbol is encountered, the lists of rules associated with it are tried.
Under most circumstances, you do not need direct access to the actual transformation rules associated with definitions you have given. Instead, you can simply use lhs=rhs and lhs=. to add and remove rules. In some cases, however, you may find it useful to have direct access to the actual rules.
Notice that the rules returned by DownValues and UpValues are set up so that neither their left‐ nor right‐hand sides get evaluated. The left‐hand sides are wrapped in HoldPattern, and the rules are delayed, so that the right‐hand sides are not immediately evaluated.
As discussed in "Making Definitions for Functions", the Wolfram Language tries to order definitions so that more specific ones appear before more general ones. In general, however, there is no unique way to make this ordering, and you may want to choose a different ordering from the one that the Wolfram Language chooses by default. You can do this by reordering the list of rules obtained from DownValues or UpValues.