变换规则和定义

运用变换规则 立即定义和延时定义
一组变换规则的操作保留已有值的函数
定义将定义与不同的符号相关联
特殊形式的赋值定义数量值
定义带标号的对象修改内置函数
定义函数值集的操作
定义的顺序
运用变换规则
expr/.lhs->rhs
对 expr 运用变换规则
expr/.{lhs1->rhs1,lhs2->rhs2,…}
将一列变换规则用于 expr 的每一项
运用变换规则.
在表达式上，替换运算符 /. 的使用：
可给出一列变换规则，将每个规则分别用到表达式的每一项：
expr/.{rules1,rules2,…}
将规则 rulesi 中的每个用于表达式 expr
运用一列变换规则.
通过一列规则就可以得到一列结果：
Solve 和 NSolve 等函数的返回值是一列规则，每个规则代表一个解：
运用这些规则可以得到一列结果，每个结果都对应一个解：
expr/.rules 将每一个规则逐次用到 expr 的每一项. 在此过程中进行相应的变换以得到结果.
先用规则 x^3，当它无法运用时用规则 x^n_：
规则一旦使用就立即产生结果，故里面的 h 还没有变：
替换 expr/.rules 中的每个规则对 expr 中的每一项只使用一次.
由于每个规则正好用一次，所以这里是交换 x 和 y：
可以用这种形式一个接一个地运用一组规则：
有时需要反复使用规则，直到表达式不再变换为止，这可通过反复替换运算 expr//.rules （或 ReplaceRepeated[expr,rules]）来实现.
expr/.rules
在 expr 的每一项中用变换规则一次
expr//.rules
重复使用规则直到结果不再变化为止
一次或多次重复使用规则.
单一替代运算 /. 使规则在表达式中各项上仅用一次：
重复替代运算 //. 使得规则被反复使用直到表达式不再变化为止：
此处规则仅使用一次：
用重复替换运算反复使用规则直到结果不再变化为止：
用 //. 时，Wolfram 语言将给定的规则反复使用到表达式上，直到相继的两个结果相同为止.
当使用一系列循环规则时，//. 能一直得到不同的结果. 在实际操作中，对一个特定表达式 //. 所能进行的最大循环次数取决于选项的设置. 用可选项 MaxIterations 可以确定对一个表达式的迭代次数. 当需要一直替换下去时，可以用 ReplaceRepeated[expr,rules,MaxIterations->Infinity] 来实现. 通过中断 Wolfram 语言总可以停止迭代.
通过可选项 MaxIterations，可以明确指出 ReplaceRepeated 在运用给定规则时的重复次数：
替换运算 /. 和 //. 的特点是将每个规则用在表达式的各项上，而 Replace[expr,rules] 将规则用在整个表达式 expr 上，不能用于表达式的一部分.
可以把 Replace 和 Map 以及 MapAt 等共同来指定规则用在表达式的哪一部分上. 另外， ReplacePart[expr,new,pos] 可以用给定的目标来代替表达式的项.
操作符 /. 将规则运用到表达式的每一项：
没有指定层时，Replace 仅将规则用于整个表达式：
这里没有进行任何替换：
将规则运用到第2层从而替换了 x：
expr/.rules
将规则运用于表达式 expr 的子项
Replace[expr,rules]
仅将规则运用于整个表达式 expr
Replace[expr,rules,levspec]
将规则用到由 levspec 指定层表达式 expr 的项上
对整个表达式运用规则.
Replace 给出使用第一个规则后的结果：
ReplaceList 给出一列规则使用后的结果：
当一个规则有多种使用方式时，ReplaceList 给出所有的结果：
此处给出了将原集合分解为两个集合的方式：
找出由同样元素包在侧面的所有子集：
Replace[expr,rules]
仅以一种方式用 rules
ReplaceList[expr,rules]
以所有可能的方式使用 rules
用一种方式或所有可能方式运用规则.
一组变换规则的操作
在 Wolfram 语言中，对规则命名后，就可以像操作符号表达式一样对一组规则进行操作.
将三角函数的展开式规则命名为 sinexp：
现在可以用名来调用规则：
你可以用规则列表来表示数学关系和其他关系. 通常情况下，对规则列表进行命名，然后在使用时，通过其命名就可以很容易的调用这些规则.
大多数情况下，一组规则中仅有一个作用于一个表达式. 然而，/. 操作符依次测试表中的所有规则. 当表中规则很多时，这需要很长时间.
Wolfram 语言为了提高 /. 的运行速度，可以先对一组规则进行处理，其方法是让 Dispatch 作用在这组规则上. Dispatch 函数作用的结果还是这一组规则，但它产生了一个分派表. 该分派表使 /. 不再逐个测试每个规则，而立即转到可使用的规则上去.
此处给出了前5个阶乘的规则：
建立分派表使规则运用得更快：
通过 /. 操作符来运用这些规则：
Dispatch[rules]
产生一列具有分派表的规则
expr/.drules
产生有分派表的规则
产生和使用分派表.
对于较长的规则列表，用了分派表之后可以使一列规则的替换运行得很快，当这些规则不是模式，而是一些单个符号或表达式时更显示出优势，用了分派表时就会发现 /. 操作符所花的时间几乎与规则的数量无关，而没有分派表时，/. 所花的时间与规则的数量成比例.
定义
替换运算 /. 将规则作用于一个表达式. 但经常需要在可能的情况下自动使用变换规则.
这可以通过对 Wolfram 语言表达式和模式赋值来实现. 赋值表明适当形式的表达式出现时就使用规则.
expr/.lhs->rhs
将规则用于一个表达式
lhs=rhs
赋值使规则可能时立即使用
人工和自动应用变换规则.
对指定的表达式使用关于 x 的变换规则：
通过对 x 赋值，可以告诉 Wolfram 语言对后面的任何 x 使用变换规则：
现在 x 自动地进行变换：
除 Module 和 Block 等一些内部结构外，在 Wolfram 语言中的所有赋值都是永久 的. 若没有清除或改写它们，在 Wolfram 语言的同一个进程中所赋值保持不变.
赋值的永久性意味着使用时要特别慎重. 一个在使用 Wolfram 语言时，常犯的错误是在后面使用 x 时忘记或误用了前面 x 的赋值.
为了减少这一错误，可能时尽量避免赋值而用替换运算 /. 等，也可以在任务完成后立即用 =. 或函数 Clear 去清除所赋的值.
另外一种避免这一错误的途径是对常用或简单的变量名赋值时要仔细考虑. 例如，经常使用变量名 x 作为符号参数. 但是如果用 x=3 赋值后，以后出现的 x 都用 3 代替，且以后也再不能将 x 当作一个符号参数使用.
一般来说，不要对有几种用途的变量赋值. 例如，若在某处用 c 变量表示光速 3.*10^8. 则以后就不能将 c 用作一个待定参数. 避免这种情况的一种途径是对光速用更加明确的变量名，如 SpeedOfLight.
x=.
清除对 x 的赋值
Clear[x,y,…]
清除变量 x，y，… 的所有值
清除赋值.
当 x 在前面赋过值时，就不一定能给出所期望的结果：
清除 x 以前的值：
现在给出了正确的结果：
特殊形式的赋值
在 Wolfram 语言编程中，经常需要用 x=value 等语句不断改变一些变量的值. Wolfram 语言在一些常用情况提供了通过增量修改变量的方法.
i++
i 加 1
i--
i 减 1
++i
先给 i 加 1
--i
先给 i 减 1
i+=di
i 加 di
i-=di
i 减 di
x*=c
x 乘以 c
x/=c
x 除以 c
修改变量的值.
变量 t 赋值为 7x：
t 的值增加 18x：
观察 t 值的变化：
先将 t 的值设为 8，再乘以 7，给出最后 t 的结果：
i++ 的值是 i 增加以前的值：
++i 是 i 增加以后的值：
x=y=value
对 x 和 y 赋同一值
{x,y}={value1,value2}
对 x 和 y 赋不同的值
{x,y}={y,x}
交换 x 和 y 的值
同时对几个变量赋值.
给 x 赋值 5，y 赋值 8：
交换 x 和 y 的值：
现在 x 的值为 8：
y 的值为 5：
可以用赋值语句任意交换变量的值：
在 Wolfram 语言编程时，通过逐步增加元素的方法来构造一个集合是十分方便的，这可以用函数 PrependTo 和 AppendTo 来实现.
PrependTo[v,elem]
v 前加元素 elem
AppendTo[v,elem]
v 后加元素 elem
v={v,elem}
构造一个包含 elem 的嵌套列表
修改列表.
定义 v 的值为集合 {5,7,9}：
将 11 加到 v 中：
v 的值被改变：
AppendTo[v,elem] 是与 v=Append[v,elem] 等价的. 由于 Wolfram 系统中集合的存储方式，建立像每层长度为2的集合所组成的嵌套结构比增添一列元素更有效，当建立了这种嵌套结构后就可以用 Flatten 将其简化为一维列表.
建立一个嵌套结构 w：
用 Flatten 取消这种结构：
定义带标号的对象
在多种计算中，需要建立包含一列带标号的表达式的阵列. 在 Wolfram 语言中得到阵列的一种途径是定义列表. 你可以定义一个列表，如 a={x,y,z,…}，然后就可以用 a[[i]] 来调用它的元素或用 a[[i]]=value 来修改它. 这一方式的缺陷是必须给出它的所有元素.
定义阵列的一个简便方法是在需要时给出它的一些元素，这可以通过定义表达式如 a[i] 来实现.
定义 a[1] 的值：
定义 a[2] 的值：
显示到此为止所定义的 a 值：
即使没有给出 a[3] 和 a[4] 的值，仍然可定义 a[5] 的值：
产生 a[i] 的列表：
可以把表达式 a[i] 当作一个“带索引”或“带下标”的变量.
a[i]=value
增加变量或改动变量的值
a[i]
调用变量
a[i]=.
删除变量
?a
显示定义过的值
Clear[a]
清除定义过的值
Table[a[i],{i,1,n}]
或
Array[a,n]
转换为一个列表 List
操作带标号的变量.
在表达式 a[i] 中，i 并不一定要是整数. 事实上，Wolfram 语言允许它是任意表达式. 通过使用符号型的标号，可以在 Wolfram 语言中构造一些简单的数据库等.
具有标号 square 的对象的面积 area 为 1：
在面积 area 库中添加另一个元素：
显示到此为止的面积库 area 的元素：
在任何需要的地方都可以使用这种定义. 此处还没有定义 area[pentagon]：
定义函数
"自定义函数" 节中讨论了在 Wolfram 语言中函数的定义. 在典型情况下，可以用 f[x_]=x^2 定义一个函数 f. （事实上，在 "自定义函数" 节中用 := 而不是 = 来定义. 在 "立即定义和延时定义" 节中将解释何时使用 := 和 = ）.
定义 f[x_]=x^2 表明当 Wolfram 语言遇到与模式 f[x_] 匹配的表达式时，它将用 x^2 来代替该表达式. 由于模式f[x_] 与所有形如 f[anything] 的表达式匹配，这一定义可用于具有任何变量的函数 f.
函数定义如 f[x_]=x^2 可以与 "定义带标号的对象" 节讨论的有标号变量 f[a]=b 进行比较. 定义 f[a]=b 表明当特定 的表达式 f[a] 出现时用 b 代替. 但这定义对 f[y] 等表达式不起作用，因为这时 f 有另外的标号.
为了定义一个函数，必须给可以是任何值的变量 x 的表达式 f[x] 指定对应值，这可以通过定义模式 f[x_] 来实现，其中模式对象 x_ 代表任何表达式.
f[x]=value
对指定表达式 x 的定义
f[x_]=value
对任何涉及到 x 的表达式的定义
定有标号的变量和定义函数的区别.
定义 f[2] 或 f[a] 可以看作对阵列 f 的元素赋值. 定义一个函数 f[x_] 可以看作对一个具有任意标号的阵列的一系列元素赋值. 事实上，可以把函数看作具有任意变动标号的元素的阵列.
从数学的观点看，f 是一个映射. 当定义 f[1] 和 f[2] 等时，就是给出其定义域中离散点的象，而 f[x_] 是给出 f 在一连续流点集上的像.
对确定 的表达式 f[x] 定义变换规则：
当这一确定的表达式 f[x] 出现时，用 u 代替它. 其他表达式 f[argument] 则不变：
对任意变量定义 f 的值：
最初特定形式的 f[x] 的定义仍然有效，一般定义 f[x_] 用来求出 f[y] 的值：
清除 f 的所有定义：
Wolfram 语言允许我们对任何表达式或模式定义变换规则，可以将 f[1] 或 f[a] 等这些具体表达式的定义与像 f[x_] 等的定义相结合.
许多数学函数可以通过将特定和一般定义相结合的方式给出. 例如，阶乘函数，在 Wolfram 语言中已经给出了这一函数n!，但可以用 Wolfram 语言的定义自行建立这个函数.
阶乘函数的数学定义几乎可以直接在 Wolfram 语言中使用，其形式为 f[n_]:=n f[n-1];f[1]=1. 此定义表明对 n 等于 1 的情况，f[1] 等于 1；对其余 n，f[n] 等于 n f[n-1].
变量为 1 时阶乘函数的值：
阶乘函数一般的递推过程：
现在就可以用这个定义区得到阶乘的值乘的值：
此结果与内部函数 n! 的值相同：
定义的顺序
在 Wolfram 系统中给出一系列定义时，一部分总是比另一部分更一般一些. Wolfram 系统中的原则是：一般定义在特殊定义之后使用. 这意味着，规则的特例总是在一般情况之前试用.
这种行为对于 "定义函数" 节中给出的阶乘函数特别重要. 不管输入方式如何，Wolfram 系统总是把特殊规则 f[1] 放在 f[n_] 之前. 这意味着，当 Wolfram 系统在计算形如 f[n] 的表达式时，先测试 f[1]，当它不能用时，再使用一般情况 f[n_]. 所以，在计算 f[5] 时，Wolfram 系统将一直使用一般规则直到“终止条件” f[1] 使用了为止.
■ Wolfram 系统总是将特殊规则放在一般规则之前.
Wolfram 系统中定义的处理.
如果 Wolfram 系统不遵循上述原则，则特殊规则将会被一般规则所“屏蔽”. 在阶乘的定义中，如果规则 f[n_] 在规则f[1] 之前使用，则 Wolfram 系统即使在求 f[1] 时也会用 f[n_] 规则，而 f[1] 规则永远不会被使用.
f[n_] 的一般定义：
特殊情况 f[1] 的定义：
Wolfram 系统将特殊情形放在一般情形之前：
在像上面给出的阶乘一类的定义中，可以很明显地看出哪一个更一般一些. 但通常给出的规则没有确定的顺序，这时， Wolfram 系统就按给出的顺序使用它们.
这些规则没有明确的顺序：
Wolfram 系统按顺序保存这些规则：
log[x_y_] 的一个特例：
Wolfram 系统将特殊规则放在一般规则之前：
尽管在许多情况下，Wolfram 系统能判断哪一个规则更一般一些，但总有些例外. 例如，在两个含有 /; 的规则中，就无法确定哪一个更一般，事实上也没有明确的顺序. 在顺序不清楚时，Wolfram 系统总是按输入顺序保存规则.
立即定义和延时定义
Wolfram 语言中有两种赋值形式：lhs=rhs 和 lhs:=rhs. 其主要区别是什么时候 计算 rhs 的值. lhs=rhs 是立即赋值，即 rhs 是在赋值时立即计算. 而 lhs:=rhs 则是延时赋值，即赋值时并不计算 rhs，而是在需要 lhs 的值时才进行计算.
lhs=rhs
（立即赋值）
赋值时立即计算 rhs
lhs:=rhs
（延时赋值）
每次需要 lhs 时计算 rhs
Wolfram 语言中的两种赋值形式.
用 := 定义函数 ex：
由于使用了 :=，该定义中仍然保持没有计算之前的形式：
使用 = 赋值时，右端立即被计算出来：
现在保存的定义是 Expand 命令的结果：
当执行 ex 时，就调用 Expand：
iex 将它的变量替换到已展开的形式中去，给出不同形式的结果：
从上面的例子看出， = 和 := 都可以用来定义函数，要特别注意它们的差异.
一个常用的原则是：当一个表达式的值再不改变时用 =，而通过赋值求表达式的一个值时用 :=. 在无法确定时用 := 总比用= 好一些.
lhs=rhs
rhs 是 lhs 的永久值 （如 f[x_]=1-x^2）
lhs:=rhs
rhs 给出了需要 lhs 的值时执行的一个指令，（如f[x_]:=Expand[1-x^2]）
用 = 和 := 赋值的含意.
尽管 := 比 = 用得多一些，但还有必须用 = 定义函数的一个重要情形. 当进行一个运算得到具有符号参数 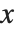的结果时，还需要进一步得到对应于不同 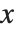的结果. 一种方式是用 /. 将适当的规则用于 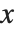. 通常用 = 去定义变量 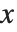的函数就较方便一些.
涉及 x 的一个表达式：
定义一个自变量可用 x 的值代入的函数：
x 为 1+a 时的结果：
上面例子中值得注意的一点是在模式 x_ 中出现的名称 x 没有任何特殊支持，它仅是一个符号，与其他表达式中出现的 x 没有区别.
f[x_]=expr
对任何指定的 x 值，函数的值为 expr
定义表达式值的函数.
= 和 := 不仅用来定义函数，还用来给变量赋值. x=value 立即求 value 的值，并将其赋于 x. 另一方面，x:=value 不立即求值 value. 而是在每次使用 时才计算其值.
计算 RandomReal[] 求出一个伪随机数，赋给 r1：
这里 RandomReal[] 先不计算，在每次使用 r2 时进行计算：
此处给出 r1 和 r2 的值：
r1 的值维持不动，每次使用 r2 时，就产生一个伪随机数：
在一系列值语句中，要特别注意立即赋值和延时赋值的区别.
令 a 等于 1：
这里计算 a+2 得到 3，将结果赋于 ri：
这里 a+2 先不计算，等到 rd 使用时求其值：
此处 ri 和 rd 值相同：
此时 a 的值被改变：
现在 rd 使用 a 的新值，而 ri 保持不动：
可以用延时赋值 t:=rhs 来设置在不同环境下有不同值的变量. 当每次需要 t 的值时，就用与 rhs 有关变量的当前值来计算它的值.
延时赋值的右端暂不计算：
令 a 等于 4，再求出 t 的值：
这里令 a 等于6：
在上面的例子中，符号 a 是一个全局变量，它的值决定了 t 的大小. 当参数中大部分偶尔才变化时，用这种方式是方便的. 但必须认识到明显的或隐含的变量之间的依赖关系是容易混淆的，应该尽可能地使用函数明确地反映依赖关系.
lhs->rhs
给出规则后就计算 rhs
lhs:>rhs
使用规则时计算 rhs
Wolfram 语言中的两种变换规则.
与 Wolfram 语言中的立即或延时赋值类似，可以建立立即或延时的变换规则.
给出规则时其左端立即计算：
这类规则不一定十分有用：
规则的右端暂不计算，每次使用规则时才求它的值：
使用规则时就进行展开：
与赋值的情形类似，当用确定的值代替表达式的值时用 ->，而当给出一个求值的命令时用 :>.
保留已有值的函数
用 := 定义的函数中，调用是函数的值就会被反复计算. 但一些计算中，需要将同一组函数使用多次，这时就可以让 Wolfram 语言记住这些函数值以节省时间. 接下来就给出定义这种函数的方法.
f[x_]:=f[x]=rhs
定义一个保存已有值的函数
定义保存已有值的函数.
定义一个函数 f，它保存所有已得到的值：
此处给出 f 递推结束的条件：
f 已有的定义：
求 f[5] 时，需要计算 f[5]，f[4]，… f[2]：
到此为止的 f 值全部保存着：
此时再求 f[5] 时，Wolfram 语言可立即找出，不需要重新计算：
用户可以看到定义如 f[x_]:=f[x]=f[x-1]+f[x-2] 是如何工作的. 函数 f[x_] 被定义为这个“程序” f[x]=f[x-1]+f[x-2]. 当调用函数 f 的值时，执行该“程序”. 该程序首先计算 f[x-1]+f[x-2]，再将结果保存到 f[x] 中.
在 Wolfram 语言中进行递推运算时，使用能保存已有值的函数是一个好方法. 递推的一个典型情况是函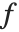数 在整数 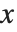的值通过它在 、 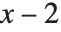等值给出. Fibonacci 函数定义 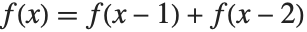就是这样的一种递推，在计算 时，需反复递推，如需要反复计算 多次，故此时记住 的值下次直接找出就比反复计算要好.
关于记住函数值，这里存在一个权衡. 在记住了一些函数值时，查找就比计算快，但这需要占用内存. 通常当重复计算的代价很大时保存函数值，且需要保存的函数不宜太多.
将定义与不同的符号相关联
在 Wolfram 语言中，f[args]=rhs 或 f[args]:=rhs 会将对象 f 和你的定义相关联. 也就是说，当输入 ?f 时，就会显示该定义. 一般我们把符号 f 作为标头的表达式称为 f 的下值 (downvalue).
Wolfram 语言也支持上值 (upvalue)，上值可以把不直接作为标头的符号与定义相关联.
比如，在定义 Exp[g[x_]]:=rhs 中，一种可能是把定义与符号 Exp 相关联，认为它是 Exp 的下值. 但是从组织或效率的角度来看未必是最好的方式.
较好的方式是将 Exp[g[x_]]:=rhs 与 g 关联起来，即对应为 g 的上值.
f[args]:=rhs
定义 f 的下值
f[g[args],…]^:=rhs
定义 g 的上值
把定义与不同符号相关联.
定义 f 的下值：
查看 f 的定义：
定义 g 的上值：
此定义与 g 相关联：
此定义不与 Exp 相关联：
用此定义求表达式的值：
在简单的情况下，无论你是将 f[g[x]] 的定义作为 f 的下值或 g 的上值，计算结果都是一样的. 然而，其中一个比另一个更自然或更有效一些.
一般的原则是，当函数 f 比 g 更常用的时，f[g[x]] 的定义应该作为 g 的上值. 因此，例如，在 Exp[g[x]] 中，Exp 是 Wolfram 语言中的内部函数，g 是引入的一个函数，此时将 Exp[g[x]] 作为 g 的上值，而不是 Exp 的下值，会更合理和自然.
定义 g 的上值：
目前，g 的定义：
只要可能，就会使用 g 的和这个定义：
由于模式 g[x_]+g[y_] 的完全形式是 Plus[g[x_],g[y_]]，该模式的定义可以作为 Plus 的下值，然而将它看作 g 的上值会更好一些.
一般来说，当 Wolfram 语言遇到一个特定函数时，它会尝试所有已给出的该函数的定义. 如果把 g[x_]+g[y_] 定义为 Plus 的下值时，则当遇到 Plus 时，Wolfram 语言就会试用这个定义. 这样，当每次 Wolfram 语言遇到加法时都会测试这个定义，因此使得运行速度变慢.
然而，当把 g[x_]+g[y_] 的定义作为 g 的上值时，你把定义与 g 关联. 仅当 g 出现在函数，例如 Plus 内时才尝试这个定义. 因为 g 出现的频率比 Plus 出现的少，因此这个是更有效的进程.
f[g]^=value
或
f[g[args]]^=value
让赋值与 g 相关联而不是与 f 相关联
f[g]^:=value
或
f[g[args]]^:=value
让延迟赋值与 g 相关联
f[arg1,arg2,…]^=value
让赋值与所有 argi 的标头相关联
定义上值的更简洁的方法.
上值的典型用法是建立特定对象的属性“数据库”，使用上值可以把对象的定义与所关心的相关联，而不是与你指定的属性相关联.
定义 square 的上值给出其面积：
加入周长的定义：
这两个定义都与 square 对象相关联：
一般可以将一个表达式的定义和出现在表达式中足够高层次的任何符号相关联. 在形如 f[args] 的表达式中，只要 g 本身或以 g 为标头的对象出现在 args 中时，就可以定义符号 g 的上值. 但当 g 出现在表达式的较低层次中时，就无法将这些定义与它相关联.
g 是变量的标头，可以使其与该定义相关联：
g 在左端出现的层次太低，故无法将它与定义相关联：
f[…]:=rhs
f 的下值
f/:f[g[…]][…]:=rhs
f 的下值
g/:f[…,g,…]:=rhs
g 的上值
g/:f[…,g[…],…]:=rhs
g 的上值
定义中符号的可能位置.
如 "表达式的含义" 中描述的，在 Wolfram 语言中，符号可作为“标记”来表明表达式的“类型”. 例如，复数在 Wolfram 语言中的内部形式为 Complex[x,y]，这里符号 Complex 表明此对象是一个复数.
上值提供了一个运算和标记的简便方法. 例如，当需要引入类型为 quat 的一组抽象对象时，就可以用 quat[data] 形式的 Wolfram 语言表达式来表示这个类型的每一个对象.
典型的情况是，你可能想让 quat 对象有加法和乘法等算术运算的性质，这可以通过定义 quat 关于 Plus 和 Times 的上值来实现.
定义 quat 关于 Plus 的上值：
刚定义的上值用来简化这一表达式：
当定义 quat 关于 Plus 运算的上值时，就是扩大 Plus 的运算域以便包括 quat，即告诉 Wolfram 语言使用特殊的加法规则，当 quat 对象被加在一起时，它们仍是 quat 对象.
在定义 quat 对象的加法时，可以总是有特殊的加法操作，例如 quatPlus，你可以对其赋予合适的下值. 但用 Wolfram 语言中的标准运算 Plus 来表示加法，当遇到 quat 对象时，通过指定特殊行为来“覆盖”该操作，会更方便一些.
可以将上值看作实现一些面向对象编程功能的一种途径. 符号像 quat 表示一类特殊的对象类型，quat 的各种上值指定“方式”，其定义 quat 对象在某种运算中应如何操作或接收哪种“消息”.
定义数量值
在定义如 f[x_]:=value 中，Wolfram 语言的值将被赋给所有的函数 f. 但有时需要定义一个求值时才使用的值.
expr=value
定义一个任何情况下都用的量
N[expr]=value
定义一个用作近似值的量
定义普通值和数量值.
定义 f 的一个数量值：
定义数量值不影响 f 的其他值：
进行近似计算时使用刚才的数量值：
对函数和符号都可以定义数量值，NIntegrate 和 FindRoot 等数值函数都可以使用数量值.
N[expr]=value
定义默认精度的数量值
N[expr,{n,Infinity}]=value
定义有 n 位精度的数量值
定义与精度有关的数量值.
定义符号 const 的数量值，在求积中使用 4n+5 项，并具有 n 位精度：
有30位精度的 const 的值：
在 Wolfram 语言中，数量值的处理与上值类似，当定义了 f 的数量值以后，Wolfram 语言就象求值运算 N 中 f 的上值一样来输入这一定义.
修改内置函数
在 Wolfram 语言中可以对任何表达式定义变换规则. 不仅可以定义添加到 Wolfram 语言中的函数，而且还可以对 Wolfram 语言的内置函数进行变换，于是就可以增强或修改内置函数的功能.
这一功能是强大的，同时也具有潜在的危险. Wolfram 语言永远遵循给出的规则，当规则不正确时，就会得出错误的结果.
为了避免在修改内置函数过程中的错误，Wolfram 语言限制对内置函数重新定义. 当要定义内置函数时，首先要去掉这种限制. 完成定义以后要恢复这一限制以免以后犯错误.
Unprotect[f]
去掉保护限制
Protect[f]
加上保护限制
函数的保护.
内置函数通常被“保护”，不能重新定义它们：
去掉 Log 的保护：
现在可以自行定义 Log 函数. 即使这个定义不正确，Wolfram 语言也允许你这样定义：
不论这个定义正确与否，Wolfram 语言将在所有可能的情况下使用用户的定义：
清除 Log 的不正确定义：
恢复对 Log 的保护：
用户定义的函数高于 Wolfram 语言内置函数. 一般说来，Wolfram 语言总是先使用用户定义的函数.
Wolfram 语言的内置规则是希望能进行宽广的各种运算. 在有些不愿意用内置规则的情况下，可以用可以定义的规则来超越内置的规则.
简化 Exp[Log[expr]] 时有一个内置规则：
可以自行定义 Exp[Log[expr]] 来代替内置规则：
现在使用了自己的定义，而不是内置规则：
值集的操作
DownValues[f]
给出 f 的下值集
UpValues[f]
给出 f 的上值集
DownValues[f]=rules
建立 f 的下值
UpValues[f]=rules
建立 f 的上值
建立和寻找符号的值.
Wolfram 语言按变换规则列表的方式有效地保存给出的定义. 当遇到一个符号时，就调用与它有关的规则列表.
在绝大部分情况下，不需要涉及与定义有关的变换规则，只需要用 lhs=rhs 和 lhs=. 来添加或删除规则. 然而，在有些情况下，直接进入这些规则是十分有用的.
定义 f：
对 f 定义清晰的规则：
注意，建立 DownValues 和 UpValues 的返回值规则是为了让左、右两边都不进行计算. 左端包含在 HoldPattern 中，规则被延时，所以右边不立即计算.
正如在 "定义函数" 中讨论的一样，Wolfram 语言按特殊定义出现在一般定义之前的原则对定义排序. 但事实上，没有唯一确定的方式去排序，可以用与 Wolfram 语言默认次序不同的方式去排序，对用 DownValues 和 UpValues 得到的规则表重新排序就达到目的.
下面是对象 g 的一些定义：
这里显示了定义的默认顺序：
这里对 g 定义的顺序进行反向：