ベクトル解析

直交座標系でのベクトル解析直交座標系以外の座標系でのベクトル解析
ベクトル解析は多数の物理および数学モデルの基礎をなす．Wolfram言語はさまざまな座標系で傾き，発散，回転，ラプラシアンの基本的な操作を計算することができる．さらに，これらの演算子は非常に一般的な形式で実装されているので，いろいろな次元で使うことも，高階のテンソルで使うこともできる．
直交座標系でのベクトル解析

ベクトル導関数

以下の表に，基本的な4つのベクトル導関数を示す．
Grad[f,{x1,…,xn}]
スカラー関数の傾き
Div[{f1,…,fn},{x1,…,xn}]
ベクトル値関数 の発散
Curl[{f1,…,fn},{x1,…,xn}]
ベクトル値関数の回転
Laplacian[f,{x1,…,xn}]
スカラー関数 のラプラシアン
直交座標系におけるベクトル導関数の一般的な演算子．
上記の演算子は何次元で使うこともできるが，ほとんどの場合は三次元で見ることが多い．
三次元の傾きを与える：
三次元の発散を計算する：
三次元での回転はベクトルを返す：
次はラプラシアンを三次元空間で返す：
以下は，これらの演算子を三次元以外で使った例である．
二次元の傾きを与える：
ベクトルの発散は，どの次元でもスカラーである：
五次元のラプラシアンを計算する：
回転は三次元に限られない．次は，スカラーである二次元回転を与える：
より一般的に言うと， 次元のベクトルの回転は階数 の完全反対称テンソルである：
三次元以外での回転の意味は，次のサブセクションで詳しく説明する．

高階テンソルへの一般化

前セクションで紹介した4つの演算子はすべて，入力としてベクトルや高階のテンソルを取ることのできる一般的な演算子である．次元 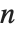のCurlでは，入力はスカラー，ベクトル，階までのテンソルが取れる．他の関数では，入力テンソルで取れる階数には制約がない．
ベクトルの傾きは二階テンソルである．傾きが増えるごとに階数が1増える：
発散は，最後の2つのスロットの縮約が後続する傾きである．したがって階数は1減る：
TensorContractを使うと，最後のスロット以外のスロットにおける発散が取れる：
ラプラシアンは階数を保存するので，ベクトルのラプラシアンは別のベクトルになる：
次元が の場合，階数 のテンソルの回転は階数 のテンソルである：
このようになる理由は，回転が反対称の傾きのホッジ双対となっているためである．これにより階数に対する制約も説明が付く：
直交座標系以外の座標系でのベクトル解析

既知の座標チャート

Wolfram言語には，多数の座標チャートに関する情報が含まれている．関数CoordinateChartDataはこの情報を取得するためのメカニズムを提供する．
CoordinateChartData[{"coordsys",n}]
次元のユークリッドチャートに対する標準的な名前
CoordinateChartData[{All,n}]
次元のユークリッド空間で利用できる座標チャート
CoordinateChartData[{All,All,n}]
次元空間で利用できる座標チャート
CoordinateChartData[chart,"prop"]
指定された座標チャートの特性 "prop"
CoordinateChartData[chart,"prop",pt]
点 pt において指定された座標チャートの特性 "prop"
座標チャートに関する情報
以下は利用できる座標チャートを調べる方法を説明した例である．もっとも一般的な形式では，座標チャートの指定には座標系の名前，計量，次元が含まれる．多くのチャートでパラメータも必要とされる．これらは指定することもできるし，デフォルトのままにすることもできる．
次はWolfram言語に三次元直交座標系の標準名を与える：
扁長楕円体座標系は，焦点距離の半分というパラメータを取る：
パラメータは入力で指定することができる：
複数のパラメータが指定される場合は，リストで囲まなければならない：
以下は二次元ユークリッド空間で利用できる座標チャートである：
上の入力をより明示的に表したのが下である：
計量"Euclidean"をシンボルAllで置き換えると，ユークリッド座標でないチャートが含まれる：
座標チャートの標準名はかなり長いが，ユークリッド座標チャートを使うときは"Euclidean"と次元を省略することができる．
CoordinateChartDataは異なる座標チャートに関する多数の特性を含んでいる．もっとも基本となるのが計量である．これは最終的に座標チャートすべての長さと体積を決定する．しかし，直交座標系におけるベクトル解析においては，スケール因子と体積因子を考える方が一般的である．
以下は点における極座標系の計量を得る：
対角計量の場合，スケール因子は対角項目の平方根である：
体積因子は，計量の決定因子の平方根である：
次は回転に沿った楕円座標のスケール因子を与える．ここではデフォルトパラメータの が使われている：
スケール因子は座標速度 と物理的速度を関連付ける：
物理的速度が速度のノルムになった．これは計量と座標速度から直接得ることもできた：
次はパラメータが1に設定された双極座標系の体積因子を与える．1が次元ではなくパラメータとして扱われるようにするために，二重のリストが必要である：
対角計量の場合，体積因子はスケール因子の積である：
次は双極座標系の座標環の物理的面積を与える：
次のシンタックスを使うと，利用できる特性すべてが見付かる：

直交座標系以外の座標系でのベクトル導関数

4つのベクトル導関数演算子は，どの座標チャートでも使える．関数の第3引数でチャートを指定することだけが必要となる．
Grad[f,{x1,…,xn},chart]
指定された座標チャートにおける傾き
Div[{f1,…,fn},{x1,…,xn},chart]
指定された座標チャートにおける発散
Curl[{f1,…,fn},{x1,…,xn},chart]
指定された座標チャートにおける回転
Laplacian[f,{x1,…,xn},chart]
指定された座標チャートにおけるラプラシアン
直交座標系以外の座標系でのベクトル解析演算子．
これらのコマンドにおける配列は，正規直交基底における要素として扱われる．これは入出力の両方に当てはまる．その結果，物理的なドット積はDotを使って計算できる．
直交座標では，スカラーの傾きは偏導関数をスケール因子で割ったものに等しい：
ベクトルおよび高階テンソルの傾きは結果との接続項を導入する．つまり，これは単に各要素の傾きではないということである：
発散はベクトルとテンソルにだけ当てはまるので，常に接続項を持つ．しかし，配列は正規直交基底にあるものとして扱われるため，発散はまだ縮約が後続する傾きである：
接続項があるため，二階テンソルの発散は単に各項の発散というわけではない：
定義では，ラプラシアンは傾きの発散である．その結果，ラプラシアンは直交座標以外の座標でも接続項を持つ：
つまり，ベクトルラプラシアンは単に各要素のラプラシアンではないということである：
ベクトルと高階のテンソルに作用すると，回転も接続項を含む：
スカラーに作用すると，接続項はないが，スケール因子からの正規化が結果に現れる：

従来の定義

前述のように，直交座標系におけるスカラーの傾きには，偏導関数とスケール因子が含まれる．スケール因子および体積因子に関するベクトルの発散，スカラーのラプラシアン，ベクトルの回転にも同様の定義がある．
直交チャートの傾きはスケール因子により直交座標系の傾きと関連している：
直交座標系では，ベクトルの発散の従来の公式は，スケール因子と体積因子を使って直交座標系の発散と関連付けられている：
発散の従来の公式と直交座標系におけるスカラーの傾きの定義を組み合せると，ラプラシアンの従来の公式ができる：
次は，ベクトルの三次元回転に対する同様の公式を説明するものである．次元 に一般化するためには，先頭の scales を 個のscalesのTensorProductで置換する．